因果推断——借微软EconML测试用DML和deepIV进行反事实预测实验（二十五）

Posted 2022-02-04 悟乙己

文章目录

• 1 导言
• • 1.1 KDD2021：盒马-融合反事实预测与MDP模型的清滞销定价算法
  • 1.2 本篇想法
• 2 代码
• • 2.1 数据生成
  • 2.2 DML模型：有干预下的Y增量
  • 2.3 Tree-based模型
  • 2.4 deepIV训练与预测
  • 2.5 结果比较
  • 2.6 短期小结

---

1 导言

1.1 KDD2021：盒马-融合反事实预测与MDP模型的清滞销定价算法

本篇想法来源：因果推断与反事实预测——盒马KDD2021的一篇论文（二十三）
盒马论文提到了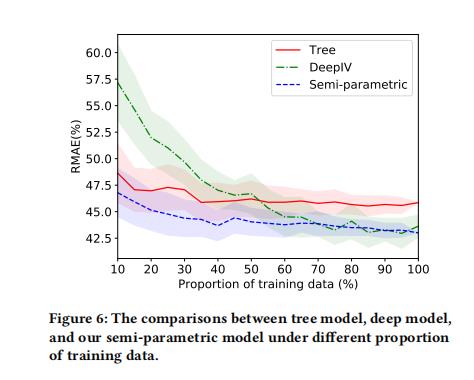

• 论文模型：半参数模型，上图是顺着使用数据的比例增加三个模型的RMAE，
• 对比方案1-XGB：将折扣Treatment作为特征放入模型中预估销量值，但是这个模型本身存在混杂因子，估计是有偏的；
• 对比方案2-DeepIV：将三级品类的平均价格（treatment）作为工具变量，建模深度学习模型刻画折扣和销量的关系，其中折扣Treatment建模成高斯分布

其中主结构模型为：

$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=g(d_i;L_i,\theta )+h(d_i^{\text{o}},x_i)-g(d_i^{\text{o}};L_i,\theta )$

函数$h(d_i^{\text{o}},x_i)$为非参数预测模型，用于预测某个商品平均折扣$d_i^{\text{o}}$下的销量，
如果$d_i=d_i^{\text{o}}$，那么
$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})|d_i^{\text{o}}]=h(d_i^{\text{o}},x_i)$
如果$d_i!=d_i^{\text{o}}$，那么$g(d_i)-g(d_i^{\text{o}})$代表的是，特别折扣下的增量（新折扣增量），所以通俗来说就是：
$\mathbb{E}[\ln (Y_i/Y_i^{\text{nor}})]=平均折扣销(predict-model）+特殊折扣增量(price-elasticity)$

• $Y_i^{\text{o}}$是常规渠道产品$i$近期的平均销量
• $d_i^{\text{o}}$是商品$i$近期的平均折扣
• $Y_i/Y_i^{\text{nor}}$代表了折扣价格使得销量增加的百分比，因为不同商品销量差异很大，所以比率会比绝对值更有用
• 函数$g(d_i;L_i,\theta )$是参数化的价格弹性模型，参数$\theta \in {\mathbb{R}}^{m+1}$

1.2 本篇想法

其中关于盒马那篇文章提到的半参数模型，思路上有一些启发，这里就自己沿着他们的思路DIY一下，借用微软开源的EconML来实现，让我来快速介绍一下本篇会尝试几种思路。
X-协变量Covariates；Y-Responses；W-混淆因子；T-干预treatment

• 实验测试模型1：Tree模型，将T(干预treatment)作为特征直接加到模型里面，也就是此时没有T/W/X，都是自变量，直接使用最简单的XGBoost
• 实验测试模型2：将T作为IV，与盒马一样，借由Econml开源的deepIV
• 实验测试模型3：本篇比较想尝试的，分为两个：
  • 无干预样本（T=0）：Tree-based模型$E(y|x,w)$
  • 有干预样本（T=1）：Tree-based模型$E(y|x,w)+DML(Y|X,W,T)$

这里针对模型3，解释一下：

• Tree-based模型$E(y|x,w)$，与模型1不同，这里没有把干预T作为特征放进去，而是只筛选了T=0的情况，然后根据T=0情况下的样本进行训练，那么这个模型就代表没有干预的情况下，正常X|W会有多少销量Y（类似盒马论文中的$h(d_i^{\text{o}},x_i)$为非参数预测模型，用于预测某个商品平均折扣$d_i^{\text{o}}$下的销量）
• $DML(Y|X,W,T)$这里指的是，利用DML来求在X|W特定情况下，有干预的情况下的异质性处理效应CATE，那么这个CATE代表的是，有干预下的弹性增量

所以这里 ： Tree-based模型$E(y|x,w)+DML(Y|X,W,T)$，大概的反事实预测思路是，

Y的预测值 = 无干预下的Y预测值 + 有干预下的Y增量

当然盒马那里提出了价格弹性，而且品类非常细分，本篇没那么细致的数据就先不考虑这种方式。

---

2 代码

2.1 数据生成

这里很简单粗暴跟着Econml里面的代码来生成数据，只是实验，不太严谨。。

笔者使用的软件版本：

econml.__version__,keras.__version__,xgboost.__version__
>>> ('0.12.0', '2.6.0', '1.3.3')

数据生成：

import econml

## Ignore warnings
import warnings
warnings.filterwarnings("ignore")

# Main imports
from econml.dml import DML, LinearDML, SparseLinearDML, CausalForestDML

# Helper imports
import numpy as np
from itertools import product
from sklearn.linear_model import (Lasso, LassoCV, LogisticRegression,
                                  LogisticRegressionCV,LinearRegression,
                                  MultiTaskElasticNet,MultiTaskElasticNetCV)
from sklearn.ensemble import RandomForestRegressor,RandomForestClassifier
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
import matplotlib
from sklearn.model_selection import train_test_split

%matplotlib inline

# Treatment effect function
def exp_te(x):
    return np.exp(2 * x[0])# DGP constants

np.random.seed(123)
n = 2000
n_w = 30
support_size = 4
n_x = 6
# Outcome support
support_Y = np.random.choice(range(n_w), size=support_size, replace=False)
coefs_Y = np.random.uniform(0, 1, size=support_size)
epsilon_sample = lambda n:np.random.uniform(-1, 1, size=n)
# Treatment support
support_T = support_Y
coefs_T = np.random.uniform(0, 1, size=support_size)
eta_sample = lambda n: np.random.uniform(-1, 1, size=n) 

# Generate controls, covariates, treatments and outcomes
W = np.random.normal(0, 1, size=(n, n_w))
X = np.random.uniform(0, 1, size=(n, n_x))
# Heterogeneous treatment effects
TE = np.array([exp_te(x_i) for x_i in X])
# Define treatment
log_odds = np.dot(W[:, support_T], coefs_T) + eta_sample(n)
T_sigmoid = 1/(1 + np.exp(-log_odds))
T = np.array([np.random.binomial(1, p) for p in T_sigmoid])
# Define the outcome
Y = TE * T + np.dot(W[:, support_Y], coefs_Y) + epsilon_sample(n)

# 生成训练数据
Y_train, Y_val, T_train, T_val, X_train, X_val, W_train, W_val = train_test_split(Y, T, X, W, test_size=.2)
# Generate test data
#X_test = np.array(list(product(np.arange(0, 1, 0.01), repeat=n_x)))

W.shape,T.shape,X.shape,Y.shape#,X_test.shape
>>> ((2000, 30), (2000), (2000, 6), (2000)) 

这里的混淆因子W有30个维度，T为0/1变量，X为6维特征

2.2 DML模型：有干预下的Y增量

参考的：
因果推断笔记——DML ：Double Machine Learning案例学习（十六）

这里测试了四款DML模型：
LinearDML；SparseLinearDML；DML；CausalForestDML

# Default Setting
est = LinearDML(model_y=RandomForestRegressor(),
                model_t=RandomForestRegressor(),
                random_state=123)
est.fit(Y_train, T_train, X=X_train, W=W_train,cache_values = True)
#te_pred = est.effect(X_test)
print('LinearDML')

# fit(Y, T, X=X, W=W,

# Polynomial Features for Heterogeneity
est1 = SparseLinearDML(model_y=RandomForestRegressor(),
                       model_t=RandomForestRegressor(),
                       featurizer=PolynomialFeatures(degree=3),
                       random_state=123)
est1.fit(Y_train, T_train, X=X_train, W=W_train)
#te_pred1 = est1.effect(X_test)
print('SparseLinearDML')

# Polynomial Features with regularization
est2 = DML(model_y=RandomForestRegressor(),
           model_t=RandomForestRegressor(),
           model_final=Lasso(alpha=0.1, fit_intercept=False),
           featurizer=PolynomialFeatures(degree=10),
           random_state=123)
est2.fit(Y_train, T_train, X=X_train, W=W_train)
#te_pred2 = est2.effect(X_test)
print('DML')

# CausalForestDML
est3 = CausalForestDML(model_y=RandomForestRegressor(),
                       model_t=RandomForestRegressor(),
                       criterion='mse', n_estimators=1000,
                       min_impurity_decrease=0.001,
                       random_state=123)
est3.tune(Y_train, T_train, X=X_train, W=W_train)
est3.fit(Y_train, T_train, X=X_train, W=W_train)
#te_pred3 = est3.effect(X_test)
print('CausalForestDML')

2.3 Tree-based模型

这里干预Tree-based模型，有两个，也就是1.2里面说的，

• 测试模型1，需要W,X,T都作为解释变量；
• 测试模型3，需要W,X作为解释变量且干预=0的样本

import xgboost
#import shap
import numpy as np
#shap.initjs()
import numpy as np
import pandas as pd
from sklearn import preprocessing
import lightgbm as lgb

from sklearn.metrics import mean_squared_error # 均方误差
from sklearn.metrics import mean_absolute_error # 平方绝对误差
from sklearn.metrics import r2_score # R square

# 测试模型3，只筛选T=0的样本
Y_train_2 = np.array([Y_train[n]  for n,i in enumerate(T_train) if i ==0  ] )
T_train_2 = np.array([T_train[n]  for n,i in enumerate(T_train) if i ==0  ] )
if X_train.shape[1] == 1:
    X_train_2 = np.array([X_train[n]  for n,i in enumerate(T_train) if i ==0  ] ).reshape((-1,1))
else:
    X_train_2 = np.array([X_train[n]  for n,i in enumerate(T_train) if i ==0  ] )#.reshape((-1,1))
W_train_2 = np.array([W_train[n]  for n,i in enumerate(T_train) if i ==0  ] )#.reshape((-1,1))

# 训练集
XW_train_0 = np.hstack((X_train_2,W_train_2)) # 测试模型3-只有干预=0的样本
XW_train_0_1 = np.hstack((X_train,W_train))  
XWT_train_0_1 = np.hstack((XW_train_0_1,T_train.reshape((-1,1)))) # 测试模型1-W,X,T都作为特征的训练集

# 生成验证集
XW_val = np.hstack((X_val,W_val))  # 测试数据集
XWT_Val = np.hstack((XW_val,T_val.reshape((-1,1)))) # 测试数据集

以上就是训练、验证数据的生成过程

然后就是非常简单的训练与预测的过程：

# 测试模型3-只有T=0的情况下
model_0 = xgboost.XGBRegressor().fit(XW_train_0, Y_train_2)

# 测试模型1-xwt模型 - 都包括
model_01 = xgboost.XGBRegressor().fit(XWT_train_0_1, Y_train)

# 测试模型3-只有T=0的情况下- 验证
以上是关于因果推断——借微软EconML测试用DML和deepIV进行反事实预测实验（二十五）的主要内容，如果未能解决你的问题，请参考以下文章
 
 因果推断笔记——因果图建模之微软开源的EconML
 因果推断笔记——因果图建模之微软开源的EconML
 因果推断笔记——工具变量内生性以及DeepIV
 因果推断笔记——工具变量内生性以及DeepIV
 因果推断笔记——DML ：Double Machine Learning案例学习（十六）
 因果推断笔记——DML ：Double Machine Learning案例学习（十六）