因果推断笔记—— 相关理论：Rubin PotentialPearl倾向性得分与机器学习异同

Posted 悟乙己

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了因果推断笔记—— 相关理论：Rubin PotentialPearl倾向性得分与机器学习异同相关的知识，希望对你有一定的参考价值。

文章目录

1 一些因果推断涉及概念

1.0 因果推断的几个境界

《Theoretical Impediments to Machine Learning With Seven Sparks from the Causal Revolution》这篇论文说到了因果推断的三层。

原论文：
http://arxiv.org/abs/1801.04016

  • 第一层是关联：纯粹的统计关系，X条件下Y会怎么样，也就是现在机器学习中常用的方式，尽可能通过深层次的网络去拟合X和Y的关系
    观察一个购买牙膏的顾客，那么他/她购买牙线的可能性更大;这种关联可以使用条件期望直接从观察到的数据推断得出
  • 第二层是干预：新的冲击下，两者的关联关系 ；这个层次的一个典型问题是：如果我们将价格翻倍会怎样？这些问题无法单独从销售数据中得到解答，因为它们涉及客户响应新的定价的行为的变化。
  • 第三层是反事实推断：相当于对结果来考虑原因，相当于如果我们希望Y变化，那么我们需要对X做出什么样的改变？（下面贴原文，其实蛮费解的。。）

个人观点：因果推断可以补充机器学习方法过程中没有解释清楚的问题，一般ML都是解释X-> Y，但是没有说明白 Y-> X。

本节参考：
论文学习笔记1——《机器学习的理论局限与因果革命的7大火花》（因果推理必将带来现有人工智能领域研究的再一次巨大突破）
因果推断综述及基础方法介绍（一）

1.1 内生性问题

1.1.1 内生性解释

参考：金融学里的内生性和外生性是什么意思？

经典的多元回归模型开始，下面给出4个基础假定。

  • 假定1：线性关系假定，被解释变量与解释变量存在线性随机函数关系。
  • 假定2：严格外生假定。
  • 假定3：球形扰动假定。
  • 假定4：无完全共线假定，解释变量之间无完全共线性。
    假定2 的文字表述是“当所有时期的解释变量X给定时，每一期的随机干扰项均值都为 0”，外生性假定不满足，这便产生了内生性问题。严格来说，若扰动项与解释变量不满足弱外生性假定，我们称模型存在内生性问题，与扰动项相关的解释变量被称为内生变量

1.1.2 内生性问题有四种常见形式

内生性！内生性！解决方法大集合

  • 1.遗漏解释变量X。研究者通常无法控制所有能影响被解释变量的变量，因此遗漏解释变量 (omitted variables) 是很常见的事情。如果遗漏的变量 X2对另一个解释变量 X1有影响，就会产生内生性问题。

  • 2.X与Y互为因果，有时也称反向因果关系。

  • 3.选择偏差,选择偏差包括两种形式，即样本选择偏差 (sample selection bias) 和自选择偏差 (self-selection bias);样本选择偏差是指因样本选择的非随机性导致结论存在偏差，本质上也是一种遗漏变量问题 (Heckman，1979)。

  • 4.测量误差问题,当模型使用数据和真实数据存在误差，且满足 CEV 假定时，则会影响估计量的一致性，产生内生性问题。当只有一个解释变量时，CEV 假定下的测量误差将导致 OLS 估计量产生向 0 的偏误，也称为衰减偏误。当模型存在多个解释变量时，其中一个解释变量的测量误差导致 OLS 估计量发生方向不确定的偏移。

1.1.3 内生性的解决方案

1.自然实验法——随机实验

所谓自然实验，就是发生了某些外部突发事件，使得研究对象仿佛被随机分成了实验组或控制组。这是我最喜欢的方法，只是自然实验需要寻找一个事件，并且这个事件只影响解释变量而不影响被解释变量。遇着这种事件是一种缘分，还要能识别出来，这对学者的眼光也是一种挑战。

2.双重差分法Difference-in-Difference （DID）

因果推断综述及基础方法介绍（一）

这张图讲得非常清楚，首先为什么我们不能用ATE = E(Yi|Ti=1)−E(Yi|Ti=0)，举个 ，我们给一些人发权益，另一些人不发，我们怎么能知道权益带来的购买效果是怎么样的呢？简单的方法就是给发权益的人购买数加和，不发权益的人购买数加和，然后两个加和相减就好啦，但是如果这两部分人本来不发权益的时候购买数就不一样呢？

那就减两次，从上图来说，我们把这两群人发权益之前t0的购买数相减，得到一个差值，相当于这两群人的固有差距，再把这两群人发权益之后t1的购买数相减，相当于这两群人被权益影响之后的差距，后面的差距减去前面的差距，就会得到权益对于差距有多少提升（降低），以此作为权益的effect。

这个方法的问题在于有个比较强的要求是，趋势平行，也就是要求t0到t1之间，两群人的购买概率变化趋势是一样的（图中那个平行线），这其实是一个很强的假设，所以这个方法我个人来讲不算非常认可。

3.工具变量法

有哪些有趣的工具变量?

这是一种处理内生性问题的经典方法，或者说被滥用最严重的方法。这种方法相信大家都已经学过，就是找到一个变量和内生解释变量相关，但是和随机扰动项不相关。
在OLS的框架下同时有多个工具变量（IV），这些工具变量被称为two stage least squares (2SLS) estimator。具体的说，这种方法是找到影响内生变量的外生变量，连同其他已有的外生变量一起回归，得到内生变量的估计值，以此作为IV，放到原来的回归方程中进行回归。

工具变量法最大的问题是满足研究条件的工具变量难以找到，而不合乎条件的工具变量只能带来更严重的估计问题。

这里借用连玉君 的讲义

王小二参加研究生复试的面试时，恰好认识其中一位参加面试的老师。假设面试分数 (Y) 由面试老师 (X) 决定，王小二可视为随机误差项u ，认识王小二的那位面试老师可视为内生的解释变量x1 ，如果让这位老师继续参加面试给王小二打分，那么面试分数就很可能偏高。

如何解决这个内生性问题呢？不妨再找另一个老师来代替这位跟王小二认识的老师，基本要求是：新找来的老师不能跟王小二认识，并且又跟被替换下的这位老师在专业背景方面有很高的相似度。这个新找来的老师就称为被替换下的老师的工具变量 (Instrumental Variable，简称 IV) 。接下来，让我们一起学习 IV 估计。

如果 “王小二面试” 时找来一个代替老师，那么这位新老师给的面试分数还是有一定的随机性，一个主要的原因是新找来的这位老师可能与被替换的那位老师之间的相关性不够强。为了控制面试得分偏差，我们可以多找几个老师。不妨再找一个老师，这两个老师就称为被替换下来的老师的两个工具变量。

4. 动态面板回归法

基本思想是将解释变量和被解释变量的滞后项作为工具变量（IV）。其实，这种处理方法，除非万不得已，不推荐这种方法，也不太相信这种方法能真正缓解内生性问题。可是，确实很多人都在用。

1.2 因果分析两个框架：Rubin potential Outcome / RCM

快手因果推断与实验设计

potential outcome model （虚拟事实模型 ），也叫做Rubin Causal Model（RCM），希望估计出每个unit或者整体平均意义下的potential outcome，进而得到干预效果treatment effect(eg. ITE/ATE).
所以准确地估计出potential outcome是该框架的关键，由于混杂因子confounder的存在，观察到的数据不用直接用来近似potential outcome，需要有进一步的处理。

核心思想：寻找合适的对照组

1.3 因果分析两个框架： Pearl causal Graph因果图

快手因果推断与实验设计

有向图描述变量之间的因果关系。通过计算因果图中的条件分布，获得变量之间的因果关系。有向图指导我们使用这些条件分布来消除估计偏差，其核心也是估计检验分布、消除其他变量带来的偏差。

1.4 两个框架之间的联系


目的都是为了计算存在混淆变量时，干预变量时对结果的影响，都需要对因果关系作假设，以及控制带来偏差的变量；
不同点在于：
Rubin框架估计的因果效应主要是干预前后的期望差值
而Pearl框架下，我们估计的是干预前后的分布差异
Rubin框架解决的问题是因果效应的估计和统计推断
Pearl框架更偏向于因果关系的识别。

1.5 一些名词概念与解释

通俗解释因果推理 causal inference

  • unit:因果推理中的原子研究对象，可以是实物，也可以是概念，可以是一个或者多个。在一些框架下，不同时刻的同一对象被认为是不同的units。
  • treatment：施加给unit的操作。也叫做干预、介入等。
  • variables:unit自带的一些属性，比如患者的年龄，性别，病史，血压等。在treatment过程中不受影响的variable叫做pre-treatment variables，比如患者的性别在多数情况下是不变的；对应的，收到影响的variable叫做post-treatment variables。多数情况下，variables指的是Pre-treatment variables。一些文献中也叫做context。
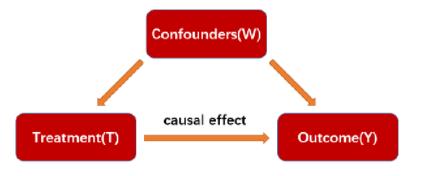
  • Confounders:会影响treatment选择和结果的一些变量。比如同一剂量的药剂在不同年龄的人群的结果可能不一样，或者说不同年龄的药剂选择会不同。有一些文献中也叫做协变量，covariate。
  • potential outcome:施加给对象的操作所能产生的所有可能产生的结果。包含observed outcome和反事实结果。
  • factual outcome:施加给对象的操作最终观测到的结果，记做Y.
  • 倾向分数propensity score：p(x) = P(Wi = 1|Xi = x)，反映出样本x选择treatment的可能性。
  • 选择偏倚selection bias：由于Confounders的存在，treatment组合对照组的分布有可能不一致，因此导致出现偏差，这也使得推理更加困难。
  • pre-treatment variables : 不受干预影响的变量，也叫做背景变量，比如吃药问题的天气
  • post-treatment variables : 受干预影响的变量，比如吃药问题中的食欲

1.9 因果推断与回归的差异？

https://www.zhihu.com/question/266812683/answer/505659271

回归是工具，意味着不管是因果推断还是预测，都可以使用回归;回归在因果推断中，只是拟合条件期望的工具。
Rubin因果只有在非常强的假设前提下才能使用回归（外生性假设，又名CIA假设，又名unconfoundedness假设）

1.0 额外：调节效应与中介效应

中介效应、调节效应是什么？

由这里出发我们再来看另外一对非常有意思的概念：调节效应与中介效应，这俩应该也是可以用因果链来描述的。

中介作用是研究X对Y的影响时，是否会先通过中介变量M，再去影响Y；即是否有X->M->Y这样的关系，如果存在此种关系，则说明具有中介效应。

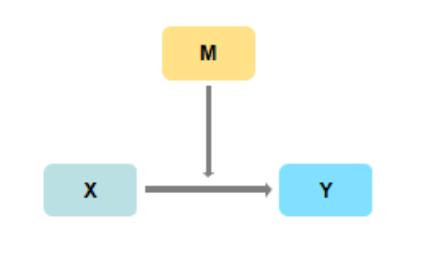
调节作用是研究X对Y的影响时，是否会受到调节变量Z的干扰

2 pearl 因果图的一些定义


我们通常通过因果图来进行用户行为链路的研究。Rubin流派常用来估计变量之间的一度关系，但当我们面对一些未知问题时，我们想了解的是有哪些变量真正影响我们关心的结果变量，以及变量之间的相互影响和用户行为链路是什么，有效过程指标是什么，这些时候我们用到因果图的方法。

在生成因果图中，常遇到的限制是算法层面的，比如我们在优化目标函数的时候，需要遍历所有的因果图，是一个NP-hard问题，我们需要有效的算法得到想要的估计，市面上的算法大概分为两类：

  • Constraint-based Algorithms
  • Score-based Algorithms

因果图的结构是预设的还是模型结构输出的？
A：主要是模型输出的，但是在算法中我们可以限定哪些变量是父节点，哪些是子节点，如果最后结果与假设相悖，会发现假设的父节点下是没有任何子节点的。

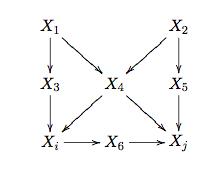
2.1 有向无环图(Directed Acyclic Graph) - DAG

有向图中 “父亲” 和“后代”的概念：有向箭头上游的变量是“父亲”，下游的变量是“后代”。

图模型也并不是 Judea Pearl 发明的。但是，早期将图模型作为因果推断的工具，成果并不深刻，大家也不太清楚仅仅凭一个图，怎么能讲清楚因果关系。教育、心理和社会学中常用的结构方程模型（structural equation model: SEM），就是早期的尝试；甚至可以说 SEM 是因果图的先驱。

2.2 do 算子——在干预的前提下的概率

DAG 中的箭头，似乎表示了某种 “因果关系”。但是，要在 DAG 上引入“因果” 的概念，则需要引进 do 算子，do 的意思可以理解成 “干预” （intervention）。
没有“干预” 的概念，很多时候没有办法谈因果关系。
根据 do 算子，便可以定义因果作用。比如二值的变量 Z Z Z 对于 Y Y Y 的平均因果作用定义为:

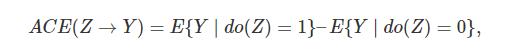
https://www.zhihu.com/question/283897078/answer/756671333
p(y|do(x))实际上就是一个普通的条件分布，但它不是基于 p(x,z,y,…)的，而是pdo(X=x)(x,z,y,…)。这里的pdo(X=x)是我们如果实际进行干预的话会观察到的数据的联合分布。所以p(y|do(x))是从随机对照试验或A/B测试收集到的数据中学习的条件分布，其中x由实验者控制。

2.3 “后门准则”（backdoor criterion）和“前门准则”（frontdoor criterion）

因果推断简介之五：因果图 (Causal Diagram)

如果整个 DAG 的结构已知且所有的变量都可观测，那么我们可以根据上面 do 算子的公式算出任意变量之间的因果作用。但是，在绝大多数的实际问题中，我们既不知道整个 DAG 的结构，也不能将所有的变量观测到。因此，仅仅有上面的公式是不够的。
“后门准则”（backdoor criterion）和“前门准则”（frontdoor criterion）：

这两个准则的意义在于：

  • （1）某些研究中，即使 DAG 中的某些变量不可观测，我们依然可以从观测数据中估计出某些因果作用；
  • （2）这两个准则有助于我们鉴别“混杂变量”和设计观察性研究。

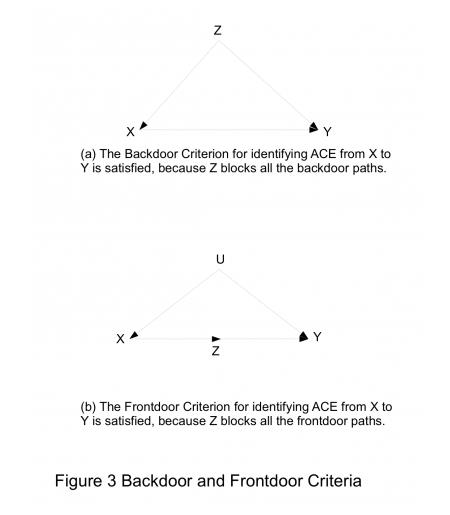
简单来看一下：

  • 后门准则：Z可以同时影响or产生 X/Y，那么Z就相当于X/Y因果关系的后门（不影响X-> Y之间，影响两者），Z也是X/Y的混杂因子
  • 前门准则：Z影响X-> Y的前门路径（直接影响X->Y）

检验得到的结论：

  • 是否有混杂变量在X-> Y之间？
  • 一些变量Z是影响X -> Y的前门路径（Z在X/Y之间，X一定通过Z影响Y），还是后门路径（Z同时影响X/Y）

2.4 后门、前门准则四则例子

再来看四个例子：

根据后门准则， X 阻断了 T 到 Y 的后门路径，因此，根据 X 做调整可以得到 T 对 Y 的因果作用。
如果实际问题符合图（a），那么我们需要用调整后的估计量。

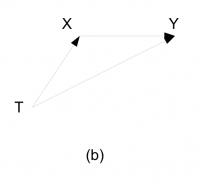
X 是 T 的 “后代” 且是 Y 的“父亲”。很多地方称，此时 X 处于 T 到 Y 的因果路径上（中介效应）。
直观的看，如果忽略 X，那么 T 和 Y 之间的相关性就是 T 对 Y 的因果作用，因为 T 和 Y之间的后门路径被空集阻断，我们无须调整。
如果此时我们用 X 进行调整，那么得到的是 T 到 Y 的“直接作用”。

T 和 Y 之间的相关性就是因果作用。但是，复杂性在于 X 和 Y 之间有一个共同的但是不可观测的原因 U。
此时，不调整的相关性，是一个因果关系的度量。
但是，如果我们用 X 进行调整，那么给定 X 后，T 和 U 相关，T 和 Y 之间的后门路径被打通，我们得到的估计量不再具有因果的含义。
这种现象发生的原因是，(T,U,X)(T,U,X) 之间形成了一个 V 结构：虽然 T 和 U 之间是独立的，但是给定 X 之后，T 和 U 不再独立。

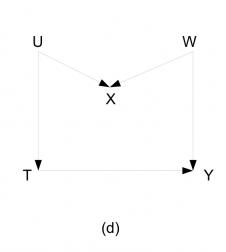
这个图常常被 Judea Pearl 用来批评 Donald Rubin，因为它存在一个有趣的 M 结构。
在这个图中，由于 V 结构的存在，T 和 Y之间的后门路径被空集阻断，因此 T 和 Y 之间的相关性就是因果性。
但是由于 M 结构的存在，当我们用 X 进行调整的时候， U 和 W 之间打开了一条 “通路”（它们不再独立），因此 T 和 Y 之间的后门路径被打通，此时 T 和 Y之间的相关性不再具有因果的含义。

2.5 因果图用DAG来表示的一些问题

  • 复杂系统以及时序的结构中，不一定适用
  • 更为严重的问题是，实际工作中，我们很难得到一个完整的 DAG，用于阐述变量之间的因果关系或者数据生成机制，使得 DAG 的应用受到的巨大的阻碍。

3 Potential Outcome / RCM 中的一些方法

快手因果推断与实验设计
涉及到计量中政策评估【DID, 合成控制, 匹配, RDD四种方法比较, 适用范围和特征】有四种主要的方法：

3.0 随机自然实验

Y1(x)，Y0(x)表示个体i接受治疗的个体因果作用，但是对于单个个体来说，要么接受treatment，要么不接受，Y1(x)，Y0(x)中必然会缺失一个，但在T做随机化的前提下，我们可以识别总体的ATE：

这是因为

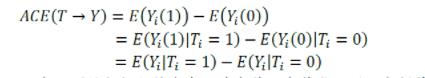
最后一个等式表明ATE可以由观测的数据估计出来。其中第一个等式用到了期望算子的线性性(非线性的算子导出的因果度量很难被识别!);
第二个式子用到了随机化，即 ：

T⊥(Y(1), Y(0))(⊥表示独立性)，
非常重要 ，也就是T 与 Y需要相互独立，无内生性
后面的方法都是围绕他展开

但是实际应用中，随机化实验是最“贵”的因果推断方式，有时候我们无法控制“treatment”，
更多时候成本实在太高，我们只能拨一小波人进行实验，所以这种“黄金标准”并不算实用。

3.1 方法一:双重差分 - difference-in-difference -DID

3.1.1 DID介绍

因果推断综述及基础方法介绍（一）

【3.0章节】 中随机实验有提到，ATE = E(Yi|Ti=1)−E(Yi|Ti=0)的前提是T⊥(Y(1),Y(0))，
也就是干预与Y是独立的、无因果、非内生
那如果不符合这个条件应该怎么办？
有一个比较老且基础的方法是双重差分法，也就是差分两次。

这张图讲得非常清楚，首先为什么我们不能用ATE = E(Yi|Ti=1)−E(Yi|Ti=0)，举个 ，我们给一些人发权益，另一些人不发，我们怎么能知道权益带来的购买效果是怎么样的呢？简单的方法就是给发权益的人购买数加和，不发权益的人购买数加和，然后两个加和相减就好啦，但是如果这两部分人本来不发权益的时候购买数就不一样呢？

那就减两次，从上图来说，我们把这两群人发权益之前t0的购买数相减，得到一个差值，相当于这两群人的固有差距，再把这两群人发权益之后t1的购买数相减，相当于这两群人被权益影响之后的差距，后面的差距减去前面的差距，就会得到权益对于差距有多少提升（降低），以此作为权益的effect。

这个方法的问题在于有个比较强的要求是，趋势平行，也就是要求t0到t1之间，两群人的购买概率变化趋势是一样的（图中那个平行线），这其实是一个很强的假设，所以这个方法我个人来讲不算非常认可。

3.1.2 快手中的DID模型

同一对象的同一干预treatment，前、后两个时间段的差异,
关键假设是，政策干扰前存在平行趋势，且实验干扰效应不随时间变化。
双重差分可以用来消除那些对后期可能存在干扰因素，得到实验效果估计。


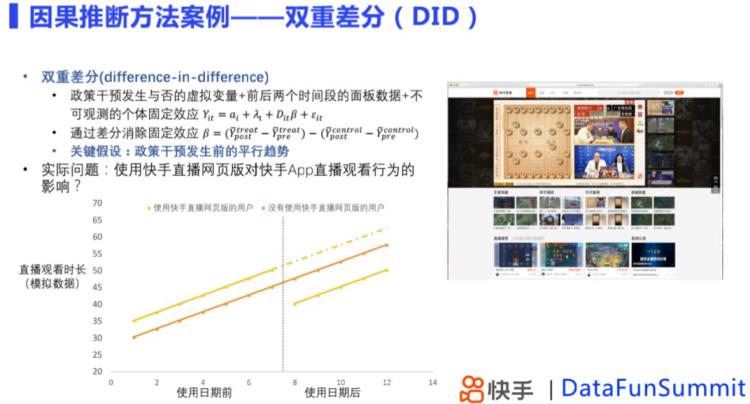
快手的升级方案：分不同类型进行分项评估
用户的行为会发生变化，且不同用户的行为是不一致的，当不同表现用户都在实验组，传统的DID模型估计实验效应会产生偏差。
按照用户的状态是否更改分为不同类型，对不同类型用户分别做DID估计，再进行加权平均，得到修正后DID实验效果值。

3.2 方法二：合成控制SCM——Synthetic Control Method

当treatment施加到一个群体或者地区上时，很难找到单一的对照组，这种时候采用合成控制方法构造虚拟对照组进行比较，原理是构造一个虚拟的对照组，通过treatment前的数据上学习的权重，拟合实验组在实验开始前的数据，模拟实验组用户在没有接受实验情况下的结果，构造合成控制组，实验开始后，评估实验组和合成控制组之间的差异。

参考：合成控制法什么鬼? 因果推断的前沿方法指南

听到最多的例子是，加州于1989年实施的禁烟法案， 但愿看看该法案是否下降了烟草的消费量。由于这个禁烟法案只在加州范围内有政策效果，所以传统的DID方法就没有那么好用了，由于这里的实验组就只有一个成员——加州。ui
对于这种问题，咱们迫切想要获得因果关系，所以合成控制法就出现了而且获得快速推广。

SCM的基本思想是，使用其余38个未实施禁烟法案的州的加权平均来合成一个“加州”，经过对比真实的加州和合成的加州在1989年禁烟法案以后香烟消费量的差别来识别出政策效应。code

在合成控制法中，有一些关键变量比较重要，所以值得咱们提出来单独说一说。如下就是咱们使用一个吸烟数据集，就加州1989年实施的禁烟法案对该州香烟消费量(销售量)的影响所作的合成控制法

合成的一种方法是利用，其他38个洲，1970-1988数据构造回归，
然后进行预测，预测接下来1988-2000的情况与实际的情况进行对比

3.3 断点回归模型

该模型的主要思想在于，寻找一个参考变量，该变量的某临界值能够决定哪个个体能够成为政策干预对象即处理组，哪个个体不能成为政策干预对象即控制组，将控制组的结果变量作为处理组的反事实状态。

断点回归可分为精确断点回归和模糊断点回归。

精确断点回归假设干预分配完全由参考变量决定，而模糊断点回归则假设干预状态不是完全由参考变量决定，还与其他未观测到的因素有关。

精确断点回归与其他几种政策评估的不同之处在于，其不满足共同区间假设，即当参考变量大于临界值时，所有个体都进入处理组，而当参考变量小于临界值时，所有个体都进入控制组。

断点回归模型的主要缺点在于，若个体能够精确控制是否接受政策的参考变量，那么临界点附近的干预状态的分配就接近完全随机实验的结果，断点回归的估计将无效。

此外，断点回归模型和完全随机实验一样，内部有效性较强，而外部有效性较弱，即只能估计断点处的平均因果效应，不能简单推广到其他位置。

针对该问题，Angrist 和Rokkanen（2015）引入了类似于匹配方法的条件独立性假设，假设引入其他协变量后，参考变量和潜在结果之间是独立的，只要根据协变量而不是参考变量进行匹配，可以将因果效应外推到断点左右任意位置。

3.4 Rubin Causal Model(RCM)与倾向性得分

3.4.0 从matching -> 倾向性得分

随机化试验那部分我们讲到了：

T⊥(Y(1), Y(0))(⊥表示独立性)

这个公式其实包含了较强的可忽略性（Ignorability）假定，但我们之前说了，这种方式比较“贵”，所以通常我们会希望收集足够多的X，使得：

3.4.1 基于倾向性评分法的因果推断

倾向性评分法由Rosenbaum和Rubin于1983年首次提出，是控制混淆变量的常用方法，其基本原理是将多个混淆变量的影响用一个综合的倾向性评分来表示，从而降低了混淆变量的维度。

倾向性评分是给定混淆变量W的条件下，个体接受Treatment的概率估计，即 P(T=1|W)。
需要以Treatment为因变量，混淆变量Confounders为自变量，建立回归模型(如Logistic回归)来估计每个研究对象接受Treatment的可能性。

回归：T~W

3.4.2 因果效应估计三种方法

需要择一选择：

  • 倾向性评分匹配法(Propensity Score Matching，PSM)
    PSM将处理组和对照组中倾向性评分接近的样本进行匹配后得到匹配群体，再在匹配群体中计算因果效应。最常用的匹配方法是最近邻匹配法(nearest neighbor matching)，对于每一个处理组的样本，从对照组选取与其倾向评分最接近的所有样本，并从中随机抽取一个或多个作为匹配对象，未匹配上的样本则舍去。
  • 倾向性评分分层法(Propensity Score Stratification，PSS)
    PSS将所有样本按照倾向性评分大小分为若干层(通常分为5-10层)，此时层内组间混淆变量的分布可以认为是均衡的，当层内有足够样本量时，可以直接对单个层进行分析，也可以对各层效应进行加权平均。当两组的倾向性评分分布偏离较大时，可能有的层中只有对照组个体，而有的层只有试验组的个体，这些层不参与评估因果效应。PSS的关键问题是分层数和权重的设定。可通过比较层内组间倾向性评分的均衡性来检验所选定的层数是否合理，权重一般由各层样本占总样本量的比例来确定。
  • 倾向性评分加权法(Propensity Score Weighting，PSW)
    PSW在计算得出倾向性评分的基础上，通过倾向性评分值赋予每个样本一个相应的权重进行加权，使得处理组和对照组中倾向性评分分布一致，从而达到消除混淆变量影响的目的。

3.4.3 倾向性评分法的均衡性检验

倾向性评分法要求匹配后样本的所有混淆变量在处理组和对照组达到均衡，否则后续分析会有偏差，因此需要对匹配之后的样本进行均衡性检验。

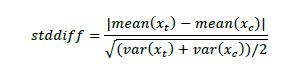
3.4.4 反驳

反驳(Refute)使用不同的数据干预方式进行检验，以验证倾向性评分法得出的因果效应的有效性。反驳的基本原理是，对原数据进行某种干预之后，对新的数据重新进行因果效应的估计。
理论上，如果处理变量(Treatment)和结果变量(Outcome)之间确实存在因果效应，那么这种因果关系是不会随着环境或者数据的变化而变化的，即新的因果效应估计值与原估计值相差不大。
反驳中进行数据干预的方式有：

  • 安慰剂数据法：用安慰剂数据(Placebo)代替真实的处理变量，其中Placebo为随机生成的变量或者对原处理变量进行不放回随机抽样产生的变量。
  • 添加随机混淆变量法：增加一个随机生成的混淆变量。
  • 子集数据法：随机删除一部分数据，新的数据为原数据的一个随机子集。

3.4.5 倾向性得分案例

Lalonde数据集是因果推断领域的经典数据集
数据集共包含445个观测对象，一个典型的因果推断案例是研究个人是否参加就业培训对1978年实际收入的影响。
treatment变量，就业培训与否0/1
混淆变量为age、educ、black、hisp、married、nodeg。

3.4.5.1 第一步:使用倾向性评分法估计因果效应

各种倾向性评分法的因果效应估计值在图表7中，由于不同方法的原理不同，估计的因果效应值也不同。其中倾向性评分匹配法(PSM)因果效应估计值为2196.61，即参加职业培训可以使得一个人的收入增加约2196.61美元
我们计算ATE(Average Treatment Effect)，即在不考虑任何混淆变量的情况下，参加职业培训(treat=1)和不参加职业培训(treat=0)两个群体收入(re78)的平均差异，在不考虑混淆变量下，参加职业培训可以使得一个人的收入增加约1794.34美元。

另外从ATE和几个估计方法的差异来看，ATE 与PSS/PSW差异不大（说明混淆变量影响不大），PSM差异较大，所以可能PSM不太稳定。

3.4.5.2 第二步：评估各倾向性评分方法的均衡性

图表8展示了各倾向性评分方法中，每个混淆变量的标准化差值stddiff。总体来看，倾向性评分加权法(PSW)中各混淆变量的标准化差值最小(除了hisp)，说明PSW中混淆变量在处理组和对照组间较均衡，其因果效应估计值可能更可靠。

3.4.5.3 第三步：反驳

图表8展示了100次反驳测试中，三种倾向性评分法的每类反驳测试结果的均值。我们将三种倾向性评分法在真实数据下的因果效应估计值放在图表9最右侧进行对比。
在安慰剂数据法中，由于生成的安慰剂数据(Placebo)替代了真实的处理变量，每个个体接收培训的事实已不存在，因此反驳测试中的因果估计效应大幅下降，接近0，这反过来说明了处理变量对结果变量具有一定因果效应。
在添加随机混淆变量法和子集数据法中，反驳测试结果的均值在1585.19~1681.75之间。

对比真实数据的因果估计效应值，PSM的反驳测试结果大符下降，说明其估计的因果效应不太可靠；
PSW的反驳测试结果与真实数据因果效应估计值最接近，说明其因果效应估计值可能更可靠。


所以，可以需要得到的结论：

  • 需要挑选PSM/PSS/PSW中一个合适的方法
  • 然后来看因果是正向还是负向（因果效应估计值的正负）

3.5 DID / PSM / DID(PS)M的差异？

DID, PSM 及 DID+PSM 有何差异？DID 要假定不可观测效应随时间变化趋势相同？

  • DID: difference in difference, 双重差分；
  • PSM: propensity score matching, 倾向评分匹配；
  • DID(PS)M: difference in difference (propensity score) matching, 双重差分（倾向评分）匹配

一个比较简单的差异对比版本：

  • DID是比较四个点，Treated before, treated after; control before, control after。
  • Matching是比较两个点：Treated, control
  • DID＋Matching是用matching的方法来确定treated和control。

3.6 元学习 —— Uplift Model

智能营销增益（Uplift Modeling）模型——模型介绍（一）

5 因果推断与机器学习

快手因果推断与实验设计

5.1 因果推断与机器学习的异同


因果分析的语言，核心在于因果关系的识别，即合理的估计处理前和处理后现有条件期望的差异，也可以是一种处理缺失数据的问题，在因果推断上我们非常关心的是如何准确的估计结果以及结果的方差。而在机器学习中，我们使用准确度来衡量机器学习模型的好坏，其目标是在训练集上估计一个条件期望，使得测试集上MSE最小。机器学习可以通过cross-validation（模型参数）的方法去数据驱动的选择一个最佳模型形式，与传统计量经济学方法相比不需要复杂的假设，例如function form的假设，从这种意义上机器学习能够更准确的预测。
但是在因果推断问题上，机器学习的局限性在于，无论用什么机器学习方法，因果识别的条件都不能被放松；同时在机器学习模型通常使用的正则化和过拟合处理，会带来有偏估计，因此我们需要消除这种估计的偏差；
在统计推断上，机器学习的局限性在于，有些模型不能直接计算方差，并且有时即使可以计算，方差的收敛速度也未必能够达到预期，所以针对这些问题，下面介绍了几种方法。

5.2 方法一：双重机器学习

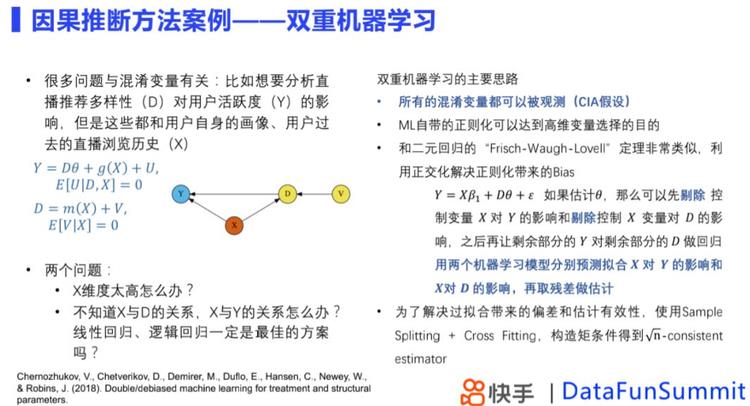
因果推断会遇到混淆变量的问题，比如想要去分析直播推荐多样性对用户活跃度的影响，但是这些都和用户历史相关。传统计量经济学方法可以解决这个问题，但是依赖很多强假设，强假设下，得到的估计不一定合理，双重机器学习为这个问题提供了解决的思路。

双重机器学习假设所有混淆变量都可以被观测，其正则化过程能够达到高维变量选择的目的，与Frisch-Waugh-Lovell定理相似，模型通过正交化解决正则化带来的偏差。
除了上面所描述的，还有一些问题待解决，比如在ML模型下存在偏差和估计有效性的问题，这个时候可以通过Sample Splitting 和 Cross Fitting的方式来解决，具体做法是我们把数据分成一个训练集和估计集，在训练集上我们分别使用机器学习来拟合影响，在估计集上我们根据拟合得到的函数来做残差的估计，通过这种方法，可以对偏差进行修正。在偏差修正的基础上，我们可以对整个估计方法去构造一个moment condition，得到置信区间的推断，从而得到一个有良好统计的估计。

5.3 方法二:因果随机森林模型

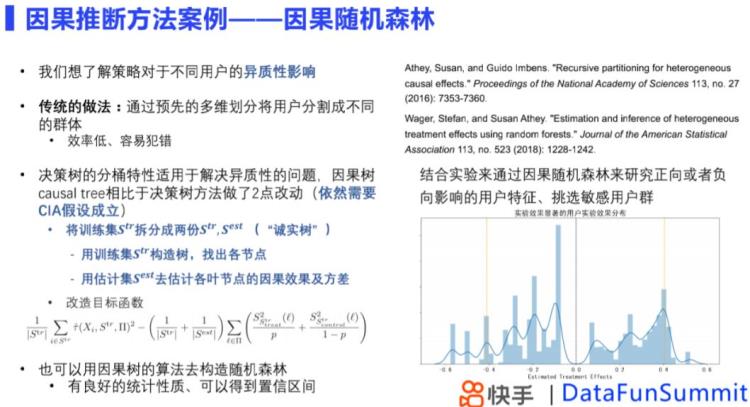
我们通常探究策略对于不同用户异质性的影响，即哪些用户更容易被影响以及影响有多大，传统做法是多维分析，但是效率低，容易犯错。这时可以结合机器学习的方法，这里选择了决策树方法，因为决策树的分桶特性能够帮助解决异质性问题，相对于传统方法因果树做了两点改动:

把数据分成训练集和估计集，一部分训练集去构造树，另一部分估计集去估计因果效应和方差；
在树的分区方式上，使用各个节点的方差对目标函数加以修正。
通常情况下，我们结合实验来做分析。比如在实验中，通过因果树得到因果效应的分布，然后挑选出来那些实验效果显著的用户，去分析他们的特征，以及找到敏感用户，帮助我们了解策略的影响，作出下一步迭代。

5.4 方法三:Meta-Learner for Uplift Modeling


Uplift-modeling是另一种定位敏感人群的方法，和因果树的步骤有差别。核心是利用实验数据对实验结果变量建模，利用得到的模型估计条件平均处理效果。Uplift-modeling具有不同的学习方式，主要有S-Learner 、T-Learner和X-learner。和因果树相比，Meta-Learner是一种间接建模方式，实现快但一些场景下误差较大。

CIA假设往往不能满足，应该如何降低影响？
A：现在很多的包括双重机器学习等方法都有很多的扩展，比如当有些合适的工具变量会有些合适的拓展的工具方法，另外可以通过一些matching的方法去构造些满足条件的样本，但是这个东西也不是完全精确，很多时候需要靠人为的逻辑判断。

6 快手的因果推断与实验设计

快手因果推断与实验设计

6.1 快手：双边实验设计


在双边实验中，同时进行了主播侧和观众侧的分流，主播侧一部分是上了挂件，观众侧一部分能看到一部分看不到，双边实验的优点是可以同时检测两端的效果，同时可以帮助检测到组间的转移和溢出。在了解到组间溢出和干扰下，通过双边实验我们可以更加准确的测算处理效应，在挂件场景下，我们认为N3是代表完全没有处理过的效果，Y代表处理后的结果，N3和Y进行差分，计算产品功能推全后的影响，而且，双边实验能够更好的帮助我们归因。

然而双边实验只能描述简单的组间溢出，在个体和个体之间存在干扰的复杂情况下，双边实验是无法帮助我们判断实验效果，例如直播PK暴击时刻这种情况下，我们通过时间片轮转实验解决，即在一定实验对象上进行实验组策略和对照组策略的反复切换。

6.2 快手：时间片轮转实验


时间片轮转的核心在于：

  • 时间片的选择

  • 实验总周期选择

  • 随机切换时间点是什么样子的
    当时间粒度约粗糙，时间上的干扰造成的偏差会越小，但是方差会越大，影响实验的检验效果，针对这个问题，采取的方案是最优设计。

    最优设计的核心假设是：

  • Outcome有一个绝对上界

  • 用户无法知晓下一个时间是否是实验组

  • 如果时间片之间存在干扰，干扰的影响是固定且有限的

当我们不知道一个时间片实验时间节点如何设计时，通常采取的步骤是，预估一个时间，通过实验确定carry over的阶数下限是多少，根据阶数下限，找到最优切换时间点，再进行一次实验，通过实验组和对照组的选择来进行因果效应的估计。其缺点在于，实验周期长，没有办法观测到HTE (heterogeneous treatment estimation)。

6.3 快手：城市实验 + 合成控制


当treatment施加到一个群体或者地区上时，很难找到单一的对照组，这种时候采用合成控制方法构造虚拟对照组进行比较，原理是构造一个虚拟的对照组，通过treatment前的数据上学习的权重，拟合实验组在实验开始前的数据，模拟实验组用户在没有接受实验情况下的结果，构造合成控制组，实验开始后，评估实验组和合成控制组之间的差异。

如何评价微软（Microsoft）推出的 Python 因果推理库 DoWhy？

因果推断简介之五：因果图 (Causal Diagram)
快手因果推断与实验设计

以上是关于因果推断笔记—— 相关理论：Rubin PotentialPearl倾向性得分与机器学习异同的主要内容，如果未能解决你的问题，请参考以下文章

因果推断笔记——自整理因果推断理论解读

因果推断笔记——自整理因果推断理论解读

因果推断笔记——工具变量内生性以及DeepIV

因果推断中期学习小结

因果推断中期学习小结

因果推断笔记——python 倾向性匹配PSM实现示例