什么是并查集?建议收藏
Posted 飞人01_01
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了什么是并查集?建议收藏相关的知识,希望对你有一定的参考价值。

本期文章源码: GitHub
一文彻底搞懂《并查集》!
概念
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题(即所谓的并、查)。比如说,我们可以用并查集来判断一个森林中有几棵树、某个节点是否属于某棵树等。
具体的用法,我们会以下一篇文章《图的相关算法》中,有一个克鲁斯卡尔算法,用于生成最小生成树,会用到并查集。
并查集的主要作用是求连通分支数(如果一个图中所有点都存在可达关系(直接或间接相连),则此图的连通分支数为1;如果此图有两大子图各自全部可达,则此图的连通分支数为2……)
在现实生活中,也是存在着并查集的一些概念,例如最近《天龙八部》里的人物关系,可能你并不认识丐帮的一些小人物,但是你一定认识丐帮帮主乔峰。当你看见一个叫花子,你就会想到他的老大就是帮主乔峰,像这样的场景,就有了一定的归属感, 会自动的认为叫花子就是跟丐帮合并在一起的……

说简单一点,并查集就是将一些数据进行分类,这样数据为一组,那些数据为另一组。如何判断其中两个数据,在不在一个组?我们就会去找每个组的代表,看这两个数据的代表是不是同一个?如果是,那就是在一个组;如果不是,那就不在一个组。所以并查集的大致框架就是下面这样:
//并查集大致框架---代码中的数据(Node),可以是其他,比如二叉树节点、图的边、节点等等 抽象的数据
public class UnionSet {
private HashMap<Node, Node> fatherMap; //key表示当前这个数据,value表示这个数据的代表(父亲)是谁
private HashMap<Node, Integer> sizeMap; //表示当前这个组(集合)的大小
public UnionSet() { //构造方法
fatherMap = new HashMap<>();
sizeMap = new HashMap<>();
}
public void makeSet(List<Node> list) { //生成初始化状态的并查集,刚开始每个数据都是独立的
}
public boolean isSameSet(Node node1, Node node2) { //判断当前这两个数据,是不是一个组的?
}
private Node findFather(Node node) { //查找这个数据,它那个组的代表(父亲)是谁?
}
public void union(Node node1, Node node2) { //将这两个数据,放到一个组
}
}
上面就是大致的框架,就是几个方法:初始化并查集、判断是不是一个组、查找代表、合并到一个组。四个方法,就是并查集。简不简单?
并查集在判断两个数据,是否在一个组时,时间复杂度能做到O(1),所以这种数据结构还是非常有用的。
实现
初始化并查集
我们首先从第一个方法:初始化并查集开始。
传入进去的参数不一定是List,也可以是Collection等等,表示一组数据即可! 首先我们的成员变量只有两个,分别是存储节点的代表 和 当前这个组的大小。初始化时,我们分别认为 每个节点是自己一个人一组的,也就是说,自己一个组,代表就是自己本身;大小的话,就是自己本身咯,也就是1。
//初始化并查集
public void makeSet(List<Node> list) {
if (list == null) {
return;
}
fatherMap.clear();
sizeMap.clear(); //先将表清空
//遍历list,把每一个节点,都放入哈希表中
for (Node node : list) {
fatherMap.put(node, node); //第一个参数是节点本身,第二个参数就是这个组的代表
sizeMap.put(node, 1); //第一个参数是这个组的代表,第二个参数是大小
}
}

判断是不是同一个组
isSameSet 比较简单,就是判断两个数据所在的组的代表,是不是用一个数据即可!如果代表是同一个人,那就是在一个组,反之就不是!
//判断是不是同一个组
public boolean isSameSet(Node node1, Node node2) {
if (node1 == null || node2 == null) {
return false;
}
return findFather(node1) == findFather(node2); //查找各自的代表节点,看是不是同一个。
}
查找当前节点的代表节点
findFather,我自己觉得算是并查集的核心,也这是这个方法,是并查集的查找的时间复杂度能在O(1)的主要因素。
思路就跟二叉树向上查找根结点的思路一样,也就是说,在fatherMap中一直查找,直到一个节点的代表节点(父节点)是它自己本身时,此时就查找完了;然后最关键的一步,就是路径压缩,在我们向上查找的过程中,我们需要记录沿途的所有节点,在查找结束后,我们将沿途的这些节点,在fatherMap中的进行修改,直接将这些节点的代表节点,写成这个组的代表节点,可能听糊涂了,看下图:
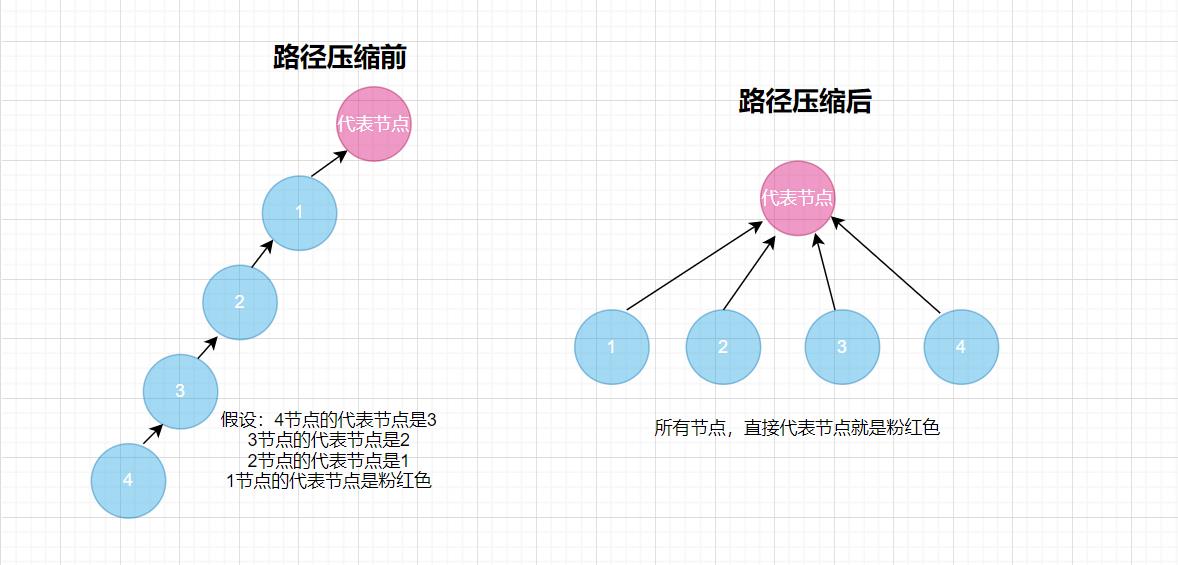
这样的设计,就能使查找的时间复杂度控制在O(1)。
//查找代表节点,并做路径压缩
private Node findFather(Node node) {
if (node == null) {
return null;
}
//查找代表节点
Stack<Node> path = new Stack<>(); //存储沿途的节点
while (node != fatherMap.get(node)) { //代表节点不是自己本身,就继续查找
path.push(node);
node = fatherMap.get(node);
}
//路径压缩
while (!path.isEmpty()) {
Node tmp = path.pop();
fatherMap.put(tmp, node); //此时的node,就是这个组的代表节点
}
return node;
}
合并操作
终于来到了最后的操作:合并。合并也比较简单,记住一个要点:小组挂在大组的下面。也就是说,这一个节点所在的组要小一点,我们直接将他“挂”在另一个组的下面。说简单一点:这一个组的代表节点的vaule域,直接指向另一个组的代表节点。
//合并操作
public void union(Node node1, Node node2) {
if (node1 == null || node2 == null) {
return;
}
int node1Size = sizeMap.get(node1);
int node2Size = sizeMap.get(node2); //分别得到两个节点所在组的大小
Node node1Father = fatherMap.get(node1);
Node node2Father = fatherMap.get(node2); //分别拿到两个节点的代表节点
if (node1Father != node2Father) { //两个节点,不在同一个组,就合并
if (node1Size < node2Size) { //node1 挂在 node2
fatherMap.put(node1Father, node2Father);
sizeMap.put(node2Father, node1Size + node2Size); //新的组,大小是原来两个组的和
sizeMap.remove(node1Father); //小组的数据,就不需要了,删除
} else { //node2 挂在 node1
//跟上面操作类似
fatherMap.put(node2Father, node1Father);
sizeMap.put(node1Father, node1Size + node2Size);
sizeMap.remove(node1Father);
}
}
}
上面就是并查集的所有操作了,是不是很简单呢?
好啦,本期更新到此就结束啦,同学们,下期见!!!
以上是关于什么是并查集?建议收藏的主要内容,如果未能解决你的问题,请参考以下文章