并查集

Posted 2020-10-14

什么是并查集

在计算机科学中，并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。

有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

Union：将两个子集合并成同一个集合。

由于支持这两种操作，一个不相交集也常被称为联合-查找数据结构（union-find data structure）或合并-查找集合（merge-find set）。

其他的重要方法，MakeSet，用于建立单元素集合。有了这些方法，许多经典的划分问题可以被解决。

为了更加精确的定义这些方法，需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素，称为代表，以表示整个集合。

接着，Find(x) 返回 x 所属集合的代表，而 Union 使用两个集合的代表作为参数。

————来自维基百科

算法的思路

使用树来表示每一个集合，因为树上每一个元素都有相同的根。这样，就根就可以用来命名所在的集合
我们可以将树存储在数组中，数组每个成员s[i]表示元素i的父亲，如果i是根，那么s[i]=-1；

算法的基本操作

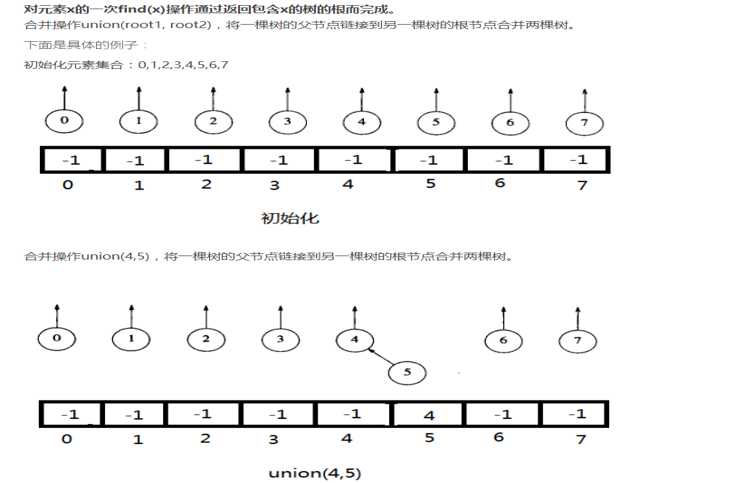
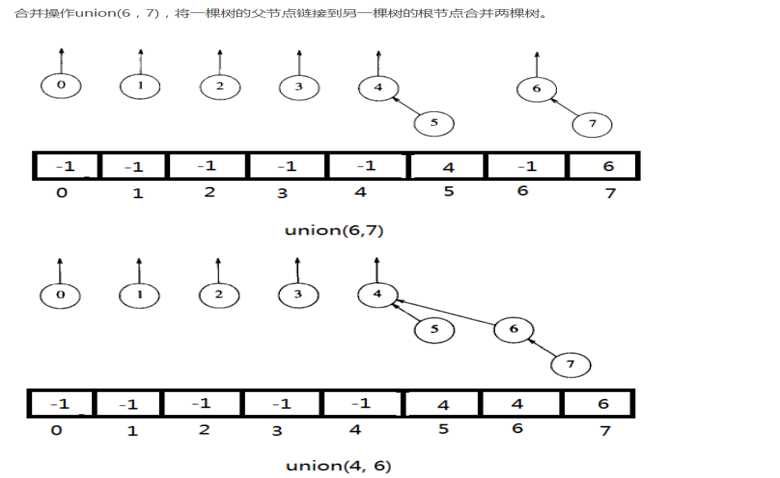
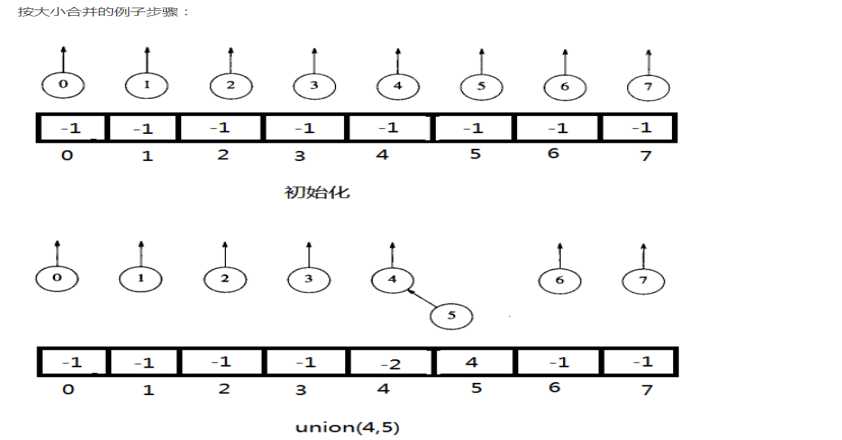
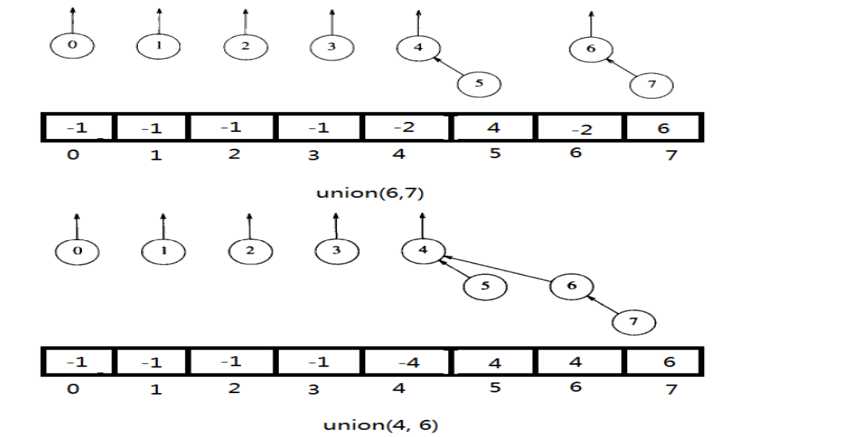
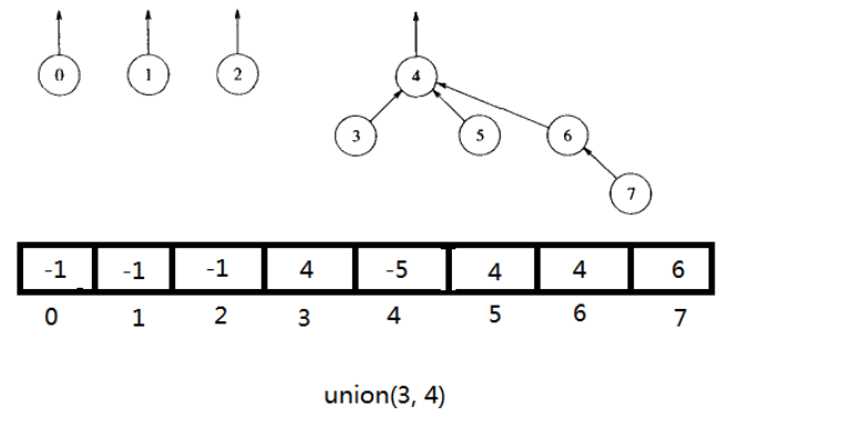
按树大小Union

每个根元素包含它的树的大小的负值。合并的时候首先检查树的大小，将较小的树成为较大树的子树
新的树的大小为两棵树大小的和。

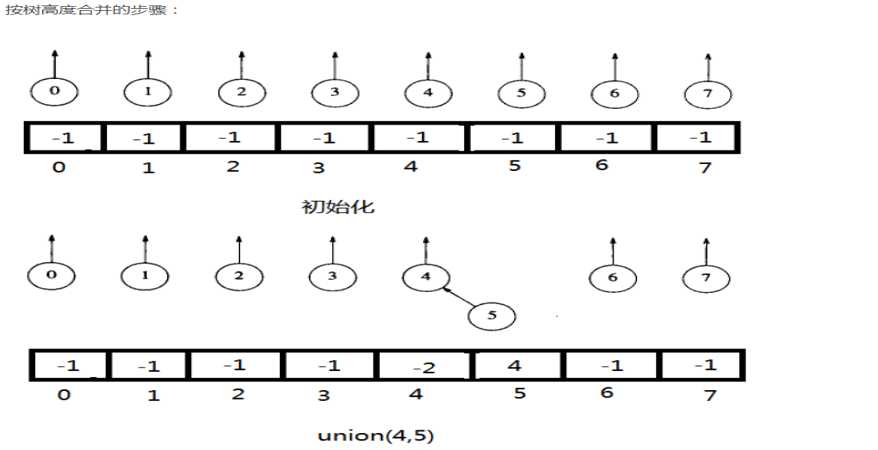
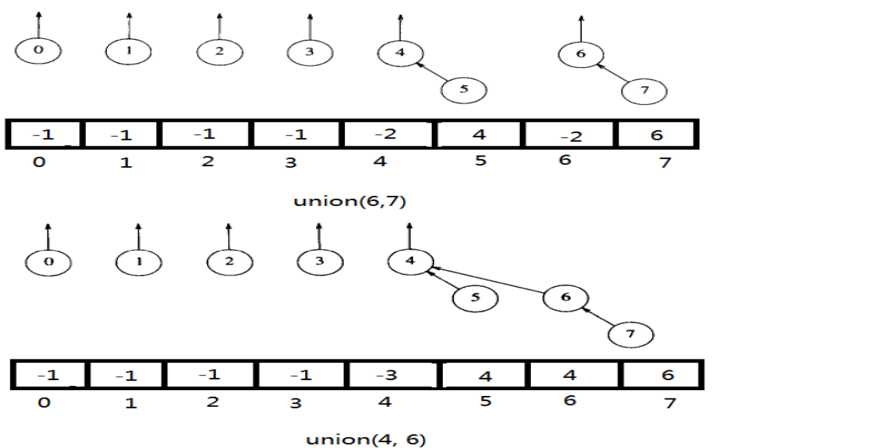
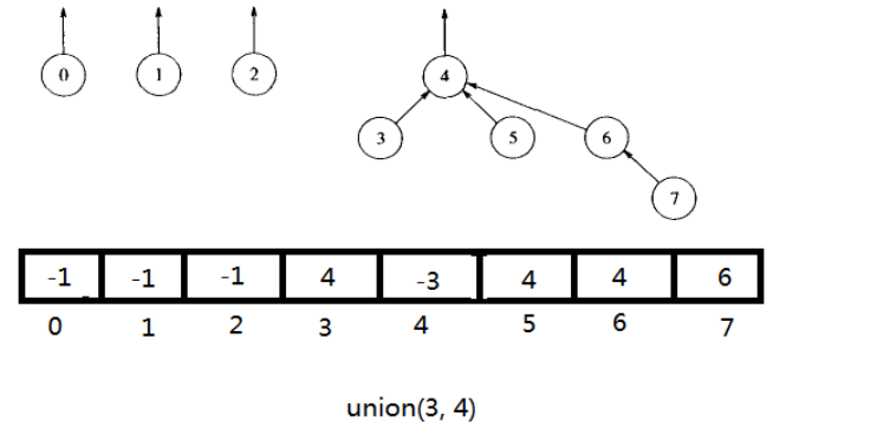
按树深度Union

每个根元素包含它的树的高度的负值。只有合并的两棵树高度相等的时候才需要更新树的高度(根元素的值减去1）

算法代码实现

Find

int Find(int x)
{
    if (s[x] < 0)
        return x;
    else
        return s[x] = Find(s[x]);//路径压缩
}

Union By Size

void UnionBySize(int root1, int root2)
{
    if (s[root1] > s[root2])//root2树比较大
    {
        s[root2] += s[root1];//更新树的大小
        s[root1] = root2;
    }
    else
    {
        s[root1] += s[root2];
        s[root2] = s[root1];
    }
}

Union By Height

void UniontByHeight(int root1, int root2)
{
    if (s[root2] < s[root1])//root2树比较深 直接合并
        s[root1] = root2;//root1成为root2的子树
    else
    {
        if (s[root1] == s[root2])//如果两树深度相等
            s[root1]--;
        s[root2] = root1;
    }
}