算法笔记：查找算法

Posted 2021-09-12 变身独角兽

二分查找

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列

适用场景

1.必须采用顺序存储结构。
2.必须按关键字大小有序排列。

原理与步骤

对于给定的已经有序的数列，我们需要在该数列中查找是否存在某个元素。

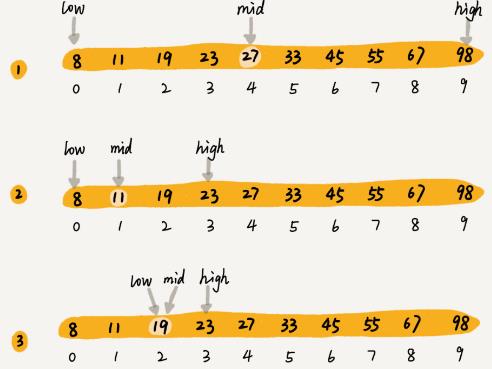
每次都与数列最中间的元素进行比较，可以缩小一半的查找区间，直至找到目标元素或者区间被缩小为0，元素不存在。比如下面的数列中，我们想要查找元素19，那么大致的过程就是这样的：

复杂度

• 时间复杂度
  二分查找法基本思想是将n个元素分成大致相等的两部分，取a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.
  时间复杂度即是while循环的次数。
  n个元素的每次循环折半，n,n/2,n/4,…n/2^k（k就是循环的次数）
  最差情况下，执行最后一次折半，所得数列长度为1，即n/2^k=1，由此可得k=log2n,（是以2为底，n的对数）
  由上所述，时间复杂度为：O(h)=O(log2n)
• 空间复杂度

实例

• 题目
  给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
  说明：
  你可以假设 nums 中的所有元素是不重复的。
  n 将在 [1, 10000]之间。
  nums 的每个元素都将在 [-9999, 9999]之间。
• 代码

int search(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize - 1;
    int mid, temp;
    while (left <= right)  //不一定能查找到，遍历完
    {
        mid = left + (right - left)/2;
        temp = nums[mid];
        if (temp == target)
            return mid;
        else if (temp < target)
            left = mid + 1;
        else
            right = mid - 1;
    }
    return -1;

}