学习数据结构笔记 ---查找算法(线性查找,二分查找,插值查找,斐波那契查找)
Posted 小智RE0
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了学习数据结构笔记 ---查找算法(线性查找,二分查找,插值查找,斐波那契查找)相关的知识,希望对你有一定的参考价值。
B站学习传送门–>尚硅谷Java数据结构与java算法(Java数据结构与算法)
1.顺序/线性查找算法(Sequential Search)
线性查找的话,比较简单,直接遍历数组,找到对应的数值即可
顺序查找/线性查找 ; 作为最基本的查找算法;查找过程为:从第一个元素或最后一个开始,逐个进行比较要查找的数值;若找到就返回下标;
如果说一直找都没找到,那么就停止查找,并返回一个约定好的固定结果,表示没有找到;
/**
* @author by CSDN@小智RE0
* 线性查找
*/
public class LinearSearchTest02 {
//测试;
public static void main(String[] args) {
//需要查找元素的数组;
int[] array = {20,15,23,2,1,8,45};
//需要查找的元素;
int num = 23;
//测试执行
int i = LinearSearch(array, num);
if(i==-1){
System.out.println("未找到指定元素");
}else {
System.out.println("指定元素已找到,下标为->"+i);
}
}
//线性查找;
public static int LinearSearch(int[] array,int key){
//直接遍历数组,找到关键值后,就返回这个数组的下标;
for (int i = 0; i < array.length; i++) {
if(array[i] == key){
return i;
}
}
return -1;
}
}
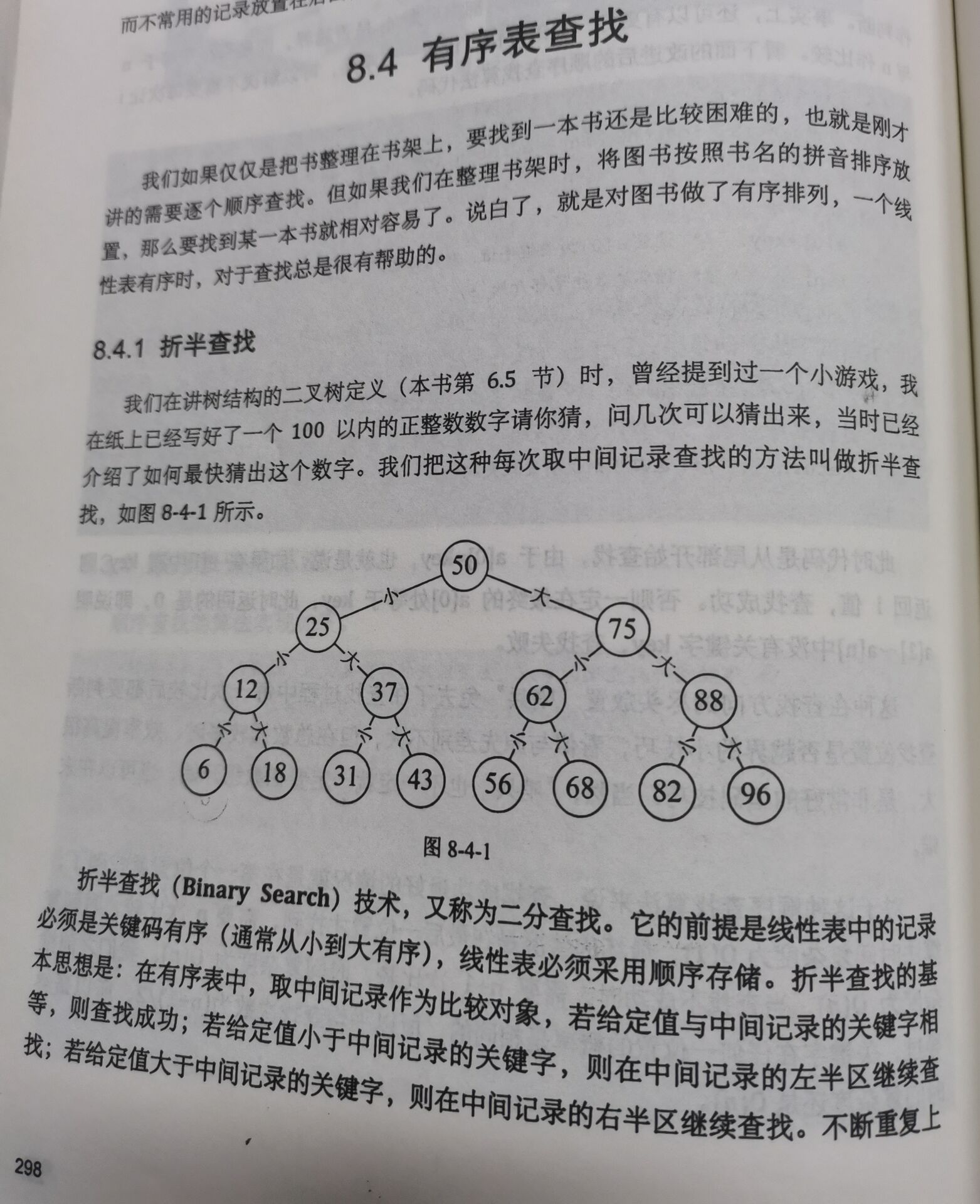
2.二分查找算法
实际上,可以联想到之前的二叉搜索树
<<大话数据结构>>⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇⬇
注意首先要保证二分搜索前的这个数组是有序的;
实际上,正如其名,就是首先要找到这个要查找的数组的中心点元素;
然后再根据比较要查找的数和中间数进行比较;
- 如果这个要查找的值,比中心值还小,就得在中心点的左边去查找;(递归)
- 如果这个要查找的值,比中心值还大,就得在中心点的右边去查找;(递归)
- 若等于中心点了,直接返回这个中心点即可;
- 注意,要还是找不到就得结束;返回一个固定值或者抛出异常.
查找到一个出现位置实现
import java.util.Arrays;
/**
* @author by CSDN@小智RE0
* 二分查找
*/
public class BinarySearchTest {
//测试;
public static void main(String[] args) {
//需要查询的数组;
int[] array = {21,3,0,54,21,67,21};
//要找的关键字;
int num = 21;
System.out.println(" 原数组->"+ Arrays.toString(array));
//需要保证数组是有序的;
Arrays.sort(array);
System.out.println("排序后的数组->"+Arrays.toString(array));
try {
int i = BinarySearchIndexOf(array, 0, array.length, num);
System.out.println("该指定元素在数组中出现位置->"+i);
} catch (Exception e) {
e.printStackTrace();
}
}
/**
* 查找指定元素在已排序的数组中(由小到大排序)出现的位置;
*
* @param array 需要查找的数组
* @param left 左指针索引;
* @param right 右指针索引
* @param key 要查找的关键字
* @return 返回指定元素首次出现的位置;
*/
public static int BinarySearchIndexOf(int[] array, int left, int right, int key) {
if (left > right) {
throw new RuntimeException("未找到指定的元素");
}
//定义中轴点;
int middle = (left + right) / 2;
//中心点的值;
int middleVal = array[middle];
if(middleVal > key){
//向左递归查找;
return BinarySearchIndexOf(array,left,middle - 1,key);
}
else if(middleVal < key){
//向右递归查找;
return BinarySearchIndexOf(array, middle+1, right, key);
}else {
return middle;
}
}
}
注意这种实现方式的话,只能找到其中一个数值;
但是我这里有3个21;
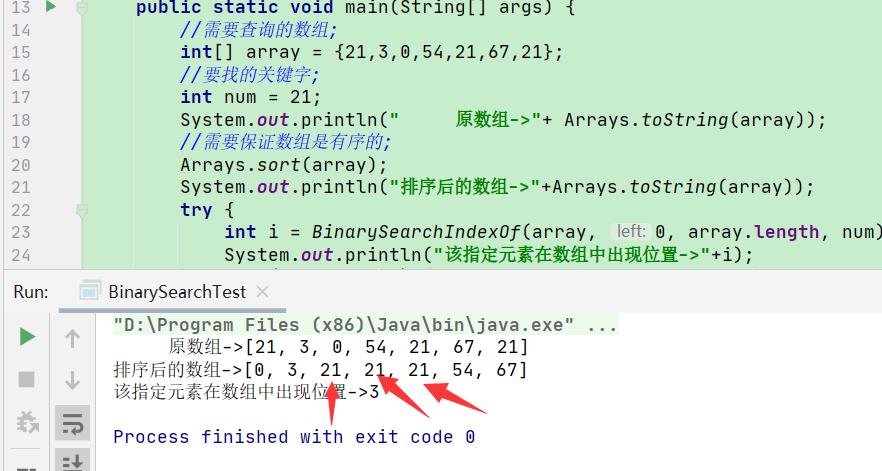
那么,就让它返回一个集合吧,这里就要注意了;当中心点已经是要查询的指定数值时;不要着急直接返回这个中心点;而是在这个中心点的左边以及右边去查询;找找还有没有指定的数值;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* @author by CSDN@小智RE0
* 二分查找 查找得到多个下标位置;
*/
public class BinarySearchTest02 {
//测试;
public static void main(String[] args) {
//需要查询的数组;
int[] array = {21, 3, 0, 54, 21, 67, 21};
//要找的关键字;
int num = 21;
System.out.println(" 原数组->" + Arrays.toString(array));
//需要保证数组是有序的;
Arrays.sort(array);
System.out.println("排序后的数组->" + Arrays.toString(array));
try {
List<Integer> list = BinarySearchAllIndex(array, 0, array.length, num);
System.out.println("查找的索引包括->" + list);
} catch (Exception e) {
e.printStackTrace();
}
}
/**
* 查找指定元素在已排序的数组中(由小到大排序)出现的位置;
* @param array 需要查找的数组
* @param left 左指针索引;
* @param right 右指针索引
* @param key 要查找的关键字
* @return 返回指定元素首次出现的位置;
*/
public static List<Integer> BinarySearchAllIndex(int[] array, int left, int right, int key) {
if (left > right) {
throw new RuntimeException("未找到指定的元素");
}
//定义中轴点;
int middle = (left + right) / 2;
int middleVal = array[middle];
if (middleVal > key) {
//向左递归查找;
return BinarySearchAllIndex(array, left, middle - 1, key);
} else if (middleVal < key) {
//向右递归查找;
return BinarySearchAllIndex(array, middle + 1, right, key);
} else {
List<Integer> list = new ArrayList<>();
//先把中轴点存为临时;
int temp = middle-1;
//在中轴点的左边查找;
while (temp >= 0 && array[temp] == key) {
//在中轴点的左边查找;
while (array[temp] == key) {
list.add(temp);
temp--;
}
}
//将中轴值存入;
list.add(middle);
temp = middle +1;
//在中轴点的右边查找;
while (temp <= array.length - 1 && array[temp] == key) {
while (array[temp] == key) {
list.add(temp);
temp++;
}
}
return list;
}
}
}
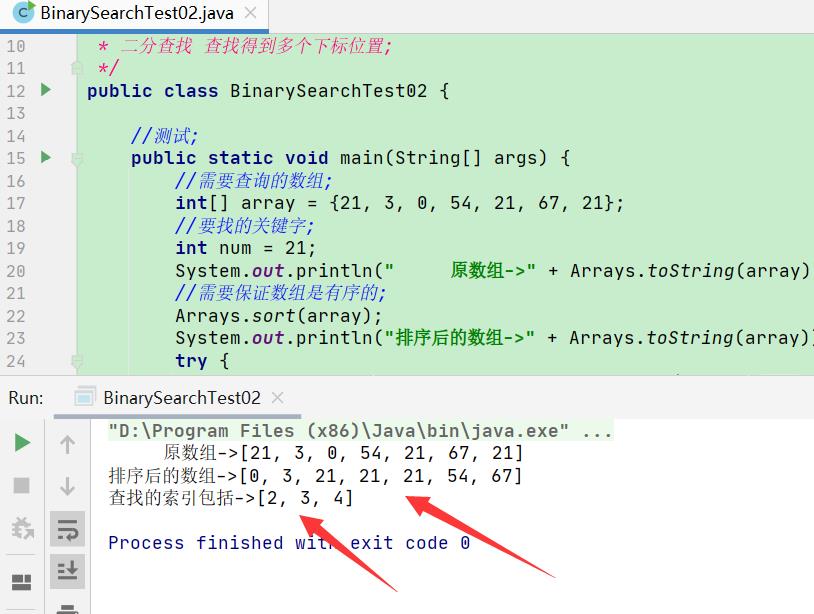
3.插值查找
可以注意到;如果说要查找的数组比较特殊;然后要查找的数在前面;这就需要递归查询好几次;
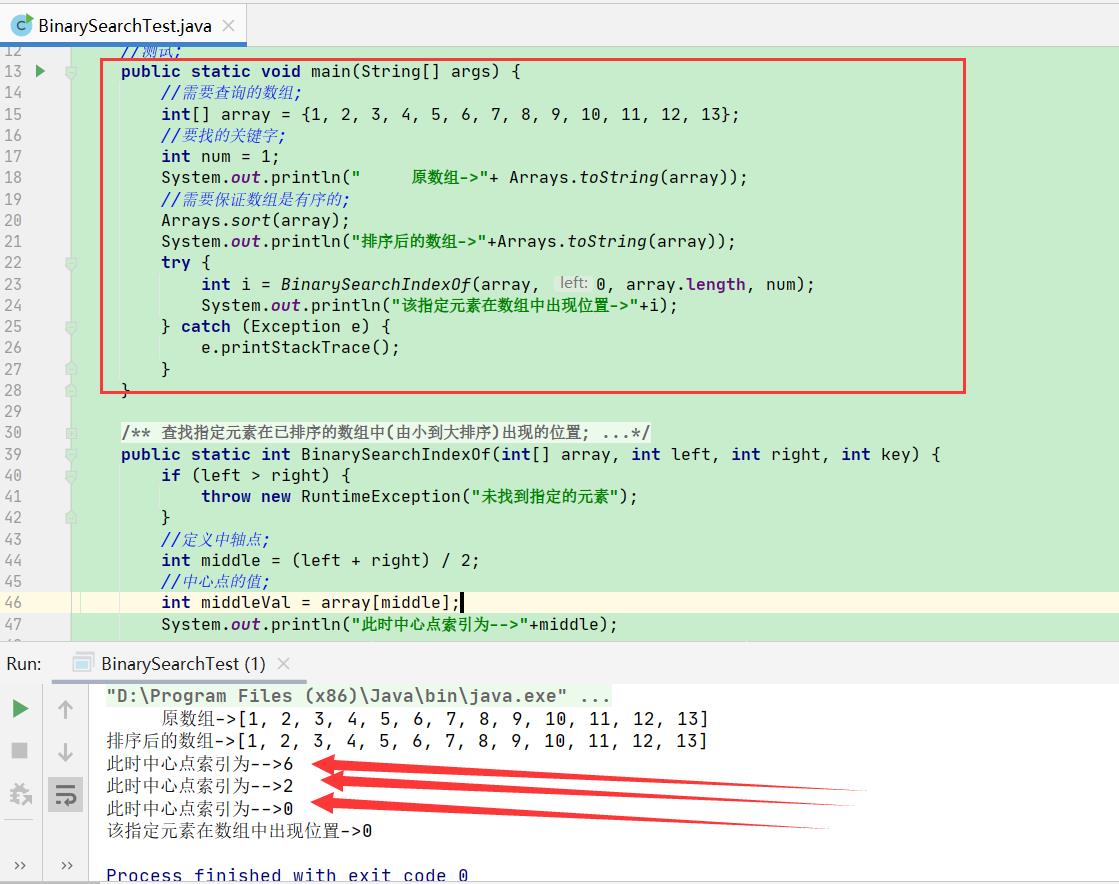
插值查找的话;是在二分查找的基础上进行优化;
就是要改变这个中心点的查找方法;

插值查找的适用场景:::>>>对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找, 速度较快
插值查找实现
/**
* @author by CSDN@小智RE0
*/
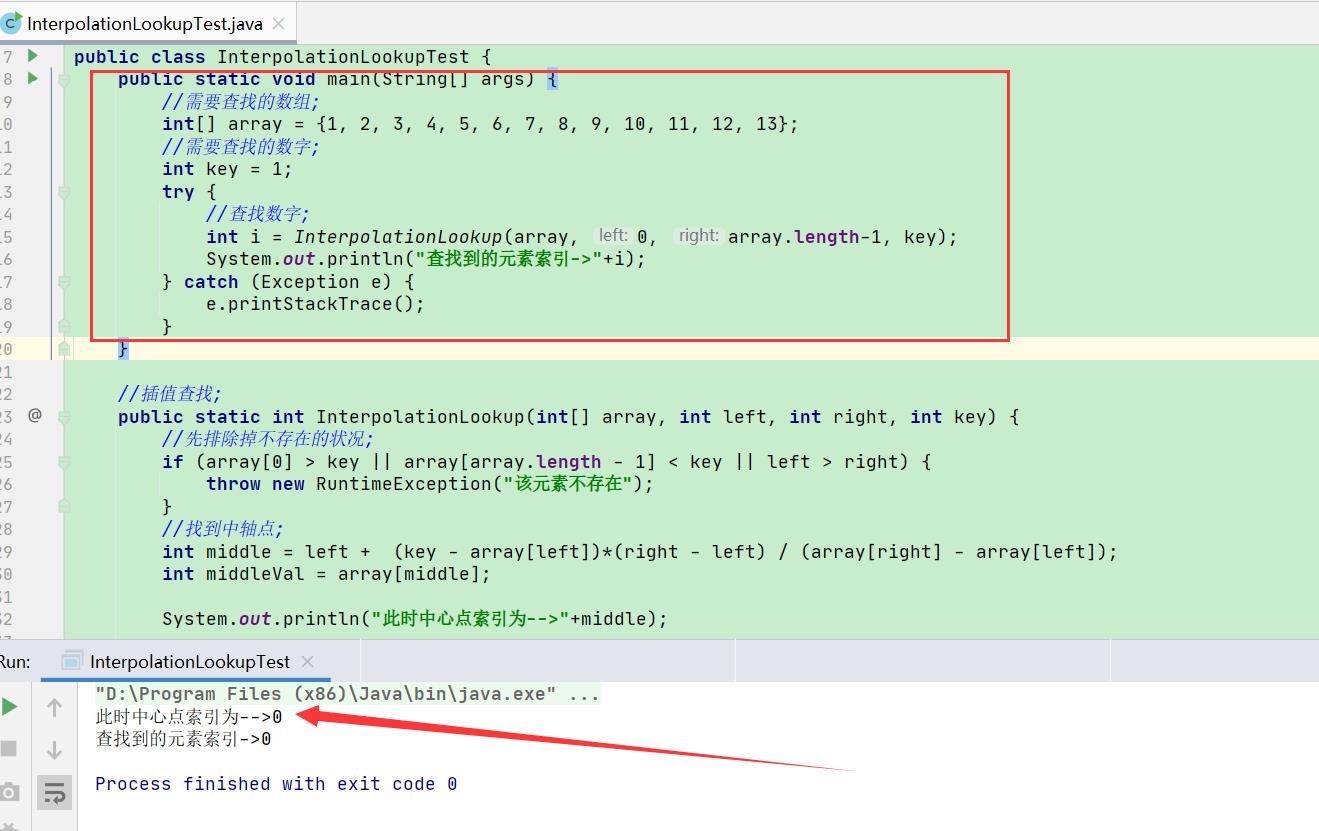
public class InterpolationLookupTest {
//测试
public static void main(String[] args) {
//需要查找的数组;
int[] array = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13};
//需要查找的数字;
int key = 1;
try {
//查找数字;
int i = InterpolationLookup(array, 0, array.length-1, key);
System.out.println("查找到的元素索引->"+i);
} catch (Exception e) {
e.printStackTrace();
}
}
//插值查找;
public static int InterpolationLookup(int[] array, int left, int right, int key) {
//先排除掉不存在的状况;
if (array[0] > key || array[array.length - 1] < key || left > right) {
throw new RuntimeException("该元素不存在");
}
//找到中轴点;
int middle = left + (key - array[left])*(right - left) / (array[right] - array[left]);
int middleVal = array[middle];
System.out.println("此时中心点索引为-->"+middle);
if(middleVal > key){
//向左递归;
return InterpolationLookup(array,left,middle-1,key);
}
else if(middleVal < key){
//向右递归;
return InterpolationLookup(array,left,middle+1,key);
}
else {
return middle;
}
}
}
测试结果
4.斐波那契查找
斐波那契查找也是在有序表中进行的查找
让查找时的中心点位于黄金分割点附近,即mid=low+F(k-1)-1(F代表斐波那契数列)

由斐波那契数列 F[k]=F[k-1]+F[k-2] 的性质,可以得到 (F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1 。
只要顺序表的长度为F[k]-1,则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段,即如
上图所示。从而中间位置为mid=low+F(k-1)-1
在进行具体实现时;
注意,由斐波那契数列的元素得到的数组长度可能会比原数组还大,那么就需要来创建一个临时的数组;但是多余的部分会被0补上,这时就得考虑把这些0的位置用原数组的最后一位元素补齐;
然后需要注意的点就是;最后通过mid=low+F(k-1)-1找到中心点了;这时要去比较这个数组的中心点的值与要查找的数; 注意中心点的推导过程;在中心点的前面有f(n-1)个元素;后面有f(n-2)个元素
具体实现过程
/**
* @author by CSDN@小智RE0
* 斐波那契查找;
*/
public class FibonacciFindTest {
//测试;
public static void main(String[] args) {
//需要查找的数组;
int[] array = {1, 3, 4, 6, 8, 20, 25};
//斐波那契查找;
System.out.println(FibonacciFind(array, 8, 10));
}
/**
* 斐波那契查找
* @param array 需要查找的数组
* @param key 要查找的元素怒
* @param fiBoLength 创建的斐波那契数组的长度
* @return 查找的元素下标
*/
public static int FibonacciFind(int[] array, int key, int fiBoLength) {
//定义最低位下标;最高位下标;
int low = 0;
int high = array.length - 1;
//斐波那契数组的索引;
int index = 0;
//创建的斐波那契数组;
int[] fiBo = getFiBo(fiBoLength);
//获取到斐波那契数组的最终索引
while (high > fiBo[index] - 1) {
index++;
}
//创建临时数组;内容为原数组的内容;长度为斐波那契数组的长度;若有空余则会用0补齐;
int[] tempArray = Arrays.copyOf(array, fiBo[index]);
System.out.println("查看临时数组=>" + Arrays.toString(tempArray));
//用原数组的最后一位替换掉后面的所有的 补位0 ;
for (int i = high + 1; i < tempArray.length; i++) {
tempArray[i] = array[high];
}
System.out.println("补位后的临时数组=>" + Arrays.toString(tempArray));
//定义中间点;
int middle = 0;
while (low <= high) {
//定义中心点;
middle = low + fiBo[index - 1] - 1;
//若要找的值较小,则去中心点前面找;
if (tempArray[middle] > key) {
high = middle - 1;
index -= 1;
} else if (tempArray[middle] < key) {
low = middle + 1;
index -= 2;
} else {
if (low > high) {
return high;
} else {
return middle;
}
}
}
return -1;
}
//获取斐波那契数组;
public static int[] getFiBo(int length) {
int[] fibonacciArray = new int[length];
fibonacciArray[0] = 1;
fibonacciArray[1] = 1;
for (int i = 2; i < fibonacciArray.length; i++) {
fibonacciArray[i] = fibonacciArray[i - 1] + fibonacciArray[i - 2];
}
return fibonacciArray;
}
}
测试结果
查看临时数组=>[1, 3, 4, 6, 8, 20, 25, 0]
补位后的临时数组=>[1, 3, 4, 6, 8, 20, 25, 25]
4
以上是关于学习数据结构笔记 ---查找算法(线性查找,二分查找,插值查找,斐波那契查找)的主要内容,如果未能解决你的问题,请参考以下文章