图论算法之AOE网

Posted 2021-09-08 踩踩踩从踩

前言

AOE网主要用在如何计算一个工程的完工时间，和优化工程方案减少工程完工时间；在实际开发过程中，会用到很多，作为现代管理中很重要的一部分，而aoe网的核心点在于如何求关键路径，这在本篇文章中会大量讲述

aoe网概念

在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，我们称之为AOE网。没有入度的顶点称为始点或源点
没有出度的顶点称为终点或汇点

如下图开始，构造一个aov网

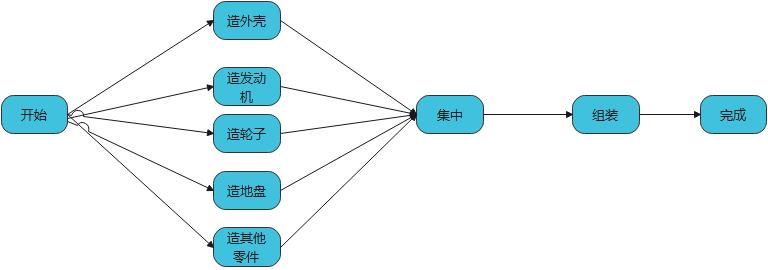
 从开始组装，到分别去造不同的零件，最后到组装完成，描述了工程的先后顺序，利用拓扑排序则能快速找到路径；但现实的工程，肯定有时间快慢之分，一定会有权重

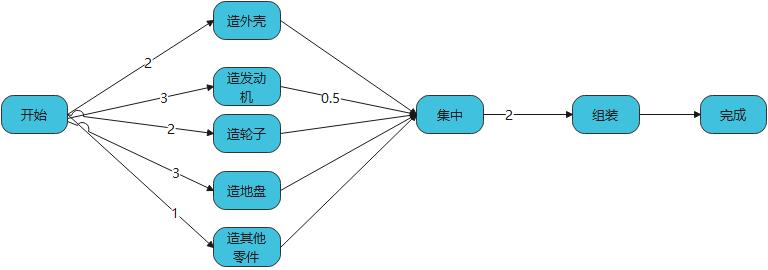
这样选择出最上的生产时间就是5.5天，并且不可能 发动机还没生产完就集中；要做优化就一定在发动机的生产优化，能优化出一些时间。

关键路径查找

从源点开始  ，汇点或终点结束

在aoe网中一般只有一个开始点和一个终点结束。

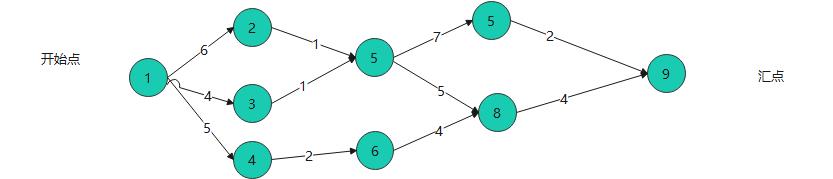
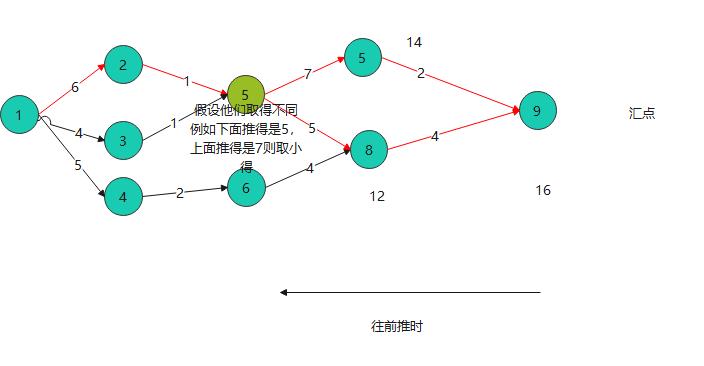
 上图所展示的情况，这是一个连续的过程，权重 则表示所需时间， 而每个顶点展示的是一个事件活动。并且aoe网一般只有一个开始点和一个汇点；找到最长路径 以下面红色表示

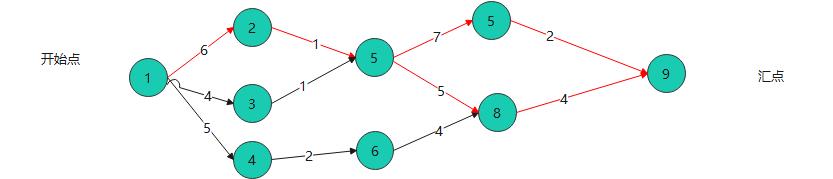
 如果其中一条关键路径被优化了，这个关键路径就有可能变化了。

• etv(Earliest Time Of Vertex) 事件最早发生时间，顶点最早发生时间
• ltv(Latest Time Of Vertex)   事件最晚发生时间，顶点最晚发生时间

结合下面的图来就是

  

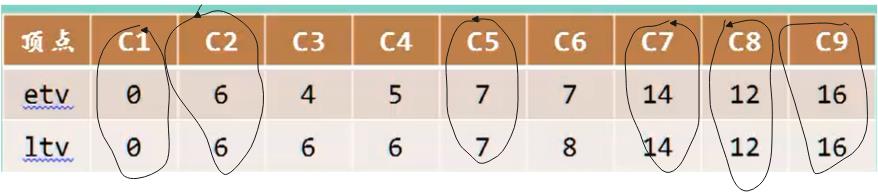
 上面的顶点 这样去理解，2的最早发生时间结合图看就是6开始，而5号则为7，因为一定要等第一件事情做完了才能发生第二件事情； 3事件的发生 就多了2个休息的事件单位。 一定是需要等待触发。 事件触发。 一定要等待最长的做完了才能做后面的。而计算机则是由后往前推。不管从哪里推。起点一定是0.

 找到这个时间只要找到相等得路径就是关键路径得顶点

 

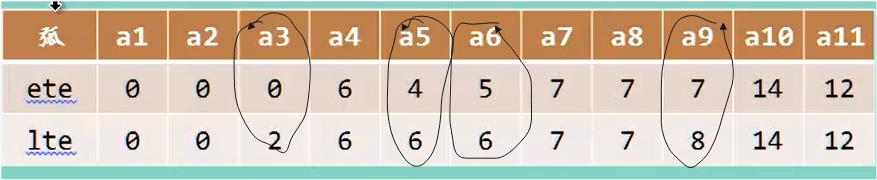
• ete(Earliest Time Of Edge)  活动最早开始时间，边最早开始时间
• lte(Latest Time Of Edge)     活动最晚开始时间，边最晚开始时间

 

 从1到3得时候，这个路径时间，其实可以改变 ，也就是说我们可以先等待两个小时在开始工作都行，都可以开始做事情。可以选择得。我们要考虑得是最早开始做得事件的时间，和最晚做事件的时间。

 有顶点还需要去算表，是通过邻接表表示

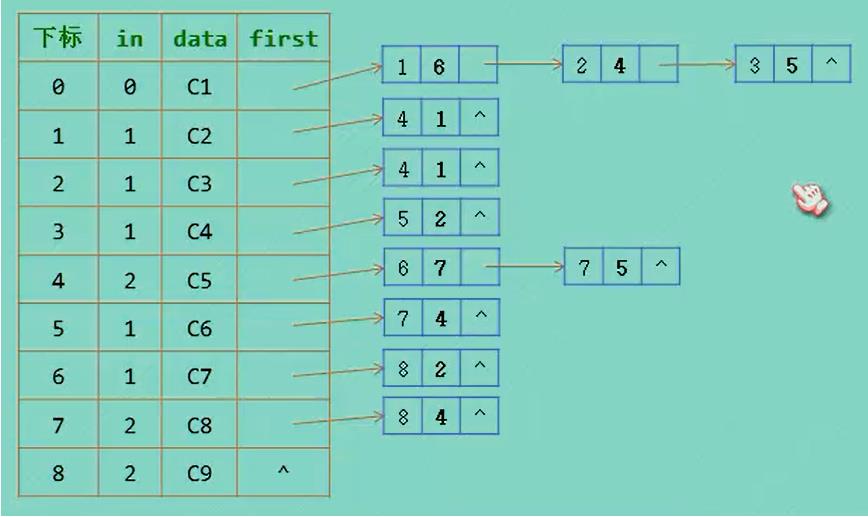
 代码实现

• 建立节点

/**
 * 边表结点
 */
class EdgeNode {
    int data;
    int weight;
    EdgeNode next;

    public EdgeNode(int data, int weight, EdgeNode next) {
        this.data = data;
        this.weight = weight;
        this.next = next;
    }

    public EdgeNode(int data, EdgeNode next) {
        this.data = data;
        this.next = next;
    }
}

/**
 * 顶点表结点
 */
class VertexNode {
    int in;//入度
    int data;
    EdgeNode first;

    public VertexNode(int in, int data, EdgeNode first) {
        this.in = in;
        this.data = data;
        this.first = first;
    }
}

然后需要把etv ltv ete lte都要计算出来

 //etv(Earliest Time Of Vertex) 事件最早发生时间，顶点最早发生时间
    int[] etv = new int[9];
    //ltv(Latest Time Of Vertex)   事件最晚发生时间，顶点最晚发生时间
    int[] ltv = new int[9];
    //ete(Earliest Time Of Edge)  活动最早开始时间，边最早开始时间
    int[] ete = new int[9];
    //lte(Latest Time Of Edge)     活动最晚开始时间，边最晚开始时间
    int[] lte = new int[9];

代码是从aov网中变化而得到

图论算法之图形变化原理、aov网与拓扑排序

需要做保存得栈和指针计算

 int[] stack2 = new int[9];
    int top2 = 0;

进行拓扑排序。  拓扑排序计算出顶点

/**
     * 拓扑排序
     */
    public void topologicalSort() {
        int top = 0;//栈顶指针
        int[] stack = new int[9];//用来存放入度为0的顶点
        //循环得到入度为0的所有顶点
        for (int i = 0; i < graphAdjList.length; i++) {
            if (graphAdjList[i].in == 0) {
                stack[++top] = i;
            }
        }
        //开始算法的逻辑
        while (top != 0) {
            int getTop = stack[top--];//出栈一个
//            System.out.print("  "+graphAdjList[getTop].data);
            //保存拓扑序列顺序
            stack2[top2++] = getTop;

            //更新当前输出节点所有的出边（后继顶点）
            for (EdgeNode e = graphAdjList[getTop].first; e != null; e = e.next) {
                int k = e.data;
                //入度减一
                graphAdjList[k].in--;
                if (graphAdjList[k].in == 0) {
                    stack[++top] = k;
                }
                //计算顶点的最早开始时间
                if ((etv[getTop] + e.weight) > etv[k]) {
                    etv[k] = etv[getTop] + e.weight;
                }

            }

        }


    }

从0开始往后找。 不断得进行比较大小；

 //计算顶点的最早开始时间
                if ((etv[getTop] + e.weight) > etv[k]) {
                    etv[k] = etv[getTop] + e.weight;
                }

最晚发生时间，取节点得最小发生时间 ，小的进行覆盖。

  //初始化ltv都为汇点时间
        for(int i=0;i<9;i++) {
            ltv[i]=etv[8];
        }

这是从后往前推，不断判断是否小于；顶点得最晚发生时间就能计算出来。

 //从汇点开始倒过来计算ltv
        while(top2>0) {
            int getTop=stack2[--top2];//从汇点开始
            for (EdgeNode e = graphAdjList[getTop].first; e != null; e = e.next) {
                int k=e.data;
                if(ltv[k]-e.weight<ltv[getTop]) {
                    ltv[getTop]=ltv[k]-e.weight;
                }
            }
        }

在计算关键路径时，已经是关键路径，其他得边不用存储。选择最短得路径。也是从后继节点出度。ete[i]=etv[i];最早开始时间。etv[k]; etv 从后往前推。

 //通过etv和ltv计算出ete和lte
        for (int i = 0; i < 9; i++) {
            for (EdgeNode e = graphAdjList[i].first; e != null; e = e.next) {
                int k=e.data;
                ete[i]=etv[i];//边的最早时间，就是顶点的最早时间
                lte[i]=ltv[k]-e.weight;//ltv[k]里面已经是选的最小的权重
                if(ete[i]==lte[i]){
                    System.out.println(graphAdjList[i].data+" "+graphAdjList[k].data+" "+e.weight);
                }

            }
        }

总结

整篇文章对aoe算法查找最短路径做了个方法及代码实现做了思路解析，如果要深入理解，还需要更一步自己实现一下