从二分类问题到KCF的公式推导

Posted 2021-09-05 jay&chuxu

KCF 算法推导

第一部分 线性可分

分类器建立

我们从一个故事开始讲起。

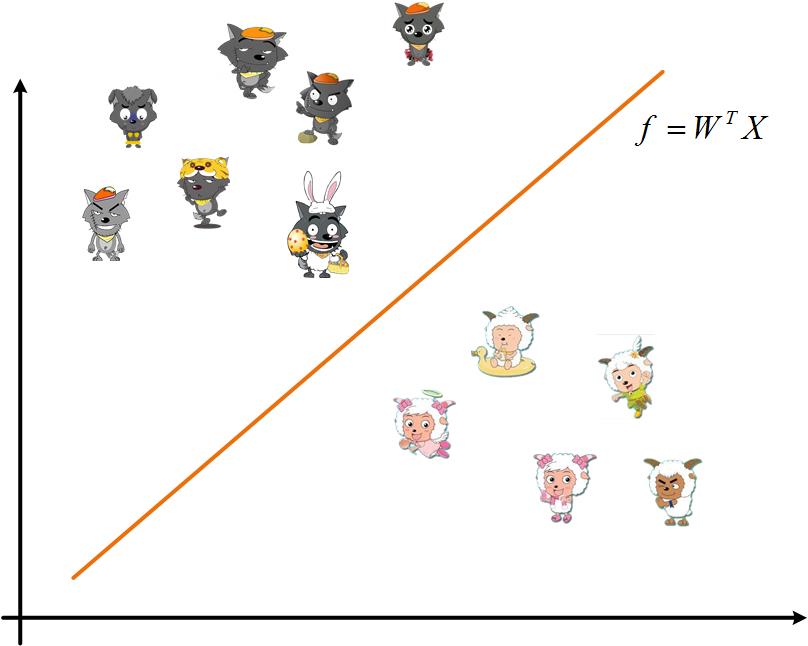
在青青草原上有两个村子，一个是羊村，一个是狼村。为了防止狼村的灰太狼们过来吃羊，在杨村要修一个栅栏。如图所示，这个栅栏修成一个直的就好。如果这条笔直的栅栏，能将两个村子分开，我们就称其为线性可分，这条栅栏，用线性函数来表示：$f(x)=W^{T}x$ 。

栅栏下方的是羊村，栅栏上方的是狼村。用函数表示就是：$f(喜羊羊)=W^T(喜羊羊)<0(羊村)$， $f(灰太狼)=W^T(灰太狼)>0(狼村)$。

可以看出，由于输入的不同，所得到的分类结果也不同。这是一个非正即负的二分类方法。假设草原上新来一只羊，那么它应该被分到羊村，否则就是羊入狼口了。

重新整理一下，在草原上已经存在的羊群 🐑 ，和狼群🐺之间，我们建了一个直线的栅栏 $f(x)$ ，将两村分开。对于新来到草原的动物，如果是羊，就根据栅栏建立的规则，划分到羊村，反之亦然。可以看出，栅栏 $f(x)$ 既是两村的划分，又是草原上动物的归类标准。假设输入的动物是 $x_i$ ，输出的分类是 $y_i$ ，他们之间的关系是：$f(x_i)=W^T{x}_i=y_i$。

判断一只动物的归属，当然要从它的生理特征来入手，比如手脚的数目，直立行走，毛发颜色，生活习性等方面，这些作为动物的特征属性，如果为每个属性都建立一个标记，假设这些属性的数量是 $d$，用数学语言表示就是：$x_i=[x_{i1},\dots ,x_{id}]$ （这里是行向量），而 $W$ 可以看成这些属性，在判断动物类别上的权重，因此也是 $d$ 维的。由于并不是没种属性对判断动物种类的重要性都相等，比如双足行走这个特征对区别喜洋洋和灰太狼来说就并没有很重要的意义。

当然，归类可能不那么准确，一个好的分类器就是要让尽可能让分类结果准确，否则就会有羊羊 🐑 被吃掉。

为了评判分类器的好坏，我们建立一个名为损失函数的东西：
$$Loss=\sum _{i=1}^n||W^T{x}_i-y_i|{|}^2+\lambda ||W|{|}^2$$
这里的 $\lambda$ 只是为了让结果中的分母不出现 0。

我们期望的结果是损失函数的结果为0，即分类器中没有损失。再来看，这个分类器中，只有一个未知数 $W$（$\lambda$是个非常小的数，不起到决定作用，可以不用考虑）。损失函数看形式，一定是个非负数（是个二次项）。那么函数的最小值，一定在导数为0的部分。先对损失函数整理一下，让它在形式上更好看一些。假设有一个向量 $c$,它的每一项 $c_i=W^T{x}_i-y_i$， 则${\sum }_{i=1}^n||W^T{x}_i-y_i|{|}^2={\sum }_{i=1}^n{c}_i^2=<c,c>=||c|{|}^2$，这里面用到了向量各元素平方和，就是向量内积，也是向量的2范数。又假设 $X=[x_1,\cdots ,x_n{]}^T$，$y=[y_1,\cdots ,y_n{]}^T$，两个都是列向量。$W,x_i$ 是 $d$ 维，即 $x_i=[x_{i1},\cdots ,x_{id}{]}^T$，$W=[w_1,\cdots ,w_d{]}^T$。
c = [ w 1 x 11 + ⋯ + w d x 1 d − y 1 ⋯ w 1 x n 1 + ⋯ + w d x n d − y n ] = [ w 1 x 11 + ⋯ + w d x 1 d ⋯ w 1 x n 1 + ⋯ + w d x n d ] − [ y 1 ⋯ y n ] = [ x 11 , ⋯   , x 1 d ⋯ x n 1 , ⋯   , x n d ] [ w 1 ⋯ w d ]

以上是关于从二分类问题到KCF的公式推导的主要内容，如果未能解决你的问题，请参考以下文章

从二分类问题到KCF的公式推导

KCF目标跟踪算法

梯度提升分类树原理推导（超级详细！）

机器学习线性分类——感知机算法（理论+图解+公式推导）

支持向量机（SVM）之数学公式详细推导

贝叶斯分类器原理及其推导