贝叶斯分类器原理及其推导

Posted 2021-04-25 中原百科

今天学术一次，就和我们目前超级火的机器学习还又什么人工智能有关，我们今天要讲的就是贝叶斯分类器的原理和推导过程，由中原百科御用学术大牛方涛投稿，呱唧呱唧！

从贝叶斯公式到贝叶斯判别准则原来线性判别分析、平方判别分析、朴素贝叶斯这么简单直白。

前方将出现大量数学公式推导证明，为防止烦躁不适，先复习一下几个重要概念。

P(A|B)表示B事件发生时A事件发生的概率，往往不能直接求，而P(B|A)求起来较为方便。在这里，为事件A发生的先验概率（prior probability）（先验概率就是指根据以往经验和分析得到的概率，可以是相对客观或者存在主观偏差的，比如抛硬币在历史上正反面的概率各是1/2，这就是在无数历史实验得到的客观准确概率）。P(A|B)为后验概率（posterior probability），即条件概率。

下面进入正题：对于常见的分类任务（classification），设表示类别的随机变量Y的样本空间{1,2,……，K}，对于样本属于第类的概率：

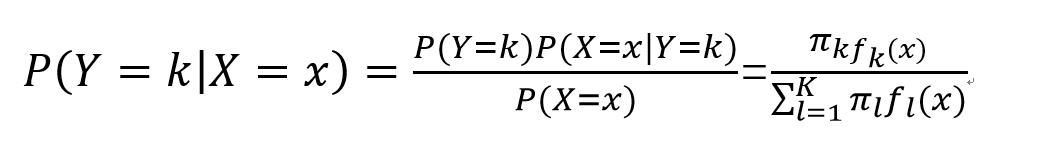
依据全概率公式将上式分母展开：

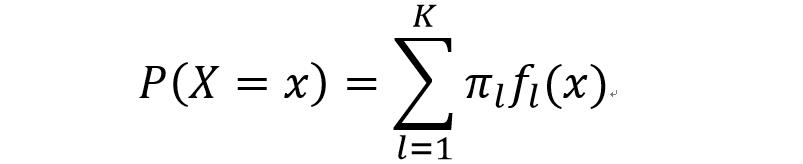
其中是随机选择的样本观测值来自第类的先验概率。

2.1.当为标量值（scalar）时，

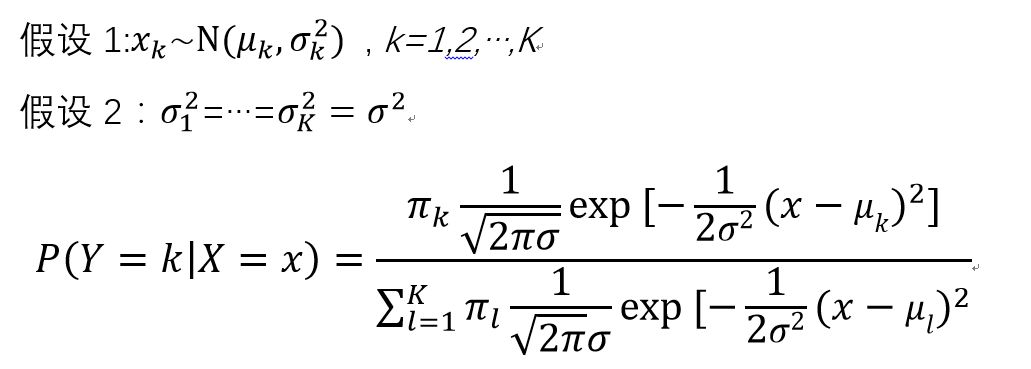
注意到分母 Y=1,2,…,K 对于都是一样的，其中参数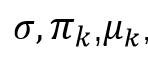都需要从样本数据集中估计得到。要确定该样本属于哪一类，只有找到使得下式分子最大的k值（防止计算溢出取对数）。

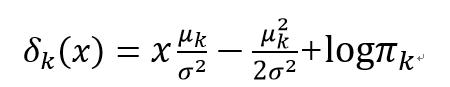
2.1 Linear Discriminant Analysis

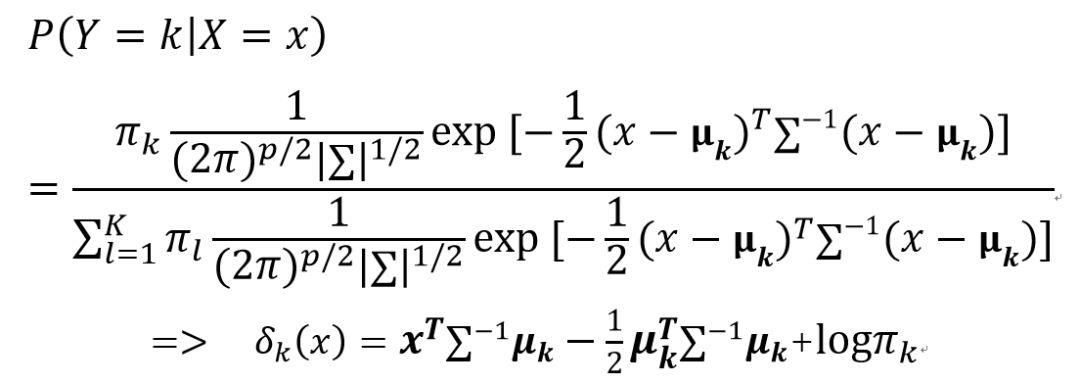
2.2Quadratic Discriminant Analysis

2.3Naïve Bayesian Classifier

2.4Laplacian correction

为了避免因训练样本不充分导致的概率估值为0，需要进行拉普拉斯修正，设为训练集D（大小为|D|）中的可能类别数，为第i属性可能的取值数，为训练集|Dk|中属于第k类的样本数

参考文献：

1.The Elements of Statistical Learning  

2.The Introduction to Statistical Learning

源代码：

注：源代码可以在后台发送 贝叶斯 获取