Java集合与数据结构——优先级队列（堆）

Posted 2021-09-05 rain67

文章目录

• 一、二叉树的顺序存储
• • 1.堆的存储方式
  • 2.下标关系
• 二、堆(heap)
• 1.概念
• 2.大/小 根堆
• • 2.1小根堆
  • 2.2大根堆
• 3.建堆操作
• • 3.1向下调整
• 4.入队操作
• • 4.1向上调整
  • 4.2push 入队的完整代码展示
• 5.出队操作
• • 5.1pop 出队代码完全展示
• 6.查看堆顶元素
• 7.TOK 问题
• • 7.1TOPK
• 8.堆排序
• 未完待续~~

文章内容介绍大纲

一、二叉树的顺序存储

1.堆的存储方式

  使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。

  一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。

这种方式的主要用法就是堆的表示。

2.下标关系

已知 双亲 (parent) 的下标，则：

左孩子(left)下标 = 2 * parent + 1;

右孩子(right)下标 = 2 * parent + 2;

已知孩子（不区分左右）(child)下标，则：

双亲(parent)下标 = (child - 1) / 2;

二、堆(heap)

1.概念

1.堆逻辑上是一棵完全二叉树

2.堆物理上是保存在数组中

3.满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆

4.反之，则是小堆，或者小根堆，或者最小堆

5.堆的基本作用是，快速找集合中的最值

2.大/小 根堆

2.1小根堆

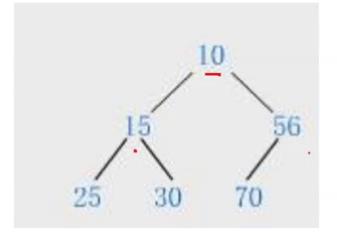
每棵树的根节点都是小于孩子节点，此时这棵树就叫做小根堆

2.2大根堆

每棵树的根节点都是大于孩子节点的，此时这棵树就叫做大根堆

  我们在说 大小根堆 时，只说了 根节点比孩子节点大，没有说 左右孩子节点谁比谁大、谁比谁小.

所以得出结论

不管是 大根堆、还是小根堆，左右孩子的大小关系是不确定的，我们只能确定根节点和孩子节点的关系.

3.建堆操作

  下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。

  根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的子树开始调整，一直调整到根节点的树，就可以调整成堆。

将一个二叉树 调整为一个 大根堆

这棵二叉树调整为 大根堆 必须将 每颗子树都调整为大根堆.

3.1向下调整

思想 步骤：

parent —> 根节点下标

child —> 孩子节点下标

1.从最后一棵子树进行调整.

2.每颗子树从根节点向下调整，如果左右孩子节点的最大值比这个根节点大，那么值互换，然后 parent 指向 child ,child = 2* parent + 1， 继续向下调整，直到 下标child 超出二叉树 范围.

3.重复第二步的操作，遍历每一颗子树，直到所有子树全部遍历完成.

代码实现：

我们对这个代码进行测试

测试堆中的结果：

时间复杂度分析：

  粗略估算，可以认为是在循环中执行向下调整，为 O(n * log(n))（了解）实际上是 O(n)

堆排序中建堆过程时间复杂度O(n)怎么来的？

4.入队操作

步骤

1.判断是否满容

2.在数组的最后插入元素

3.调整为 大/小 根堆

在这几个步骤中，前两步我们都可以完成 ，第三步我们要注意：

利用 向上调整 调整为大/ 小根堆

之前我们介绍了 向下调整

这次我们说的是向上调整，与之前向上调整的思路十分相似~~

我们来说一下 向上调整的思路

4.1向上调整

4.2push 入队的完整代码展示

5.出队操作

  为了防止破坏堆的结构，删除时并不是直接将堆顶元素删除，而是用数组的最后一个元素与堆顶元素交换，然后通过向下调整方式重新调整成堆.

思路：

1.交换 数组首尾元素

2.usedSize- -,删除最后的元素

3.利用向下调整 ，调整为大/小 根堆

5.1pop 出队代码完全展示

6.查看堆顶元素

返回 下标为0的数组元素.返回堆顶元素.

现在我们来看一个 堆的 应用

7.TOK 问题

我们在这里 提出一个问题：

在一千万个数据中找到 前 10个最大的 数据,请问如何查找

我们有 几个想法

1.基本反应，给1000万个数据排序，取10个最大 的，我们直接 Arrays.sort () ;

  这种排序方法当然也不是不可以，只不过时间复杂度非常大，在面试中写出这样的排序思路会落得下风.

2.将这1000个数据 建成一个大堆，每次将最大的取出，然后调整，取出10个即可.

  这种方法的缺点则是， 堆太大了，我们建立的堆也会是 1000万，如果这个数据更大，那么堆也会更大，每次调整的复杂度也很大.

3.建立一个大小为 K 的小堆.

以上面这个数组为例，找出这组数据中的前三个最大的元素.

3.1 将当前数据的前三个 建立为小堆

3.2 遍历剩下的元素，依次和堆顶元素进行比较. 如果当前 i 下标元素 比堆顶元素大，就把i下标入队.

  堆顶元素一定是最小的，每次都与堆顶元素进行比较，每次都将最小的那个剔除，最后遍历完，剩下的就是 最大的几个数据了嘛~

根据上面的这个 思路，我们同理可以解决很多类似的问题

7.1TOPK

找到一组数据中 最大的K个数据

建立 大小为 K 的小堆，依次遍历，最后堆中的数据 即为结果.

找到一组数据中 第K大的数据

建立 大小为 K 的小堆，依次遍历，最后堆顶元素 即为结果.

找到一组数据中 最小的K个数据

建立 大小为 K 的大堆，依次遍历，最后堆中的数据 即为结果.

找到一组数据中 第K小的数据

建立 大小为 K 的大堆，依次遍历，最后堆顶元素 即为结果.

8.堆排序

从小到大排序 —— 升序 建立大堆

从大到小排序 —— 降序 建立小堆

思路： 以升序 为 例

1.交换 数组 首尾 的元素，这样最大的堆顶元素 被放在数组的最后一个，此时 最后一个元素 已经定好序了.

2.此时从第一个到 倒数第二个再次调整，调整完后将堆顶元素 与倒数第二个元素交换，按照这样的逻辑规律，循环直到 有序.

我们以实际 例子说明…

1.首尾交换

2.向下调整

重复此操作直到全部有序

算法演示：

代码实现：

我们看一下排序的结果：

说明我们 堆排序成功运行~~

好了，堆的知识先讲到这里，希望大家多多练习~~

 下节就是关于Java中堆的使用的知识及练习了，大家敬请期待~~

Java集合与数据结构——优先级队列的使用及练习

未完待续~~