Java集合与数据结构优先级队列堆

Posted 2021-09-06 头发都哪去了

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Java集合与数据结构优先级队列堆相关的知识，希望对你有一定的参考价值。

Java集合与数据结构优先级队列【堆】

二叉树的顺序存储
- 存储方式
堆(heap)
- 操作-向下调整
堆的应用-优先级队列
堆的其他应用 TopK 问题
堆的其他应用堆排序

二叉树的顺序存储

存储方式

使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。这种方式的主要用法就是堆的表示。

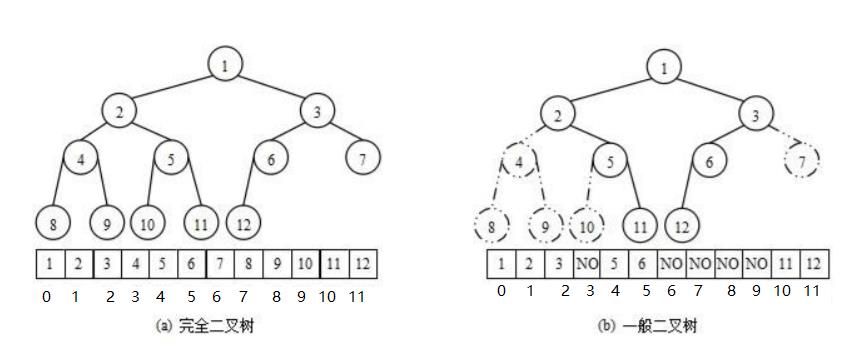
下标关系：
已知双亲(parent)的下标，则：
左孩子(left)下标 = 2 * parent + 1;
右孩子(right)下标 = 2 * parent + 2;
已知孩子（不区分左右）(child)下标，则：
双亲(parent)下标 = (child - 1) / 2;

堆(heap)

概念：

堆逻辑上是一棵完全二叉树。
堆物理上是保存在数组中。
满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆。
反之，则是小堆，或者小根堆，或者最小堆。
堆的基本作用是：快速找集合中的最值。

操作-向下调整

前提：左右子树必须已经是一个堆，才能调整。

说明：

array 代表存储堆的数组。
size 代表数组中被视为堆数据的个数。
index 代表要调整位置的下标。
left 代表 index 左孩子下标。
right 代表 index 右孩子下标。
max 代表 index 的最大值孩子的下标。

过程（以大堆为例）：

index 如果已经是叶子结点，则整个调整过程结束。

判断 index 位置有没有孩子。
因为堆是完全二叉树，没有左孩子就一定没有右孩子，所以判断是否有左孩子
因为堆的存储结构是数组，所以判断是否有左孩子即判断左孩子下标是否越界，即 left >= size 越界。

确定 left 或 right，谁是 index 的最大孩子 max。

如果右孩子不存在，则 max = left。
否则，比较 array[left] 和 array[right] 值得大小，选择大的为 max。

比较 array[index] 的值和 array[max] 的值，如果 array[index] >= array[max]，则满足堆的性质，调整结束。
否则，交换 array[index] 和 array[max] 的值。
然后因为 max 位置的堆的性质可能被破坏，所以把 max 视作 index，向下重复以上过程。

逻辑代码：

public class HeapDemo {
    public int[] elem;
    public int usedSize;

    public HeapDemo() {
        this.elem = new int[10];
    }

	//时间复杂度分析：最坏的情况即图示的情况，从根一路比较到叶子，比较的次数为完全二叉树的高度即时间复杂度为 O(log(n))
    public void adjustDown(int parent, int len) {
        int child = 2 * parent + 1;

        while (child < len) {
            if (child+1 < len && this.elem[child] < this.elem[child+1]) {
                child++;
            }
            if (this.elem[child] > this.elem[parent]) {
                int temp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = temp;
                parent = child;
                child = 2*parent+1;
            } else {
                break;
            }
        }
    }

	//时间复杂度分析：时间复杂度为 O(n * log(n))，实际上是 O(n)。
    public void createBigHeap(int[] array) {
        for (int i = 0; i < array.length; i++) {
            this.elem[i] = array[i];
            this.usedSize++;
        }

        for (int i = (this.usedSize - 1 - 1) / 2; i >= 0; i--) {
            adjustDown(i, this.usedSize);
        }
    }

    public void show() {
        for (int i = 0; i < this.usedSize; i++) {
            System.out.print(this.elem[i] + " ");
        }
        System.out.println();
    }

}

测试代码：

public class TestDemo {
    public static void main(String[] args) {
        HeapDemo heapDemo = new HeapDemo();
        int[] array = {27,15,19,18,28,34,65,49,25,37};
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
        heapDemo.createBigHeap(array);
        heapDemo.show();
    }
}

该代码的执行结果为：

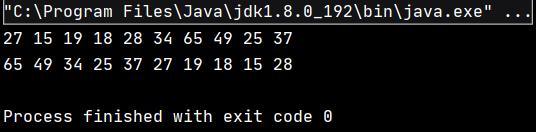
堆的应用-优先级队列

概念：
在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次高的对象。最简单的一个例子就是，在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。
在这种情况下，我们的数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。

内部原理
优先级队列的实现方式有很多，但最常见的是使用堆来构建。

操作-入队列

过程（以大堆为例）：

首先按尾插方式放入数组
比较其和其双亲的值的大小，如果双亲的值大，则满足堆的性质，插入结束
否则，交换其和双亲位置的值，重新进行 2、3 步骤
直到根结点

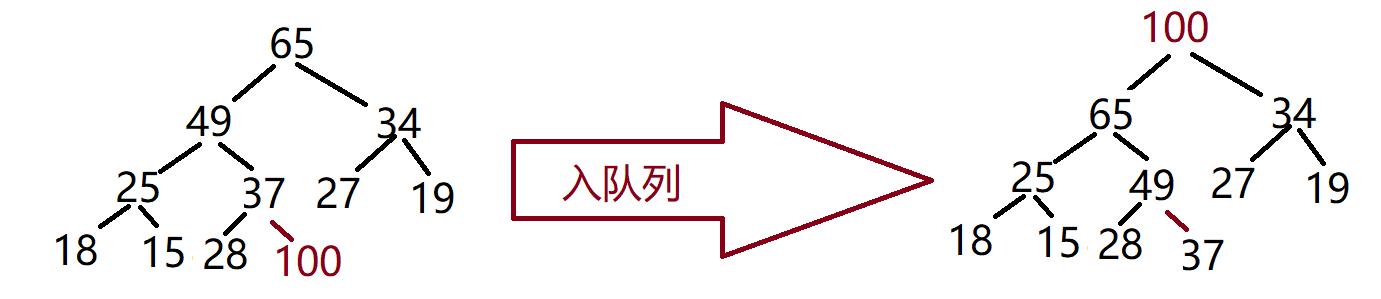
逻辑代码：

	public void adjustUp(int child) {
        int parent = (child - 1) / 2;
        while (child > 0) {
            if (this.elem[child] > this.elem[parent]) {
                int temp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = temp;
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

    public void push(int val) {
        if (isFull()) {
            this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);
        }
        this.elem[this.usedSize] = val;
        this.usedSize++;

        adjustUp(this.usedSize - 1);
    }

    public boolean isFull() {
        return this.usedSize == this.elem.length;
    }

操作-出队列

过程（以大堆为例）：

将第一个元素与最后一个元素进行交换。
删除最后一个下标
向下调整（只需要调整0号下标）

逻辑代码：

	public int poll() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空~");
        }
        int ret = this.elem[0];
        int temp = this.elem[0];
        this.elem[0] = this.elem[usedSize-1];
        this.elem[usedSize-1] = temp;
        this.usedSize--;
        adjustDown(0,this.usedSize);
        return ret;

    }

    public boolean isEmpty() {
        return this.usedSize == 0;
    }

	public void adjustDown(int parent, int len) {
        int child = 2 * parent + 1;

        while (child < len) {
            if (child + 1 < len && this.elem[child] < this.elem[child + 1]) {
                child++;
            }
            if (this.elem[child] > this.elem[parent]) {
                int temp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = temp;
                parent = child;
                child = 2 * parent + 1;
            } else {
                break;
            }
        }
    }

java 中的优先级队列

PriorityQueue implements Queue
集合框架中的PriorityQueue底层使用堆结构，因此其内部的元素必须要能够比大小，PriorityQueue采用了：Comparble和Comparator两种方式。

Comparble是默认的内部比较方式，如果用户插入自定义类型对象时，该类对象必须要实现Comparble接口，并覆写compareTo方法。
用户也可以选择使用比较器对象，如果用户插入自定义类型对象时，必须要提供一个比较器类，让该类实现Comparator接口并覆写compare方法。

堆的其他应用 TopK 问题

问题描述：从array[1, n]这n个数中，找出最大的k个数，这就是经典的TopK问题。

前k个最小的元素，建大堆；
前k个最大的元素，建小堆。

例如：从int[] array = { 27,15,19,18,28,34,65,49,25,37 };中找出最大的三个数。
逻辑代码：

public class HeapDemo {
    public int[] elem;
    public int usedSize;

    public HeapDemo() {
        this.elem = new int[10];
    }
    
    /*
    找前k个最大的元素
    创建小堆
     */
    public static void topK(int[] array,int k) {
        PriorityQueue<Integer> minHeap = new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1-o2;
            }
        });

        for (int i = 0; i < array.length; i++) {
            if (minHeap.size() < k) {
                minHeap.offer(array[i]);
            } else {
                int top = minHeap.peek();
                if (array[i] > top) {
                    minHeap.poll();
                    minHeap.offer(array[i]);
                }
            }
        }
        for (int i = 0; i < k; i++) {
            System.out.println(minHeap.poll());
        }
    }
}

调试代码：

public class TestDemo {
    public static void main(String[] args) {
        int[] array = {27,15,19,18,28,34,65,49,25,37};
        HeapDemo.topK(array,3);
    }
}

该代码的执行结果为：

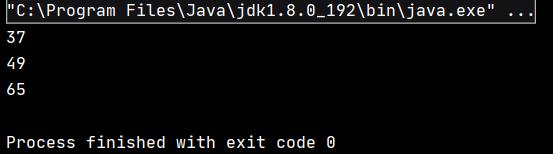
可见，该数组中最大的三个数已找到。

例如：从int[] array = { 27,15,19,18,28,34,65,49,25,37 };中找出最小的三个数。
逻辑代码：

public class HeapDemo {
    public int[] elem;
    public int usedSize;

    public HeapDemo() {
        this.elem = new int[10];
    }
    
    /*
    找前k个最小的元素
    创建大堆
     */
    public static void minTopK(int[] array,int k) {
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2-o1;
            }
        });

        for (int i = 0; i < array.length; i++) {
            if (maxHeap.size() < k) {
                maxHeap.offer(array[i]);
            } else {
                Integer top = maxHeap.peek();
                if (top != null) {
                    if (array[i] < top) {
                        maxHeap.poll();
                        maxHeap.offer(array[i]);
                    }
                }
            }
        }
        for (int i = 0; i < k; i++) {
            System.out.println(maxHeap.poll());
        }
    }
}

调试代码：

public class TestDemo {
    public static void main(String[] args) {
        int[] array = {27,15,19,18,28,34,65,49,25,37};
        HeapDemo.minTopK(array,3);
    }
}

该代码的执行结果为：

可见，该数组中最小的三个数已找到。

堆的其他应用堆排序

基本原理是选择排序，只是不在使用遍历的方式查找无序区间的最大的数，而是通过堆来选择无序区间的最大的数。

注意：排升序要建大堆；排降序要建小堆。

时间复杂度：不管是最好的情况还是最坏的情况都是O(n * log(n)) 。
空间复杂度：O(1)。

以排升序为例，逻辑代码：

public class HeapDemo {
    public int[] elem;
    public int usedSize;

    public HeapDemo() {
        this.elem = new int[10];
    }


    public void adjustDown(int parent, int len) {
        int child = 2 * parent + 1;

        while (child < len) {
            if (child + 1 < len && this.elem[child] < this.elem[child + 1]) {
                child++;
            }
            if (this.elem[child] > this.elem[parent]) {
                int temp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = temp;
                parent = child;
                child = 2 * parent + 1;
            } else {
                break;
            }
        }
    }
	
	public void createBigHeap(int[] array) {
        for (int i = 0; i < array.length; i++) {
            this.elem[i] = array[i];
            this.usedSize++;
        }

        for (int i = (this.usedSize - 1 - 1) / 2; i >= 0; i--) {
            adjustDown(i, this.usedSize);
        }
    }

	public void show() {
        for (int i = 0Java集合与数据结构 优先级队列堆
 Java集合与数据结构 优先级队列堆
 Java集合数据结构——优先级队列 (堆PriorityQueue)
 Java集合与数据结构——优先级队列的使用及练习
 数据结构 Java数据结构 ---- 堆(优先级队列)
 第五节：Java集合框架之优先级队列PriorityQueue（堆）

Java集合与数据结构 优先级队列堆

Java集合与数据结构 优先级队列【堆】