编译原理构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 8.)(笔记)一元运算符正负(+,-)
Posted Dontla
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了编译原理构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 8.)(笔记)一元运算符正负(+,-)相关的知识,希望对你有一定的参考价值。
【编译原理】让我们来构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 8.)
今天我们将讨论一元运算符,即一元加(+)和一元减(-)运算符。
今天的很多资料都基于上一篇文章中的资料,因此如果您需要复习,请返回第 7 部分并再次阅读。请记住:重复是所有学习之母。
话虽如此,这就是你今天要做的:
- 扩展语法以处理一元加号和一元减号运算符
- 添加一个新的UnaryOp AST节点类
- 扩展解析器以生成具有UnaryOp 节点的AST
- 扩展解释器并添加一个新的visit_UnaryOp方法来解释一元运算符
让我们开始吧,好吗?
到目前为止,我们只使用了二元运算符(+、-、*、/),即对两个操作数进行运算的运算符。
那什么是一元运算符呢?一元运算符是 仅对一个操作数进行运算的运算符。
以下是一元加号和一元减号运算符的规则:
- 一元减号 (-) 运算符产生其数值操作数的否定
- 一元加号 (+) 运算符生成其数字操作数而无需更改
- 一元运算符的优先级高于二元运算符 +、-、* 和 /
在表达式“+ - 3”中,第一个’+‘运算符代表一元加运算,第二个’-'运算符代表一元减运算。表达式“+ - 3”等价于“+ (- (3))”,它等于-3。也可以说表达式中的-3是一个负整数,但在我们的例子中,我们将其视为一元减运算符,其中 3 作为其正整数操作数:
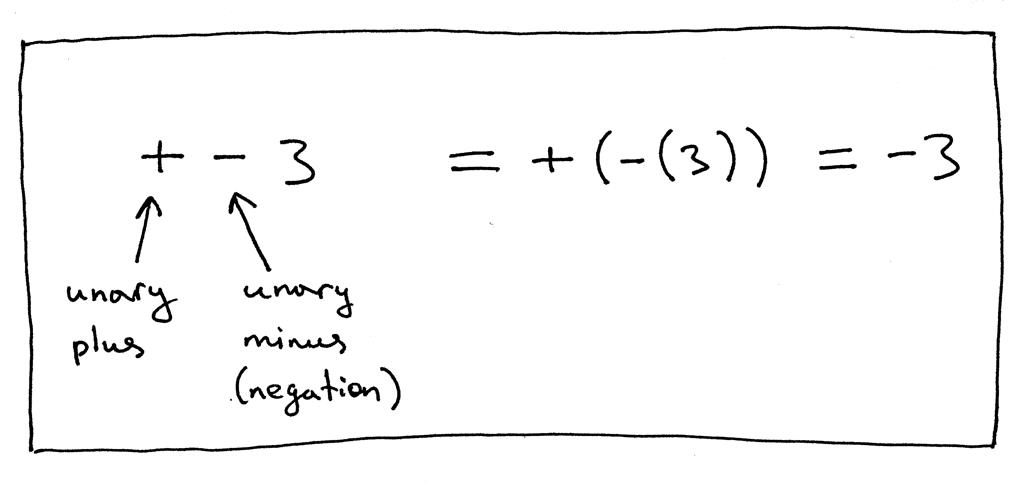
我们再来看看另一个表达式,“5 - - 2”:
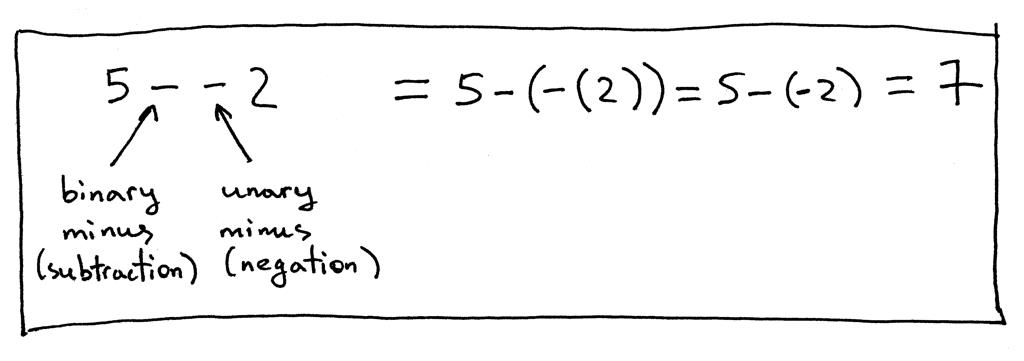
在表达式“5 - - 2”中,第一个’-‘代表二元减法运算,第二个’-'代表一元减法运算,即否定。
还有一些例子:
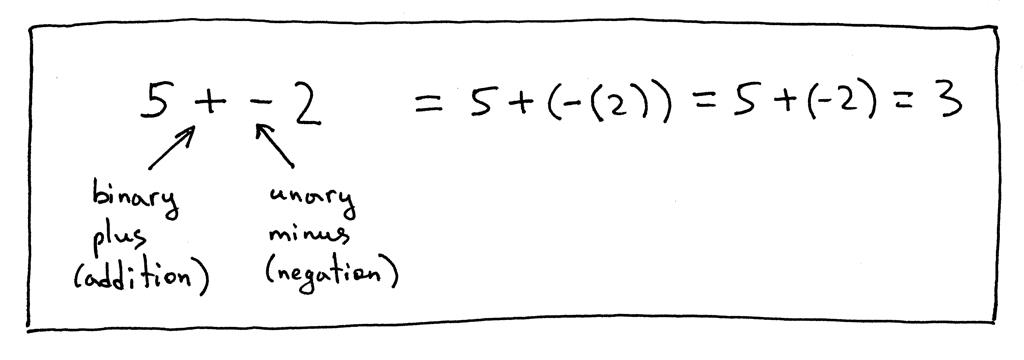
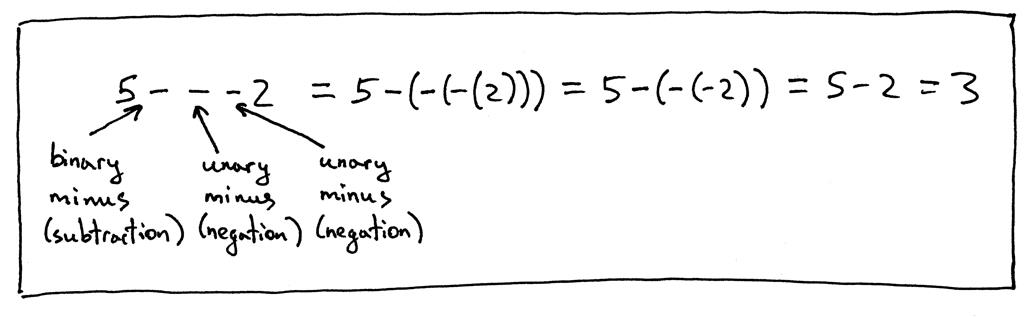
现在让我们更新我们的语法以包含一元加号和一元减号运算符。我们将修改因子规则并在那里添加一元运算符,因为一元运算符的优先级高于二元 +、-、* 和 / 运算符。
这是我们当前的因子 规则:

这是我们处理一元加和一元减运算符的更新因子规则:

如您所见,我将因子规则扩展为引用自身,这使我们能够推导出诸如“- - - + - 3”之类的表达式,这是一个带有许多一元运算符的合法表达式。
这是现在可以使用一元加号和一元减号运算符派生表达式的完整语法:

下一步是添加一个AST节点类来表示一元运算符。
这个会做:
class UnaryOp(AST):
def __init__(self, op, expr):
self.token = self.op = op
self.expr = expr
构造函数接受两个参数:op,它代表一元运算符标记(加号或减号)和expr,它代表一个AST 节点。
我们更新的语法对factor规则进行了更改,因此这就是我们要在解析器中修改的内容 -factor方法。我们将添加代码来处理方法“(PLUS | MINUS)factor”分治:
def factor(self):
"""factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN"""
token = self.current_token
if token.type == PLUS:
self.eat(PLUS)
node = UnaryOp(token, self.factor())
return node
elif token.type == MINUS:
self.eat(MINUS)
node = UnaryOp(token, self.factor())
return node
elif token.type == INTEGER:
self.eat(INTEGER)
return Num(token)
elif token.type == LPAREN:
self.eat(LPAREN)
node = self.expr()
self.eat(RPAREN)
return node
现在我们需要扩展Interpreter类并添加一个visit_UnaryOp方法来解释一元节点:
def visit_UnaryOp(self, node):
op = node.op.type
if op == PLUS:
return +self.visit(node.expr)
elif op == MINUS:
return -self.visit(node.expr)
向前!
让我们手动为表达式“5 - - - 2”构建一个AST并将其传递给我们的解释器以验证新的visit_UnaryOp方法是否有效。以下是从 Python shell 执行此操作的方法:
>>> from spi import BinOp, UnaryOp, Num, MINUS, INTEGER, Token
>>> five_tok = Token(INTEGER, 5)
>>> two_tok = Token(INTEGER, 2)
>>> minus_tok = Token(MINUS, '-')
>>> expr_node = BinOp(
... Num(five_tok),
... minus_tok,
... UnaryOp(minus_token, UnaryOp(minus_token, Num(two_tok)))
... )
>>> from spi import Interpreter
>>> inter = Interpreter(None)
>>> inter.visit(expr_node)
3
从视觉上看,上面的AST树是这样的:
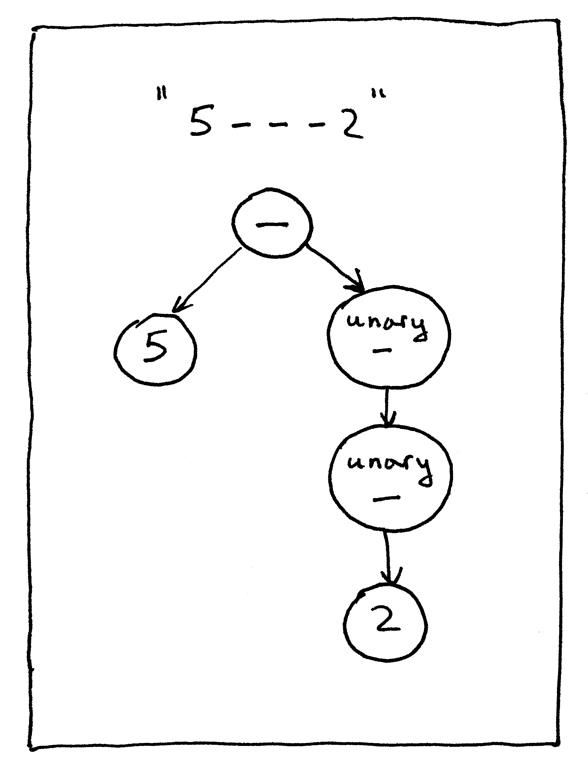
直接从GitHub下载本文解释器的完整源代码。亲自尝试一下,看看您更新的基于树的解释器是否正确评估包含一元运算符的算术表达式。
这是一个示例会话:
$ python spi.py
spi> - 3
-3
spi> + 3
3
spi> 5 - - - + - 3
8
spi> 5 - - - + - ( 3 + 4 ) - +2
10
我还更新了genastdot.py实用程序来处理一元运算符。以下是为带有一元运算符的表达式生成的AST图像的一些示例:
$ python genastdot.py "- 3" > ast.dot && dot -Tpng -o ast.png ast.dot
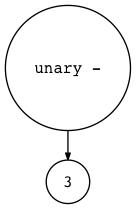
$ python genastdot.py "+ 3" > ast.dot && dot -Tpng -o ast.png ast.dot
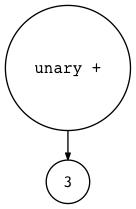
$ python genastdot.py "5 - - - + - 3" > ast.dot && dot -Tpng -o ast.png ast.dot
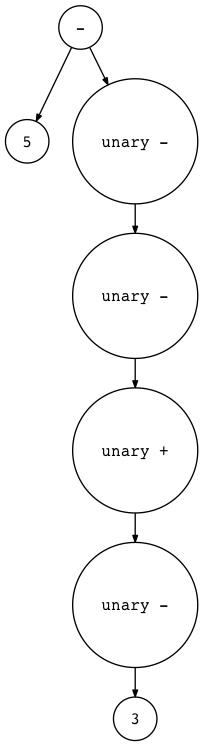
$ python genastdot.py "5 - - - + - (3 + 4) - +2" \\
> ast.dot && dot -Tpng -o ast.png ast.dot
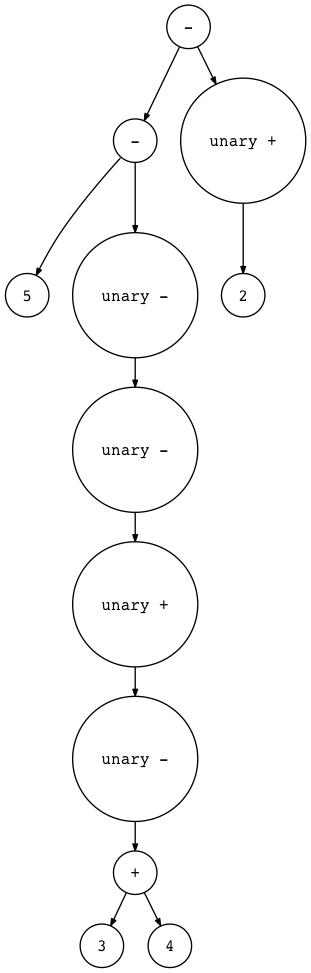
这是给你的一个新练习:
- 安装Free Pascal,编译并运行testunary.pas,并验证结果与使用spi 解释器生成的结果相同。
这就是今天的全部内容。在下一篇文章中,我们将处理赋值语句。请继续关注,很快就会见到你。
C语言代码(作者没提供完整的python代码,关键的改动提供了,在上面,完整的python代码这里略掉)
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
#include <string.h>
#include<math.h>
#define flag_integer 0
#define flag_plus 1
#define flag_minus 2
#define flag_multiply 3
#define flag_divide 4
#define flag_LPAREN 5
#define flag_RPAREN 6
#define flag_plus_sign 7
#define flag_minus_sign 8
#define flag_EOF 7
void error() {
printf("程序不对劲!\\n");
exit(-1);
}
//给字符数组赋值
void StrAssign(char* T, const char* chars)
{
int i;
for (i = 0; i < strlen(chars); i++)
T[i] = *(chars + i);
T[i] = '\\0';
}
struct Token
{
int type;
int value;
};
//Token初始化函数
struct Token* mallocToken(int type, int value) {
struct Token* token = (Token*)malloc(sizeof(Token));
if (NULL != token) {
token->type = type;
token->value = value;
return token;
}
else
error();
}
//树的节点
struct BinOpOrNum
{
struct BinOpOrNum* left;
struct Token* op_or_num;
struct BinOpOrNum* right;
};
//树结点初始化函数
struct BinOpOrNum* mallocOpOrNum(struct BinOpOrNum* left, struct Token* op_or_num, struct BinOpOrNum* right) {
struct BinOpOrNum* node = (BinOpOrNum*)malloc(sizeof(BinOpOrNum));
if (NULL != node) {
node->left = left;
node->op_or_num = op_or_num;
node->right = right;
return node;
}
else
error();
}
struct Lexer
{
char* text;
int pos;
};
struct Parser
{
struct Lexer* lexer;
struct Token current_token;
};
struct Interpreter
{
struct Parser* parser;
};
void skip_whitespace(struct Lexer* le) {
while (le->text[le->pos] == ' ') {
le->pos++;
}
}
//判断Interpreter中当前pos是不是数字
int is_digital(char c) {
if (c >= '0' && c <= '9')
return 1;
else
return 0;
}
void advance(struct Lexer* le) {
le->pos++;
}
char current_char(struct Lexer* le) {
return(le->text[le->pos]);
}
//获取数字token的数值(把数字字符数组转换为数字)
int integer(struct Lexer* le) {
char temp[20];
int i = 0;
while (is_digital(le->text[le->pos])) {
temp[i] = le->text[le->pos];
i++;
advance(le);
}
int result = 0;
int j = 0;
int len = i;
while (j < len) {
result += (temp[j] - '0') * pow(10, len - j - 1);
j++;
}
return result;
}
void get_next_token(struct Parser* par) {
//先跳空格,再判断有没有结束符
if (current_char(par->lexer) == ' ')
skip_whitespace(par->lexer);
if (par->lexer->pos > (strlen(par->lexer->text) - 1)) {
par->current_token = { flag_EOF, NULL };
return;
}
char current = current_char(par->lexer);
if (is_digital(current)) {
par->current_token = { flag_integer, integer(par->lexer) };
return;
}
if (current == '+') {
par->current_token = { flag_plus, NULL };
advance(par->lexer);
return;
}
if (current == '-') {
par->current_token = { flag_minus, NULL };
advance(par->lexer);;
return;
}
if (current == '*') {
par->current_token = { flag_multiply, NULL };
advance(par->lexer);;
return;
}
if (current == '/') {
par->current_token = { flag_divide, NULL };
advance(par->lexer);;
return;
}
if (current == '(') {
par->current_token = { flag_LPAREN, NULL };
advance(par->lexer);;
return;
}
if (current == ')') {
par->current_token = { flag_RPAREN, NULL };
advance(par->lexer);;
return;
}
error();//如果都不是以上的字符,则报错并退出程序
}
int eat(struct Parser* par, int type) {
int current_token_value = par->current_token.value;
if (par->current_token.type == type) {
get_next_token(par);
return current_token_value;
}
else {
error();
}
}
//遍历树
int visit_BinOp(struct BinOpOrNum* node) {
if (node->op_or_num->type == flag_plus)
return visit_BinOp(node->left) + visit_BinOp(node->right);
else if (node->op_or_num->type == flag_minus)
return visit_BinOp(node->left) - visit_BinOp(node->right);
else if (node->op_or_num->type == flag_multiply)
return visit_BinOp(node->left) * visit_BinOp(node->right);
else if (node->op_or_num->type == flag_divide)
return visit_BinOp(node->left) / visit_BinOp(node->right);
else if (node->op_or_num->type == flag_integer)
return node->op_or_num->value;
else if (node->op_or_num->type == flag_plus_sign)
return visit_BinOp(node->right);
else if (node->op_or_num->type == flag_minus_sign)
return (-1) * visit_BinOp(node->right);
}
struct BinOpOrNum* expr(struct Parser* par);//expr定义在后面,在这里要声明才能使用
//判断数字或括号或正负号(加减号后出现的正负号)
struct BinOpOrNum* factor(struct Parser* par) {
if (par->current_token.type == flag_plus) {
eat(par, flag_plus);
struct Token* token = mallocToken(flag_plus_sign , NULL);
struct BinOpOrNum* node = mallocOpOrNum(NULL, token, factor(par));
return node;
}
else if (par->current_token.type == flag_minus) {
eat(par, flag_minus);
struct Token* token = mallocToken(flag_minus_sign, NULL);
struct BinOpOrNum* node = mallocOpOrNum(NULL, token, factor(par));
return node;
}
else if (par->current_token.type == flag_integer) {
struct Token* token = mallocToken(par->current_token.type, par->current_token.value);
eat(par, flag_integer);
struct BinOpOrNum* node = mallocOpOrNum(NULL, token, NULL);
return node;
}
else if (par->current_token.type == flag_LPAREN) {
eat(par, flag_LPAREN);
//遇到括号先吃掉,然后回到expr
struct BinOpOrNum* node = expr(par);
eat(par, flag_RPAREN);
return node;
}
}
//判断乘除
struct BinOpOrNum* term(struct Parser* par) {
struct BinOpOrNum* node = factor(par);
while (par->current_t以上是关于编译原理构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 8.)(笔记)一元运算符正负(+,-)的主要内容,如果未能解决你的问题,请参考以下文章
编译原理构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 9.)(笔记)语法分析(未完,先搁置了!)
编译原理让我们来构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 2.)(python/c/c++版)(笔记)
编译原理让我们来构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 6.)(python/c/c++版)(笔记)
编译原理让我们来构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 4.)(python/c/c++版)(笔记)
编译原理让我们来构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 3.)(python/c/c++版)(笔记)
编译原理构建一个简单的解释器(Let’s Build A Simple Interpreter. Part 7.)(笔记)解释器 interpreter 解析器 parser 抽象语法树AST(代码片