Python数据结构系列《线性表》——知识点讲解+代码实现
Posted Vax_Loves_1314
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python数据结构系列《线性表》——知识点讲解+代码实现相关的知识,希望对你有一定的参考价值。
灵魂拷问:为什么要学数据结构?
数据结构,直白地理解,就是研究数据的存储方式。数据存储只有一个目的,即为了方便后期对数据的再利用。因此,数据在计算机存储空间的存放,决不是胡乱的,这就要求我们选择一种好的方式来存储数据,而这也是数据结构的核心内容。
可以说,数据结构是一切编程的基本。学习数据结构是学习一种思想:如何把现实问题转化为计算机语言的表示。
对于学计算机的朋友来说,学习数据结构是基本功。而对于非计算机专业,但是未来想往数据分析、大数据方向发展、或者在Python的使用上能有一个大的跨越的朋友来说,学习数据结构是一种非常重要的逻辑思维能力的锻炼,在求职、职业发展、问题解决等方面都能有潜移默化的大帮助。
tips:本文介绍的知识只是作为一个引子,供小伙伴们参考学习,在学习过程中如果遇到问题,一定要多去搜索相关博客、文章、书籍等其他资料,作为补充学习。
废话不多说,我们开整!
1.线性表(线性存储结构)
线性表是数据结构中最简单的数据存储结构,可以理解为“线性的表”。线性,是说数据在逻辑结构上具有线性关系。将具有“一对一”关系的数据“线性”地存储到物理空间中,这种存储结构就称为线性存储结构(简称线性表)。
1.1 线性表基本介绍
线性表,数据结构中最简单的一种存储结构,专门用于存储逻辑关系为"一对一"的数据。基于数据在实际物理空间中的存储状态,又可细分为顺序表(顺序存储结构)和链表(链式存储结构)。
线性表,全名为线性存储结构。使用线性表存储数据的方式可以这样理解,即"把所有数据用一根线儿串起来,再存储到物理空间中"。

如图 1 所示,这是一组具有“一对一”关系的数据,我们接下来采用线性表将其储存到物理空间中。
首先,用“一根线儿”把它们按照顺序“串”起来,如图 2 所示:
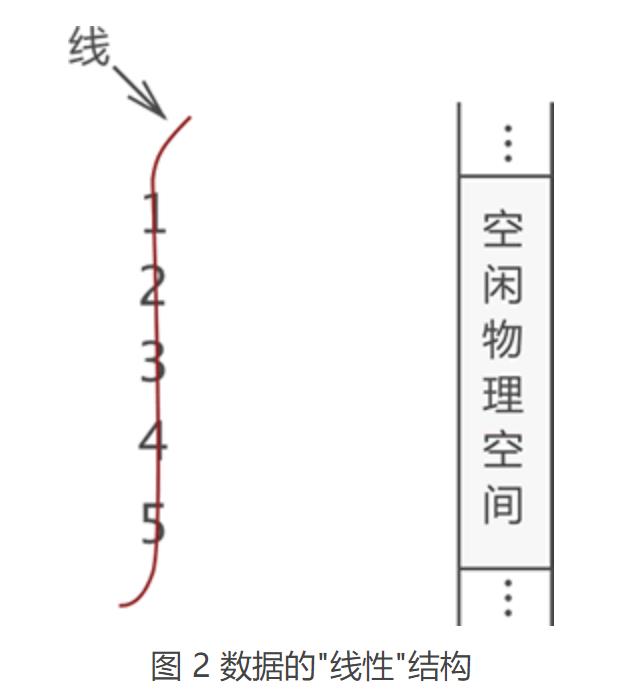
图 2 中,左侧是“串”起来的数据,右侧是空闲的物理空间。把这“一串儿”数据放置到物理空间,我们可以选择以下两种方式,如图 3 所示。
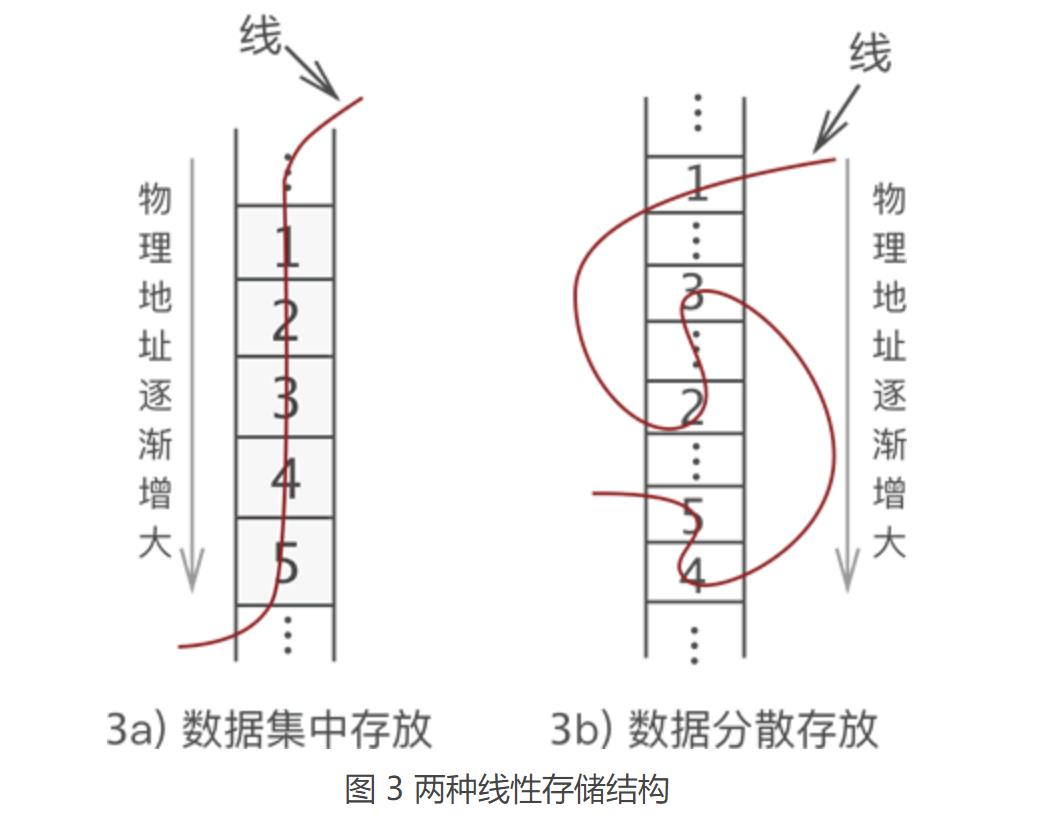
图 3a) 是多数人想到的存储方式,而图 3b) 却少有人想到。我们知道,数据存储的成功与否,取决于是否能将数据完整地复原成它本来的样子。如果把图 3a) 和图 3b) 线的一头扯起,你会发现数据的位置依旧没有发生改变(和图 1 一样)。因此可以认定,这两种存储方式都是正确的。
将具有**“一对一”关系的数据“线性”地存储到物理空间中**,这种存储结构就称为线性存储结构(简称线性表)。
使用线性表存储的数据,如同向数组中存储数据那样,要求数据类型必须一致,也就是说,线性表存储的数据,要么全部都是整形,要么全部都是字符串。一半是整形,另一半是字符串的一组数据无法使用线性表存储。
1.2 顺序存储结构和链式存储结构
图 3 中我们可以看出,线性表存储数据可细分为以下 2 种:
(1) 如图 3a) 所示,将数据依次存储在连续的整块物理空间中,这种存储结构称为顺序存储结构(简称顺序表);
(2)如图 3b) 所示,数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系,这种存储结构称为链式存储结构(简称链表);
也就是说,线性表存储结构可细分为顺序存储结构和链式存储结构。
1.3 前驱和后继
数据结构中,一组数据中的每个个体被称为“数据元素”(简称“元素”)。例如,图 1 显示的这组数据,其中 1、2、3、4 和 5 都是这组数据中的一个元素。
另外,对于具有“一对一”逻辑关系的数据,我们一直在用“某一元素的左侧(前边)或右侧(后边)”这样不专业的词,其实线性表中有更准确的术语:
某一元素的左侧相邻元素称为“直接前驱”,位于此元素左侧的所有元素都统称为“前驱元素”;
某一元素的右侧相邻元素称为“直接后继”,位于此元素右侧的所有元素都统称为“后继元素”;
以图 1 数据中的元素 3 来说,它的直接前驱是 2 ,此元素的前驱元素有 2 个,分别是 1 和 2;同理,此元素的直接后继是 4 ,后继元素也有 2 个,分别是 4 和 5。如下图所示:
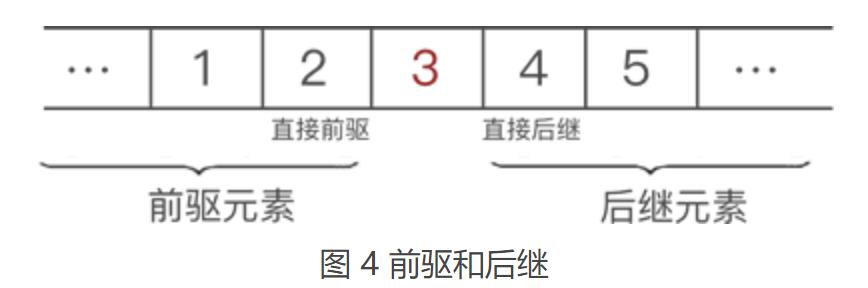
2. 顺序表(顺序存储结构)
2.1 顺序表基本介绍
顺序表,全名顺序存储结构,是线性表的一种。通过《什么是线性表》一节的学习我们知道,线性表用于存储逻辑关系为“一对一”的数据,顺序表自然也不例外。
不仅如此,顺序表对数据的物理存储结构也有要求。顺序表存储数据时,会提前申请一整块足够大小的物理空间,然后将数据依次存储起来,存储时做到数据元素之间不留一丝缝隙。
例如,使用顺序表存储集合 {1,2,3,4,5},数据最终的存储状态如图1所示:
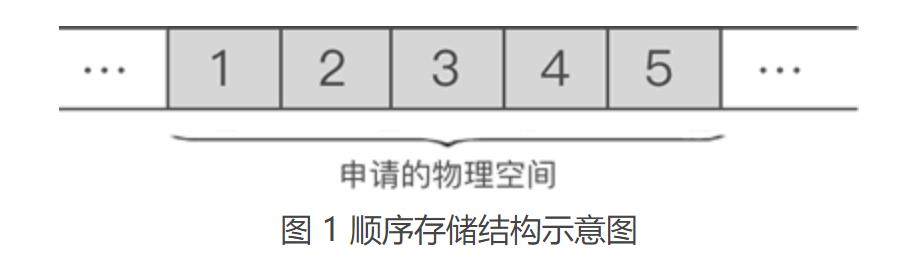
由此我们可以得出,将“具有 ‘一对一’ 逻辑关系的数据按照次序连续存储到一整块物理空间上”的存储结构就是顺序存储结构。
通过观察图 1 中数据的存储状态,我们可以发现,顺序表存储数据同数组非常接近。其实,顺序表存储数据使用的就是数组。
2.2 顺序表基本操作之插入元素
向已有顺序表中插入数据元素,根据插入位置的不同,可分为以下 3 种情况:
① 插入到顺序表的表头;
② 在表的中间位置插入元素;
③ 尾随顺序表中已有元素,作为顺序表中的最后一个元素;
虽然数据元素插入顺序表中的位置有所不同,但是都使用的是同一种方式去解决,即:通过遍历,找到数据元素要插入的位置,然后做如下两步工作:
① 将要插入位置元素以及后续的元素整体向后移动一个位置;
② 将元素放到腾出来的位置上;
例如,在 {1,2,3,4,5} 的第 3 个位置上插入元素 6,实现过程如下:
① 遍历至顺序表存储第 3 个数据元素的位置,如图 1 所示:
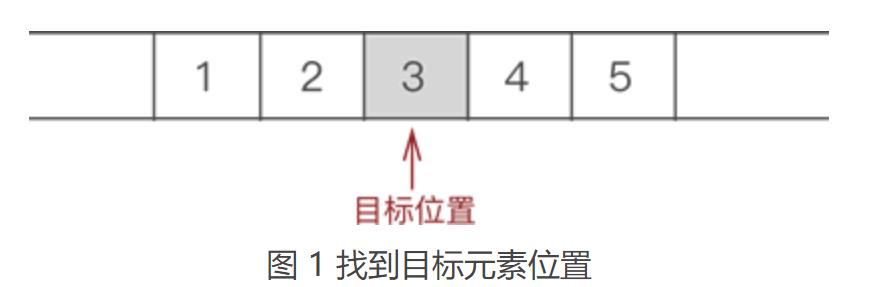
② 将元素 3 以及后续元素 4 和 5 整体向后移动一个位置,如图 2 所示:
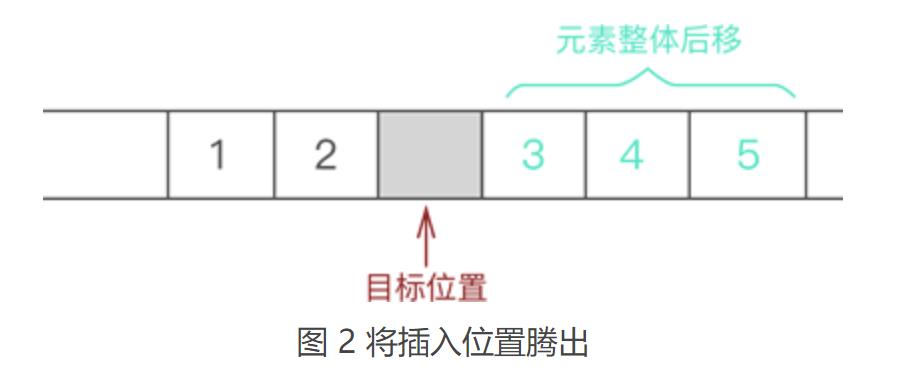
③ 将新元素 6 放入腾出的位置,如图 3 所示:
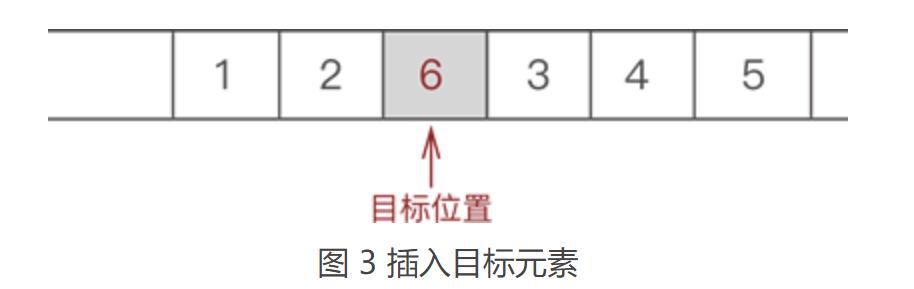
2.3 顺序表基本操作之删除元素
从顺序表中删除指定元素,实现起来非常简单,只需找到目标元素,并将其后续所有元素整体前移 1 个位置即可。
【注】:后续元素整体前移一个位置,会直接将目标元素删除,可间接实现删除元素的目的。
例如,从 {1,2,3,4,5} 中删除元素 3 的过程如图 4 所示:
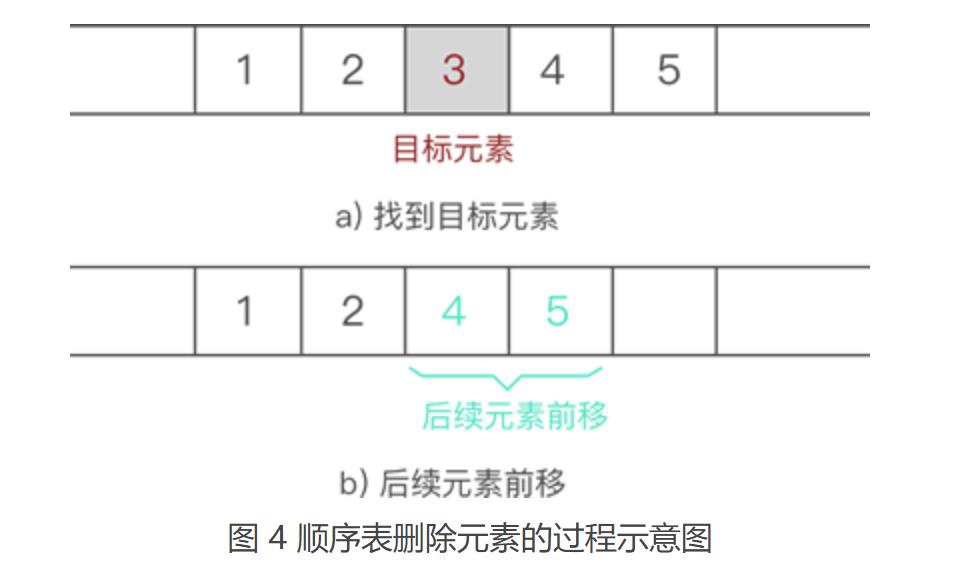
2.4 顺序表基本操作之查找元素
顺序表中查找目标元素,可以使用多种查找算法实现,比如说二分查找算法、插值查找算法等。
2.5 顺序表基本操作之更改元素
顺序表更改元素的实现过程是:
(1)找到目标元素;
(2)直接修改该元素的值;
关于顺序表Python编程实现代码可参考↓(个人编写,仅供参考,欢迎提出宝贵建议)
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2021/7/20 15:42
# @Author : vaxtiandao
# @File : ds_1.py
import random
random.seed(10)
# 定义顺序表的类
class SqList():
# 初始化
def __init__(self, length):
self.length = length # 先指定数组的长度
self.sqlist = [random.randint(1, 100) for j in range(length)] # 生成length长度的随机数组
# 输出所有元素
def ShowList(self):
return self.sqlist
# 遍历所有元素
def ErgodicList(self):
for i in range(self.length):
print("第{}个元素值为{}".format(i+1, self.sqlist[i]))
# 取值
def GetElem(self, i):
# 首先判断插入的位置是否在合法范围内(1,length)
if i < 1 or i > self.length:
pass
return False
return self.sqlist[i-1] # 在的话,直接返回值
# 查找
def LocateElem(self, e):
# 通过循环遍历列表,找到列表中等于e的元素,返回其位置索引
for j in range(self.length):
if e == self.sqlist[j]:
return j
break
# 否则,输出一句话:"列表中不存在查找的元素",然后返回False
print("列表中不存在查找的元素")
# 插入
def ListInsert(self, i, e):
# 首先判断插入的位置是否在合法范围内(1,length),不在的话,直接返回False
if i < 1 or i > self.length:
return False
return self.sqlist.insert(i,e) # 列表中有insert()函数
# 删除
def ListDelete(self, i):
# 首先判断插入的位置是否在合法范围内(1,length),不在的话,直接返回False
if i < 1 or i > self.length:
return False
return self.sqlist.pop(i) # 列表有个pop()函数,该函数会返回删除的值
# 定义一个顺序表对象
length = 10
my_sqlist = SqList(length)
print("初始化的顺序表:", my_sqlist)
print("_________________________________________________")
# 输出所有参数
mylist = my_sqlist.ShowList()
print("输出所有参数:", mylist)
print("_________________________________________________")
# 调用遍历函数
print("遍历顺序表")
my_sqlist.ErgodicList()
print("_________________________________________________")
# 插入
print("插入前的列表:{}".format(my_sqlist.ShowList()))
i = 4 # 插入的索引位置
e = 10 # 插入的值
my_sqlist.ListInsert(i, e) # 在指定索引位置插入值
print("插入后的顺序表:{}".format(my_sqlist.ShowList()))
print("_________________________________________________")
# 删除
i = 5 # 删除的索引位置
print("删除前的顺序表:{}".format(my_sqlist.ShowList()))
my_sqlist.ListDelete(i) # 删除i索引所在位置上的值
print("删除后的顺序表:{}".format(my_sqlist.ShowList()))
print("_________________________________________________")
# 取值
index = 8 # 这里代表的是第10个数,不是位置索引为10的数,索引+1才是具体第几个数;
value = my_sqlist.GetElem(index)
if value:
print("顺序表中第{}个数等于{}".format(index, value))
print("_________________________________________________")
# 查找
e = 55 # 要查找的数
index = my_sqlist.LocateElem(e)
if index:
print("元素{}在顺序表中的索引为{}".format(e, index))
如下是实现效果:
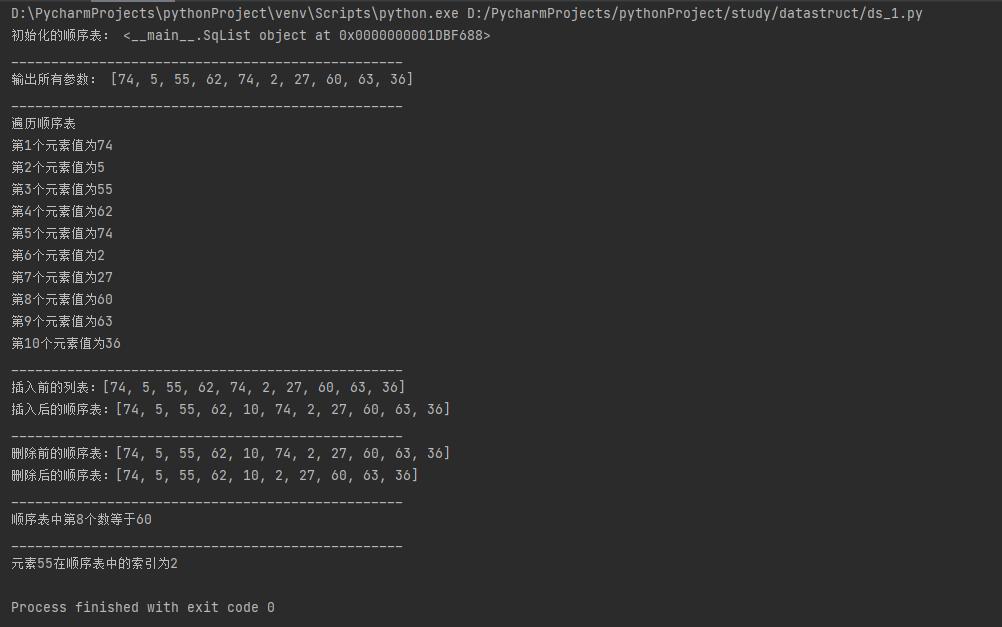
关于顺序表基本操作的C语言代码,可以看这:顺序表的基本操作
3. 单链表,链式存储结构
3.1 单链表基本介绍
前面详细地介绍了顺序表,本节给大家介绍另外一种线性存储结构——链表。
链表,别名链式存储结构或单链表,用于存储逻辑关系为 “一对一” 的数据。与顺序表不同,链表不限制数据的物理存储状态,换句话说,使用链表存储的数据元素,其物理存储位置是随机的。
例如,使用链表存储 {1,2,3},数据的物理存储状态如图1所示:
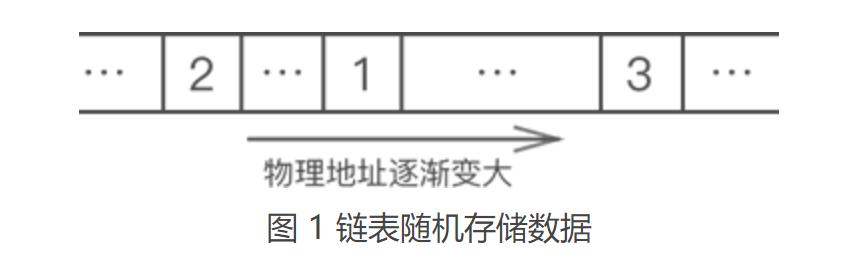
我们看到,上图根本无法体现出各数据之间的逻辑关系。对此,链表的解决方案是,每个数据元素在存储时都配备一个指针,用于指向自己的直接后继元素。如图2所示:
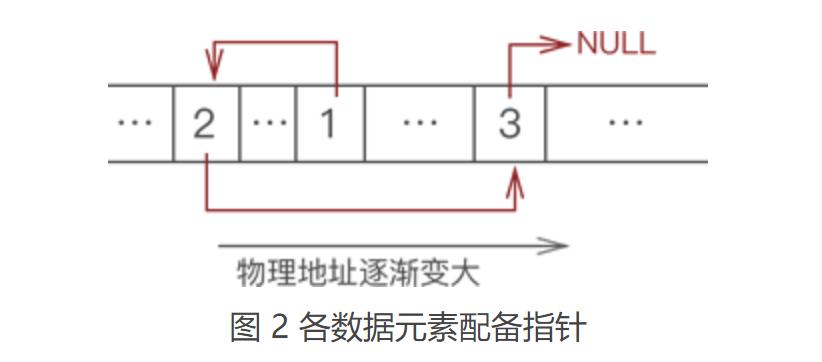
像图2这样,数据元素随机存储,并通过指针表示数据之间逻辑关系的存储结构就是链式存储结构。
3.2 链表的节点
从上图可以看到,链表中每个数据的存储都由以下两部分组成:
(1)数据元素本身,其所在的区域称为数据域;
(2) 指向直接后继元素的指针,所在的区域称为指针域;
即链表中存储各数据元素的结构如图3所示:

上图所示的结构在链表中称为节点。也就是说,链表实际存储的是一个一个的节点,真正的数据元素包含在这些节点中,如图4所示:
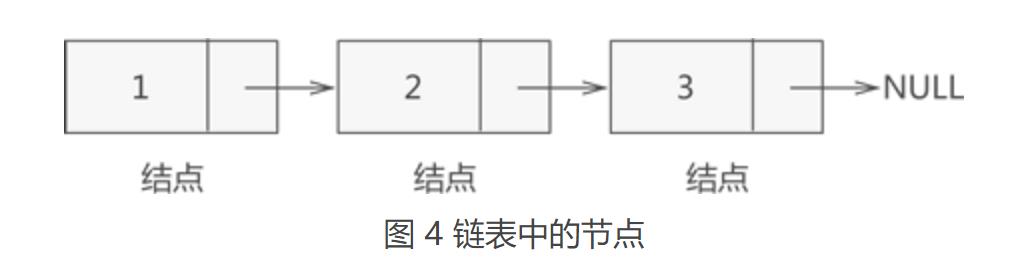
3.3 头节点,头指针和首元节点
其实,图 4 所示的链表结构并不完整。一个完整的链表需要由以下几部分构成:
1. 头指针:一个普通的指针,它的特点是永远指向链表第一个节点的位置。很明显,头指针用于指明链表的位置,便于后期找到链表并使用表中的数据;
2. 节点:链表中的节点又细分为头节点、首元节点和其他节点:
(1)头节点:其实就是一个不存任何数据的空节点,通常作为链表的第一个节点。对于链表来说,头节点不是必须的,它的作用只是为了方便解决某些实际问题;
(2)首元节点:由于头节点(也就是空节点)的缘故,链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓,没有实际意义;
(3)其他节点:链表中其他的节点;
因此,一个存储 {1,2,3} 的完整链表结构如图5所示:
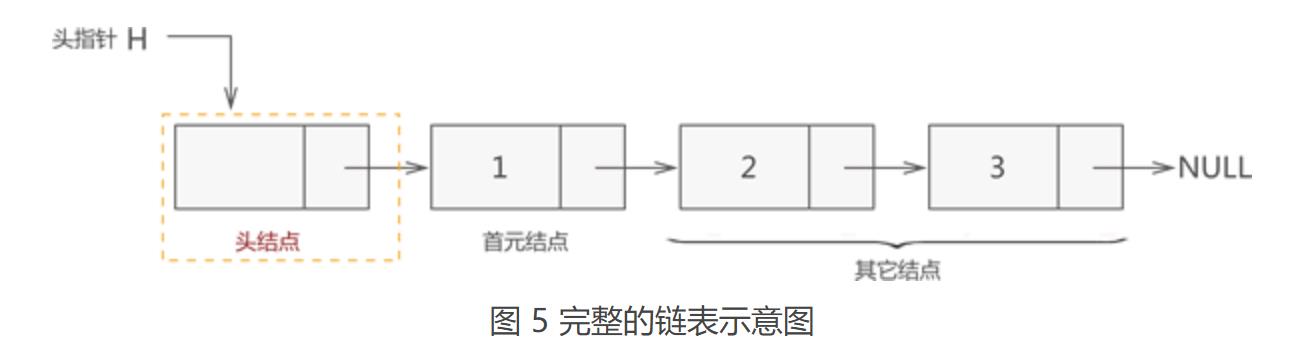
【注】:链表中有头节点时,头指针指向头节点;反之,若链表中没有头节点,则头指针指向首元节点。
明白了链表的基本结构,下面我们来学习如何创建一个链表。
3.4 链表的创建(初始化)
创建一个链表需要做如下工作:
1. 声明一个头指针(如果有必要,可以声明一个头节点);
2. 创建多个存储数据的节点,在创建的过程中,要随时与其前驱节点建立逻辑关系;
3.5 单链表基本操作
本节将详细介绍对链表的一些基本操作,包括对链表中数据的添加、删除、查找(遍历)和更改。
插入元素
同顺序表一样,向链表中增添元素,根据添加位置不同,可分为以下 3 种情况:
(1)插入到链表的头部(头节点之后),作为首元节点;
(2)插入到链表中间的某个位置;
(3)插入到链表的最末端,作为链表中最后一个数据元素;
虽然新元素的插入位置不固定,但是链表插入元素的思想是固定的,只需做以下两步操作,即可将新元素插入到指定的位置:
(1)将新结点的 next 指针指向插入位置后的结点;
(2)将插入位置前结点的 next 指针指向插入结点;
例如,我们在链表 {1,2,3,4} 的基础上分别实现在头部、中间部位、尾部插入新元素 5,其实现过程如图 1 所示:
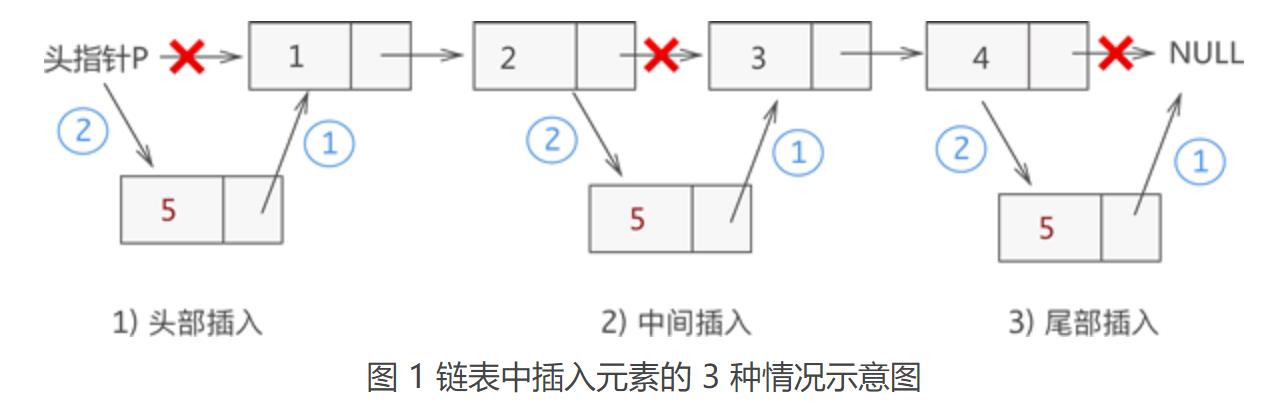
从图中可以看出,虽然新元素的插入位置不同,但实现插入操作的方法是一致的,都是先执行步骤 1 ,再执行步骤 2。
【注意】:链表插入元素的操作必须是先步骤 1,再步骤 2;反之,若先执行骤步 2,除非再添加一个指针,作为插入位置后续链表的头指针,否则会导致插入位置后的这部分链表丢失,无法再实现步骤 1
删除元素
从链表中删除指定数据元素时,实则就是将存有该数据元素的节点从链表中摘除,但作为一名合格的程序员,要对存储空间负责,对不再利用的存储空间要及时释放。因此,从链表中删除数据元素需要进行以下 2 步操作:
(1)将结点从链表中摘下来;
(2)手动释放掉结点,回收被结点占用的存储空间;
其中,从链表上摘除某节点的实现非常简单,只需找到该节点的直接前驱节点 temp,例如,从存有 {1,2,3,4} 的链表中删除元素 3,则此代码的执行效果如图 2 所示:
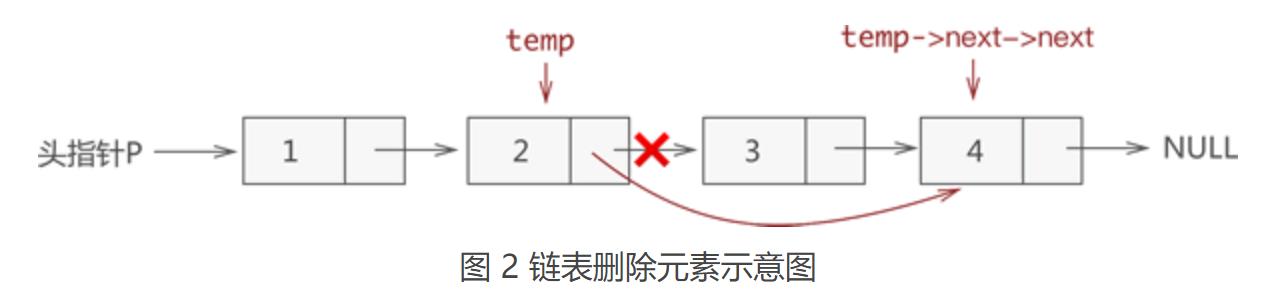
查找元素
在链表中查找指定数据元素,最常用的方法是:从表头依次遍历表中节点,用被查找元素与各节点数据域中存储的数据元素进行比对,直至比对成功或遍历至链表最末端的 NULL(比对失败的标志)。
注意,遍历有头节点的链表时,需避免头节点对测试数据的影响,因此在遍历链表时,建立使用上面代码中的遍历方法,直接越过头节点对链表进行有效遍历。
更新元素
更新链表中的元素,只需通过遍历找到存储此元素的节点,对节点中的数据域做更改操作即可。
关于链表Python编程实现代码可参考↓(个人编写,仅供参考,欢迎提出宝贵建议)
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2021/7/21 17:12
# @Author : vaxtiandao
# @File : ds_12.py
# 单向链表的实现
# 每个节点包含两部分,数据区和指向下个节点的链接
# 单向列表:每个节点包含两部分:数据区与链接区(指向下一个节点),最后一个元素的链接区为None
# 单向列表只要找到头节点,就可以访问全部节点
# 定义结点类,包含两个成员:结点元素值和指向下一结点的指针
class SingleNode():
# 结点类初始化
def __init__(self, item):
self.item = item # item存放结点的数值
self.next = None # 下一指针指向
# 定义单链表
class SingleLinkList():
# 链表类初始化
def __init__(self):
self.head = None
# 判断链表是否为空
def is_empty(self):
return self.head == None
# 输出链表长度
def get_length(self):
return len(self.travel())
# 遍历整个链表
def travel(self):
# 思路就是先判断链表是否为空
# 为空直接返回None,
# 不为空的话,就先定义一个列表,然后通过next指针从头指针开始遍历,依次将结点存储的值加入列表中,直到下一指针指向为空,则停止遍历;
if self.is_empty():
return None
else:
curlist = []
cur = self.head
while cur != None:
curlist.append(cur.item)
cur = cur.next
return curlist
# 头插法创建单链表
def add(self, newItem):
node = SingleNode(newItem)
node.next = self.head # 指针变换
self.head = node
# 尾插法
def append(self, newItem):
node = SingleNode(newItem)
if self.is_empty():
return self.add(newItem)
# 从头结点开始遍历
nod = self.head
while nod.next != None: # 当下一个结点的next为None时,停止遍历// 注:跟网上不一样,回头用尾插法新建单链表试试
nod = nod.next
nod.next = node
# 指定位置添加元素
def insert(self, pos, newItem): # 在指定pos位置上添加newItem元素
# 链表的插入需要分几种情况
# 第一步 判断pos是否在合理范围内,如果不在,则直接终止
# 第二步 判断pos是否在第一个,如果是则采用头插法
# 第三步 如果pos在最后一个,则采用尾插法
# 第四步 如果既不在头,也不再尾,则通过循环遍历到pos位置,再用Insert插入
node = SingleNode(newItem)
cur = self.head
count = 0
if pos == 0:
return self.add(newItem)
elif pos < (self.get_length()):
while count < pos - 1:
cur = cur.next
count += 1
node.next = cur.next
cur.next = node
elif pos == (self.get_length()):
return self.append(newItem)
else:
return '输入的位置有误,请确认'
# 删除指定位置上的结点
def remove(self, pos):
# 第一步 判断给定的pos是否再合理范围内
# 第二步 通过循环,遍历到pos位置,遍历期间通过next指针依次指向下一结点
# 第三步 找到指定位置的结点后,通过nod.next = nod.next.next删除
cur = self.head
count = 0
if 1 <= pos < (self.get_length()):
while count < pos - 1:
cur = cur.next
count += 1
cur.next = cur.next.next
elif pos == 0:
self.head = cur.next
else:
return '输入的位置有误,请确认'
# 查找指定位置的结点值
def find(self, pos):
cur = self.head
count = 0
if 0 <= pos < (self.get_length()):
while count < pos:
cur = cur.next
count += 1
return cur.item
else:
return '输入的位置有误,请确认'
# 更新链表中某个位置的值
def update(self, pos, newItem):
cur = self.head
count = 0
if 0 <= pos < (self.get_length()):
while count < pos:
cur = cur.next
count += 1
cur.item = newItem
else:
return '输入的位置有误,请确认'
## 清空链表
def clear(self):
self.head = None
singlelinklist = SingleLinkList() # 实例化对象
print("初始化单链表:",singlelinklist)
print("________________________________________________________________________________________________")
print("判断单链表是否为空:",singlelinklist.is_empty())
print("________________________________________________________________________________________________")
# 添加数据
import random
for i in range(10):
singlelinklist.add(random.randint(1,100))
# 遍历数据
singlelinklist.travel()
print("遍历单链表:",singlelinklist.travel())
print("________________________________________________________________________________________________")
print("判断单链表是否为空:",singlelinklist.is_empty())
print("________________________________________________________________________________________________")
# 末尾添加数据
singlelinklist.append(10)
print("末尾添加元素后的单链表遍历结果:", singlelinklist.travel())
print("________________________________________________________________________________________________")
# 开头添加数据
singlelinklist.add(1)
print("开头添加元素后的单链表遍历结果:", singlelinklist.travel())
print("________________________________________________________________________________________________")
# 查看数据长度
print("单链表长度:",singlelinklist.get_length())
print("________________________________________________________________________________________________")
# 指定位置插入数据,位置从0开始
singlelinklist.insert(1, 13)
print("插入数据后的遍历单链表:", singlelinklist.travel())
print("________________________________________________________________________________________________")
# 删除指定位置数据
singlelinklist.remove(0)
print("删除数据后的遍历单链表:", singlelinklist.travel())
print("________________________________________________________________________________________________")
# 更新指定位置数据
singlelinklist.update(2,2)
print("更新数据后的遍历单链表:", singlelinklist.travel())
print("________________________________________________________________________________________________")
# 清空所有数据
singlelinklist.clear()
print("清空数据后的遍历单链表:", singlelinklist.travel())
print("________________________________________________________________________________________________")
如下是代码实现效果:
 Python数据结构系列☀️《查找排序-基础知识》——知识点讲解+代码实现☀️
Python数据结构系列☀️《查找排序-基础知识》——知识点讲解+代码实现☀️
大厂算法系列编码手写顺序表相关功能,线性结构核心知识点详细剖析
Python数据结构系列☀️《树与二叉树-基础知识》——知识点讲解+代码实现☀️
Python数据结构系列❤️《栈(顺序栈与链栈)》——❤️知识点讲解+代码实现