Python数据结构系列☀️《树与二叉树-基础知识》——知识点讲解+代码实现☀️
Posted Vax_Loves_1314
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python数据结构系列☀️《树与二叉树-基础知识》——知识点讲解+代码实现☀️相关的知识,希望对你有一定的参考价值。
数据结构之树和二叉树
第一部分 树和二叉树的基础知识
1、树和二叉树的定义
1.1 树的定义
树(Tree)是n(n≥0)个结点的有限集,它或为空树(n=0);或为非空树,对于非空树T:
- (1)有且仅有一个称之为根的结点;
- (2)除根结点以外的其余结点可分为m(m>0)个互不相交的有限集T₁,T₂,…,Tm,其中每一个结合本身又是一棵树,并且成为根的子树(SubTree)。
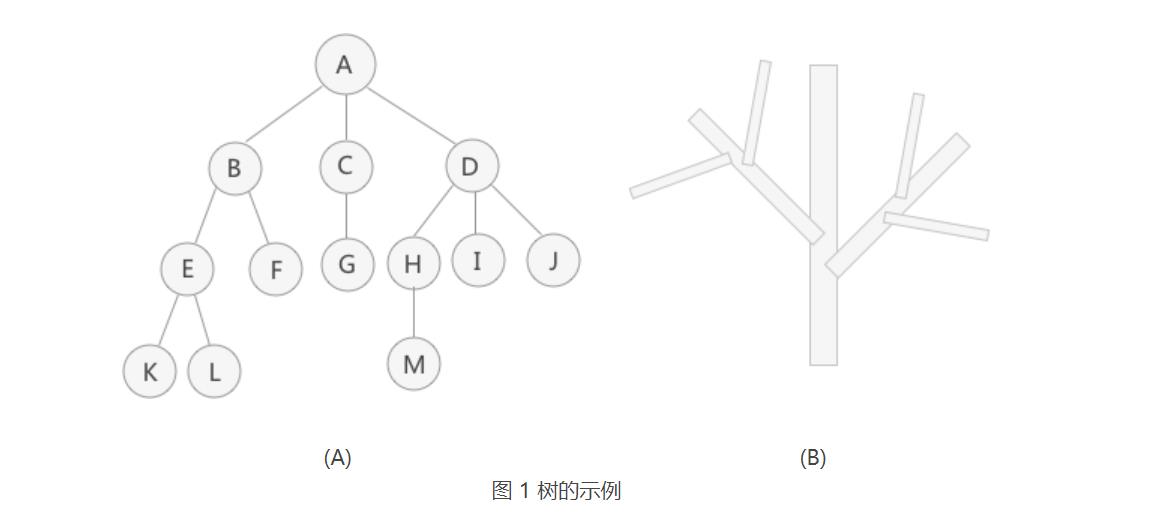
图 1(A) 是使用树结构存储的集合 {A,B,C,D,E,F,G,H,I,J,K,L,M} 的示意图。对于数据 A 来说,和数据 B、C、D 有关系;对于数据 B 来说,和 E、F 有关系。这就是“一对多”的关系。将具有“一对多”关系的集合中的数据元素按照图 1(A)的形式进行存储,整个存储形状在逻辑结构上看,类似于实际生活中倒着的树(图 1(B)倒过来),所以称这种存储结构为“树型”存储结构。
1.2 树的基本术语
(1)结点:树中的一个独立单元。包含一个数据元素及若干指向其子树的分支,如图1(A)中的A、B、C、D等。
(2)结点的度:结点拥有的子树数成为结点的度。例如,A的度为3,C的度为1,F的度为0。
(3)树的度:树的度是树内各结点度的最大值。图1(A)所示的树的度为3。
(4)叶子:度为0的结点称为非终端结点或分支结点。除根节点之外,非终端结点也成为内部结点。
(5)非终端结点:度不为0的结点称为叶子或终端结点。结点K、L、F、G、M、I、J都是树的叶子。
(6)双亲和孩子:结点的子树的根称为该结点的孩子,相应地,该结点称为孩子的双亲。例如,B的双亲为A,B的孩子有E和F。
(7)兄弟:同一个双亲的孩子之间互称兄弟。例如,H、I和J互为兄弟。
(8)祖先:从根到该结点所经分支上的所有结点。例如,M的祖先为A、D和H。
(9)子孙:以某结点为根的子树中的任一结点都称为该结点的子孙。如B的子孙为E、K、L和F。
(10)层次:结点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一结点的层次等于双亲结点的层次加1。
(11)堂兄弟:双亲在同一层的结点互为堂兄弟。例如,结点G与E、F、H、I、J互为堂兄弟。
(12)树的深度:树中结点的最大层次称为树的深度或高度。图1(A)所示的树的深度为4。
(13)有序树和无序树:如果将树中结点的各子树看成从左至右是有次序的(即不能互换),则称该树为有序树,否则称为无序树。在有序树中最左边的子树的根称为第一个孩子,最右边的称为最后一个孩子。
(14)森林:是m(m≥0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。由此,也可以用森林和树互相递归的定义来描述树。
1.3 二叉树的定义
二叉树(Binary Tree)是n(n≥0)个结点所构成的集合,它或为空树(n=0);或为非空树,对于非空树:
(1)有且仅有一个称之为根的结点;
(2)除根结点以外的其余结点分为两个互不相交的子集T₁和T₂,分别称为T的左子树和右子树,且T₁和T₂本身又都是二叉树。
二叉树与树一样具有递归性质,二叉树与树的区别主要有以下两点:
(1)二叉树每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点);
(2)二叉树的子树有左右之分,其次序不能任意颠倒。
二叉树的递归定义表明二叉树或为空,或是由一个根结点加上两棵分别称为左子树和右子树的、互不想交的二叉树组成。由于这两棵子树也是二叉树,则由二叉树的定义,它们也可以是空树。由此,二叉树可以有5种基本形态,如下图所示。
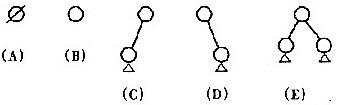
树的基本术语是都适用于二叉树的。
2、二叉树的性质和存储结构
2.1 二叉树的性质
二叉树具有以下几个性质:

二叉树还有两种特殊的形态,满二叉树和完全二叉树。
- 如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。
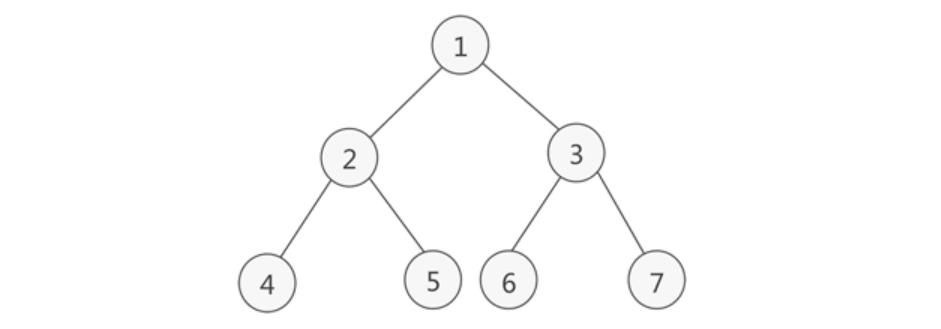
- 如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
2.2 二叉树的存储结构
二叉树的存储结构有两种,分别为顺序存储和链式存储。
2.2.1 顺序存储
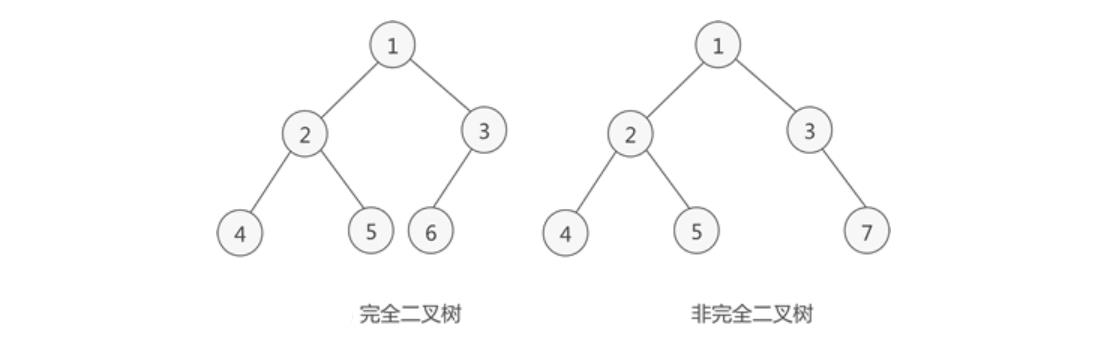
二叉树的顺序存储,指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如下图所示,左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
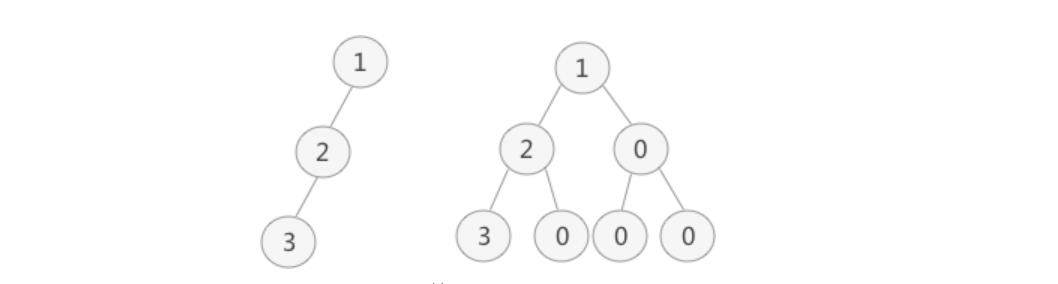
解决了二叉树的转化问题,接下来我们来学习如何顺序存储完全(满)二叉树。完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。
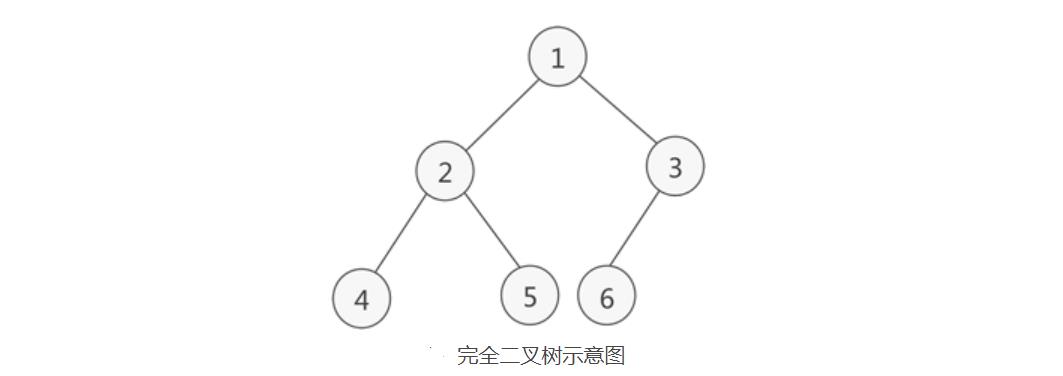
例如,存储上图所示的完全二叉树,其存储状态如下图所示:

由此,我们就实现了完全二叉树的顺序存储。
2.2.2 链式存储
其实二叉树并不合适用数组存储,因为并不是每个二叉树都是完全二叉树,普通二叉树使用顺序表存储会存在空间浪费的现象。接下来介绍二叉树的链式存储结构。
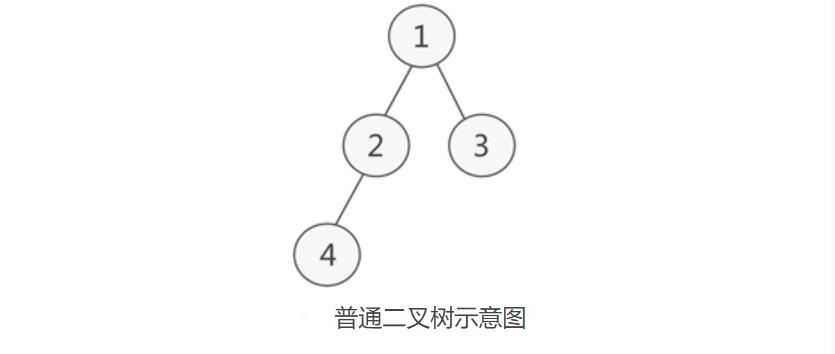
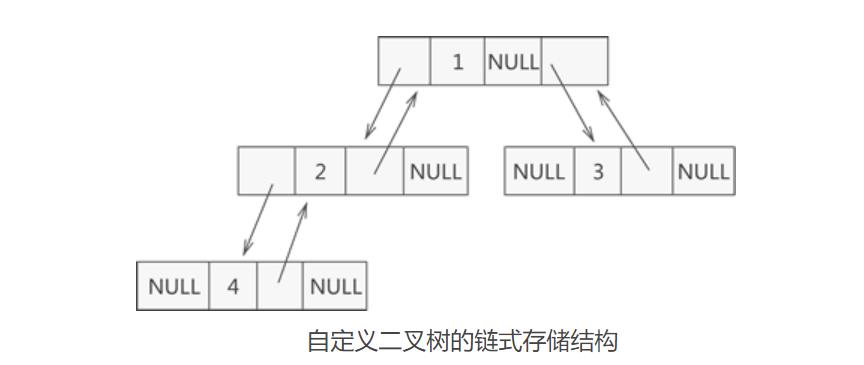
上图为一颗普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。因此,其对应的链式存储结构如下图所示:
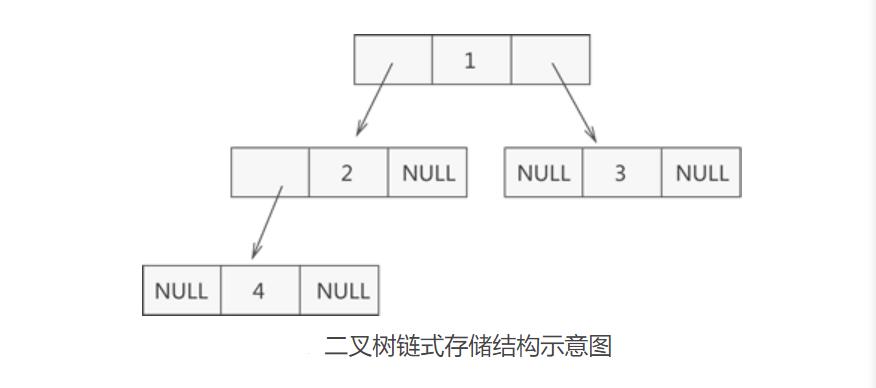
由上图可知,采用链式存储二叉树时,其节点结构由 3 部分构成:
- 指向左孩子节点的指针(Lchild);
- 节点存储的数据(data);
- 指向右孩子节点的指针(Rchild);

其实,二叉树的链式存储结构远不止上图 所示的这一种。例如,在某些实际场景中,可能会做 “查找某节点的父节点” 的操作,这时可以在节点结构中再添加一个指针域,用于各个节点指向其父亲节点,如下图 所示:
利用上图所示的三叉链表,我们可以很轻松地找到各节点的父节点。因此,在解决实际问题时,用合适的链表结构存储二叉树,可以起到事半功倍的效果。
2.3 遍历二叉树
在二叉树的一些应用中,常常要求在树中查找具有某种特征的结点,或者是对树中的全部结点逐一处理,这就提出了一个遍历二叉树的问题。遍历二叉树(traversing binary tree)是指按某条搜索路径巡访树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。访问的含义很广,可以是对结点做各种处理,包括输出结点的信息,对结点进行运算和修改等。遍历二叉树是二叉树最基本的操作,也是二叉树其他各种操作的基础,遍历的实质是对二叉树进行线性化的过程,即遍历的结果是将非线性结构的树中结点排成一个线性序列。由于二叉树的每个结点都有可能有两棵子树,因而需要寻找一种规律,以便使二叉树上的结点能排列在一个线性队列上,从而便于遍历。
二叉树是有3个基本单元组成:根节点、左子树和右子树。因此,若能依次遍历这三部分,便是遍历了整个二叉树。假如L、D、R分别表示遍历左子树、访问根节点和遍历右子树,则可有DLR、LDR、LRD、DRL、RDL、RLD这6种遍历二叉树的方案。若限定先左后右,则只有前3中情况,分别称之为先(根)序遍历、中(根)序遍历和后(根)序遍历。
基于二叉树的递归定义,可得下述遍历二叉树的递归算法定义。
先序遍历二叉树的操作定义如下:
若二叉树为空,则空操作;否则
(1)访问根节点;
(2)先序遍历左子树;
(3)先序遍历右子树。
中序遍历二叉树操作定义如下:
若二叉树为空,则空操作;否则
(1)中序遍历左子树;
(2)访问根节点;
(3)中序遍历右子树。
后序遍历二叉树的操作定义如下:
若二叉树为空,则空操作;否则
(1)后序遍历左子树;
(2)后序遍历右子树;
(3)访问根节点。
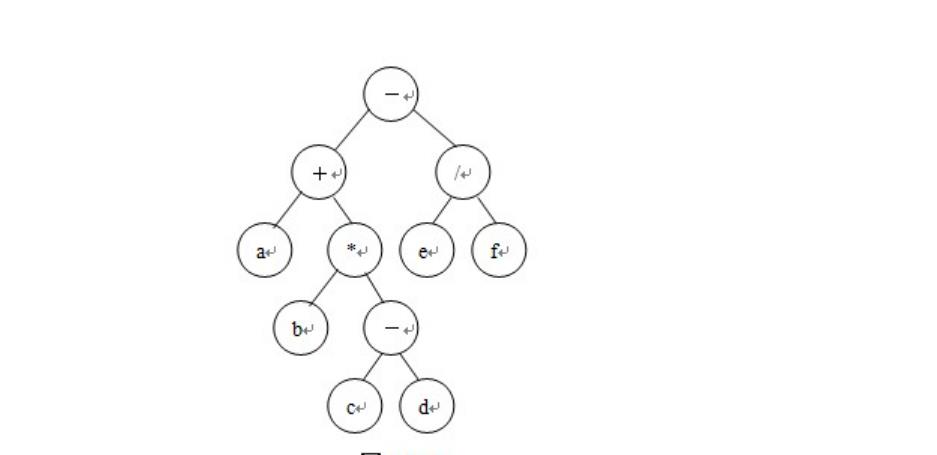
例如,上图的二叉树表示的为表达式:a+b*(c-d)-e/f
- 若先序遍历此二叉树,可得到二叉树的先序序列为:-+a*b-cd/ef
- 类似地,中序遍历此二叉树,可得此二叉树的中序序列为:a+b*c-d-e/f
- 后序遍历此二叉树,可得此二叉树的后序序列为:abcd-*+ef/-
大作业一:二叉树的基本操作
构建二叉树(遍历列表按照先序顺序插入二叉树中的值),用Python编程完成,并完成以下操作:(包括但不限于,可以根据自己能力继续扩展)
- 递归前序遍历二叉树
- 非递归前序遍历二叉树
- 递归中序遍历二叉树
- 非递归中序遍历二叉树
- 递归后序二叉树
- 非递归遍历二叉树
- 返回二叉树的深度
- 返回二叉树的结点数目
- 复制二叉树
最后输出结果要求:
测试案例的输入列表为[‘A’,‘B’,‘C’,’#’,’#’,‘D’,‘E’,’#’,‘G’,’#’,’#’,‘F’,’#’,’#’,’#’],输出的遍历结果见下图。
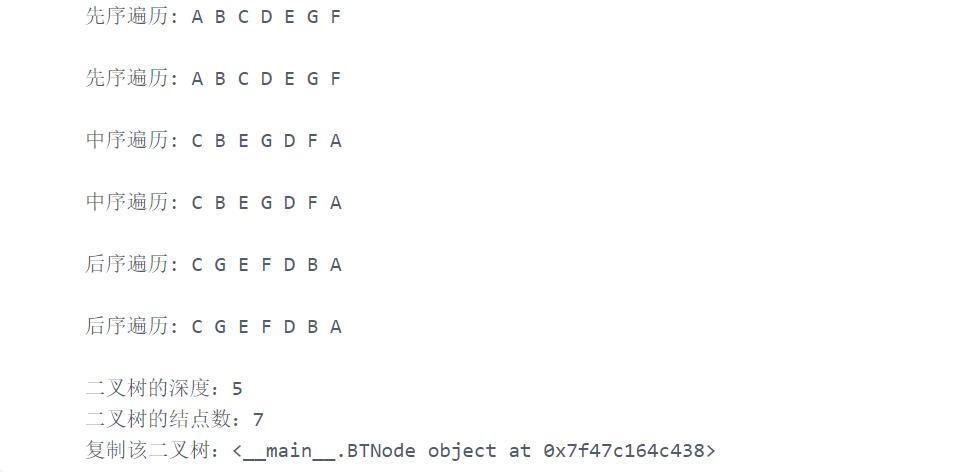
【注】:二叉树的生成,需要用以上输入列表的数值哦;对于非递归遍历,需要用到栈。
代码思路(仅供参考,思路不限):
二叉树的生成:
1、构建结点类,构建二叉树类
2、输入一个列表,然后从列表中取数,按照先序顺序进行递归插入数值,即先创建根结点,再左子树,再右子树。
3、首先输入一个字符,判断其是否为#,不是#的即创建根结点,该结点的数值域为该字符,继续递归生成左子树, 输入第二个字符,判断其是否为#,不是#的即生成结点,是#的将返回上一层递归,如此判断递归生成二叉树。
二叉树的遍历:按照先序、中序、后序遍历的顺序输出字符即可,主要是非递归的遍历是需要借助栈的,拿中序遍历的非递归算法思想来举例:定义一个空栈,从根结点开始访问,若当前节点非空,则将该节点压栈并访问其左子树,循环执行,直至当前节点为空时,取栈顶元素访问并弹栈,然后访问其右子树,再重复如上操作,直至遍历节点的指针为空在且栈也为空。
代码(递归写法):
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2021/8/18 8:16
# @Author : vaxtiandao
# @File : Binary tree.py
class Tree():
def __init__(self, item):
self.item = item
self.l = None
self.r = None
def llink(self, other): # 左连接子节点
self.l = other
def rlink(self, other): # 右连接子节点
self.r = other
# def __repr__(self):
# return str(self.item)+' '+str(self.l)+' '+str(self.r)
def get_depth(self): # 获取深度(递归)
if self.l == None:
l_depth = 0
else:
l_depth = self.l.get_depth()
if self.r == None:
r_depth = 0
else:
r_depth = self.r.get_depth()
return max(l_depth, r_depth) + 1
def get_len(self): # 获取节点数(递归)
if self.l == None:
l_len = 0
else:
l_len = self.l.get_len()
if self.r == None:
r_len = 0
else:
r_len = self.r.get_len()
return l_len + r_len + 1
def show_first(self): # 先序遍历(递归)
print(self.item, end=' ')
if self.l != None:
self.l.show_first()
if self.r != None:
self.r.show_first()
def show_mid(self): # 中序遍历(递归)
if self.l != None:
self.l.show_mid()
print(self.item, end=' ')
if self.r != None:
self.r.show_mid()
def show_last(self): # 后序遍历(递归)
if self.l != None:
self.l.show_last()
if self.r != None:
self.r.show_last()
print(self.item, end=' ')
def copy(self): # 拷贝节点
c_result = Tree(self.item)
c_result.llink(self.l)
c_result.rlink(self.r)
return c_result
def copy_deep(self): # 深拷贝节点以下整个树
c_result = Tree(self.item)
if self.l != None:
c_result.llink(self.l.copy())
if self.r != None:
c_result.rlink(self.r.copy())
return c_result
def create(x): # 根据列表创建二叉树
try:
tmp = next(x)
if tmp == '#':
return
root = Tree(tmp)
root.llink(create(x))
root.rlink(create(x))
return root
except:
pass
tree_list = ['A', 'B', 'C', '#', '#', 'D', 'E', '#', 'G', '#', '#', 'F', '#', '#', '#']
it = iter(tree_list)
root = create(it)
# 先序遍历
print(root.show_first())
# 中序遍历
print(root.show_mid())
# 后序遍历
print(root.show_last())
实现效果:

代码(非递归,借用栈):
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2021/8/18 8:43
# @Author : vaxtiandao
# @File : Binary tree2.py
# 定义结点类,包含两个成员:结点元素值和指向下一结点的指针
class SingleNode():
# 结点类初始化
def __init__(self, item):
self.item = item # item存放结点的数值
self.next = None # 下一指针指向
# 定义链栈
class LinkStack():
# 初始化
def __init__(self):
self.top = None
# 判断是否为空
def is_empty(self):
if self.top == None:
return True
else:
return False
# 返回栈顶元素
def get_element(self):
if self.is_empty():
return None
else:
return self.top.item
# 返回栈长度
def get_length(self):
tmp = self.top
if tmp == None:
return 0
i = 0
while tmp != None:
tmp = tmp.next
i += 1
return i
# 进栈
def add_stack(self, element):
node = SingleNode(element)
node.next = self.top # 指针变换
self.top = node
# 出栈
def remove_stack(self):
if self.is_empty():
raise IndexError("栈已空,无法出栈")
else:
node = self.top
self.top = self.top.next
return node.item
# 清空栈
def clear_stack(self):
self.top = None
class Tree():
def __init__(self,item):
self.item=item
self.l=None
self.r=None
def llink(self,other): #左连接子节点
self.l=other
def rlink(self,other): #右连接子节点
self.r=other
# def __repr__(self):
# return str(self.item)+' '+str(self.l)+' '+str(self.r)
def get_depth(self): #获取深度(递归)
if self.l==None:
l_depth=0
else:
l_depth=self.l.get_depth()
if self.r==None:
r_depth=0
else:
r_depth=self.r.get_depth()
return max(l_depth,r_depth)+1
def get_len(self): #获取节点数(递归)
if self.l==None:
l_len=0
else:
l_len=self.l.get_len()
if self.r==None:
r_len=0
else:
r_len=self.r.get_len()
return l_len+r_len+1
def show_first(self): #先序遍历(递归)
print(self.item,end=' ')
if self.l !=None:
self.l.show_first()
if self.r !=None:
self.r.show_first()
def show_mid(self): #中序遍历(递归)
if self.l !=None:
self.l.show_mid()
print(self.item,end=' ')
if self.r !=None:
self.r.show_mid()
def show_last(self): #后序遍历(递归)
if self.l !=None:
self.l.show_last()
if self.r !=None:
self.r.show_last()
print(self.item,end=' ')
def copy(self): #拷贝节点
c_result=Tree(self.item)
c_result.llink(self.l)
c_result.rlink(self.r)
return c_result
def copy_deep(self): #深拷贝节点以下整个树
c_result=Tree(self.item)
if self.l!=None:
c_result.llink(self.l.copy())
if self.r!=None:
c_result.rlink(self.r.copy())
return c_result
def create(x): #根据列表创建二叉树
try:
tmp=next(x)
if tmp=='#':
return
root=Tree(tmp)
root.llink(create(x))
root.rlink(create(x))
return root
except:
pass
def show_first(tree): # 非递归先序遍历(利用栈)
if tree == None: # 如果树为空,返回空
return None
stack = LinkStack() # 如果树不为空,利用栈遍历
tmp = tree # tmp指针指向根节点
stack.add_stack(tmp) # 根节点入栈
while not stack.is_empty(): # 当栈不为空时,不断出栈
tmp = stack.remove_stack()
print(tmp.item, end=' ') # 访问并打印当前节点内容
if tmp.r != None: # 将当前节点的子节点入栈(为了保证先访问左树,先入栈右节点)
stack.add_stack(tmp.r)
if tmp.l != None:
stack.add_stack(tmp.l)
def show_mid(tree): # 非递归中序遍历
if tree == None:
return None
stack = LinkStack()
tmp = tree # 定义指针
while tmp != None or (not stack.is_empty()): # 指针不为空或栈不为空
while tmp != None: # 将当前节点入栈,并查找左树的最左端
stack.add_stack(tmp)
tmp = tmp.l
if not stack.is_empty(): # 找到左树最左端后,出栈一个节点,此节点为最左端节点
tmp = stack.remove_stack()
print(tmp.item, end=' ') # 访问当前节点
tmp = tmp.r # 指针指向右节点
def show_last(tree): # 非递归后序遍历(利用2个栈,用逆先序DRL访问整个树后,利用第二个栈将结果保存并反转,即可得到后序LRD访问的结果)
if tree == None:
return None
stack = LinkStack()
out_stack = LinkStack()
tmp = tree
stack.add_stack(tmp)
while not stack.is_empty():
tmp = stack.remove_stack()
out_stack.add_stack(tmp) # 访问节点并入栈结果保存的栈
if tmp.l != None:
stack.add_stack(tmp.l) # 其他部分与先序类似,但左右子节点入栈顺序需反转
if tmp.r != None:
stack.add_stack(tmp.r)
while not out_stack.is_empty(): # 将结果出栈,达到反转顺序效果
print(out_stack.remove_stack().item