人工智能数学基础--不定积分1：概念与性质

Posted 2021-08-20 LaoYuanPython

一、引言

导数运算是根据一个函数求该函数对应导数的运算，导数本质上反映了函数在函数某点的运动态势，而不定积分则是根据一个已知的导函数求原函数，因此二者可以说是逆运算。

二、定义

2.1、 原函数定义

如果在区间I上，可导函数F(x)的导函数为(x)，即对任一x∈I，都有：

F’(x)=f(x) 或 dF(x)=f(x)dx，

那么函数F(x)就称为f(x)(或f(x)dx)在区间I上的一个原函数。

2.2、原函数存在定理

定理：如果函数f(x)在区间I上连续，那么在区间I上存在可导函数F(x)，使对任一x∈I都有：

F’(x)=f(x)。

简单地说就是：连续函数一定有原函数。

2.3、不定积分定义

如果f(x)在区间I上有原函数，即有一个函数F(x)，使对任一x∈I，都有F’(x)=f(x)，那么，对任何常数C，显然也有：

[F(x)+C]’=f(x)

即对任何常数C，函数F(x)+C也是f(x)的原函数**。这说明**，如果f(x)有一个原函数，那么f(x)就有无限多个原函数。

定义：
在区间I上，函数f(x)的带有任意常数项的原函数称为f(x)(或f(x)dx)在区间I上的不定积分，记作:

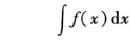
其中记号 ∫ 称为积分号，f(x)称为被积函数，f(x)dx称为被积表达式，x称为积
分变量。

由此定义及前面的说明可知，如果F(x)是f(x)在区间I上的一个原函数，那么F(x)+C就是f(x)的不定积分，即：∫ f(x)dx=F(x)+C

因而不定积分∫ f(x)dx可以表示f(x)的任意一个原函数。

函数f(x)对应的原函数几何图形称为f(x)的积分曲线。

由不定积分的定义可知：不定积分∫ f(x)dx是f(x)的原函数，所以：

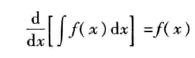
或：

d[∫f(x)dx] = f(x)dx

d[∫F’(x)dx]=∫dF(x)=F(x)+C

由此可见，微分运算（以记号d表示）与求不定积分的运算是互逆的，当记号d与∫连在一起时，要么相互抵消，要么抵消后差一个常数。

三、基本积分表

从导数运算可以推导出积分运算，以下十三个基本积分公式是不定积分的基础，必须熟记：

另外针对双曲函数（请参考《人工智能数学基础11：集合、函数及相关概念补充》）有如下积分公式：

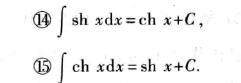
下面是在基本积分公式基础上扩展出来的几个常用公式：

四、不定积分的性质

1. 性质1：如果两个函数的不定积分都存在，则两个函数和的不定积分等于各自不定积分的和，即：
   
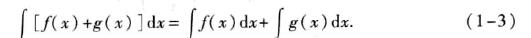
2. 性质2： 函数与常数的乘积的不定积分等于常数与函数不定积分的乘积，即：
   

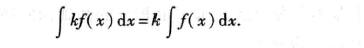
五、小结

本文介绍了不定积分的概念、性质以及基本的不定积分表，需要注意不定积分的运算公式只有加法和数乘的，没有象导数和微分那样还有乘除等运算公式。

说明：

本文内容是老猿学习同济版高数的总结，有需要原教材电子版以及OpenCV、Python基础知识、、图像处理原理介绍相关电子资料，或对文章内有有疑问咨询的，请扫博客首页左边二维码加微信公号，根据加微信公号后的自动回复操作。

更多人工智能数学基础请参考专栏《人工智能数学基础》。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

关于老猿的付费专栏

1. 付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》；
2. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》；
3. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录 》
4. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容，包括爬虫入门的基础知识，以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

老猿Python，跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░