人工智能之数学基础篇—微积分
Posted Roar冷颜
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了人工智能之数学基础篇—微积分相关的知识，希望对你有一定的参考价值。
人工智能之数学基础篇—微积分
微积分作为初等数学和高等数学的分水岭，在现代科学中有着极其重要的作用。17世纪末 ，微积分的概念和技巧不断扩展并被广泛应用于解决天文学、物理学中的各种实际问题。例如，求瞬时速度 、 曲线切线 、 曲线长 、曲线围成的面积 、 由面围成的体积等问题 。
微积分是高等数学中研究函数的微分、积分及有关概念和应用的数学分支 ， 是数学的一个基础学科，内容包括极限 、 微分学、积分学及其应用 。微分学包括导数运算，是一套关于变化率的理论，在人工智能之数学基础篇—高等数学基础中篇中已经介绍过；积分学包括积分运算，为计算面积、 体积、 水压力等几何物理问题提供一套通用的方法。 本文将主要介绍微积分的一些核心概念及如何利用Python编程工具来解决定积分相关的问题 。
在介绍微积分理论之前先来看一个小故事，微积分基本定理又称为牛顿—莱布尼茨公式，从名字就可以看出两个人对微积分的创立都做出了很大贡献，但是在到底谁是微积分的创立者这一问题上，二人曾争论不休。莱布尼茨和牛顿曾是好朋友，但因为这件事，莱布尼茨至死没和牛顿和解。那到底是谁创立了微积分呢？后人核实，两人各自独立地创立了微积分，牛顿在研究物理中的运动问题过程中创立了微积分，而莱布尼茨是从几何方面出发也独立发现了微积分，所以又称牛顿—莱布尼茨公式。
1 微积分的基本思想
微积分以研究函数变化规律为目的，主要运用到的数学工具就是微分和积分。
微分是对函数局部变化率的线性描述。微分学的基本思想是“无限细分”和“等效替代”，其几何意义如图1所示。设函数 y = f ( x ) y=f(x) y=f(x)，假设函数上有一点 p p p，当点 p p p 在沿着横坐标 Δ x \\Delta x Δx 移动时，其在纵坐标上的变化范围为 Δ y \\Delta y Δy，如图1(a)所示。特别的，当 p p p 的移动范围足够小时（ lim Δ x → 0 d y = 0 , lim Δ x → 0 d x = 0 \\lim_{\\Delta x\\rightarrow 0}dy=0,\\: \\lim_{\\Delta x\\rightarrow 0}dx=0 limΔx→0dy=0,limΔx→0dx=0，如图1(b)所示）， p p p 点纵坐标的变化值 Δ y \\Delta y Δy 与该点切线的变化距离 d y dy dy 之间的差值 ∣ Δ y − d y ∣ \\left | \\Delta y-dy \\right | ∣Δy−dy∣ 比 Δ y \\Delta y Δy 要小的多，这时可以用 p p p 点附近的一个切线段来近似替代原函数。
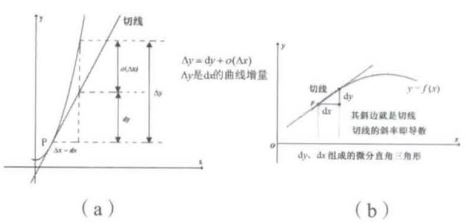
p p p 点切线的斜率是导数，而 f ( x ) ′ = d y d x f\\left ( x \\right )^{'}=\\frac{dy}{dx} f(x)′=dxdy，所以 d y = f ( x ) ′ d x dy = f\\left ( x \\right )^{'}dx dy=f(x)′dx。根据无穷小的概念， d x dx dx， d y dy dy 都是微分。
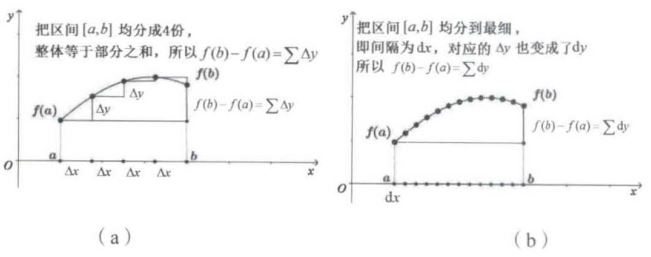
积分是在确定函数的导数基础上通过一定的数学方法对原函数进行求解的过程。积分的基本思想是通过微分的 “无限求和” 来进行的 。 微分是对函数的求导过程，因此可以将积分看作微分的一个逆向过程，其几何意义如图 2 所示。设函数 y = f ( x ) y=f(x) y=f(x) 把区间 [ a a a， b b b] 均分为 4 份，如图2(a)所示 ，整体等于部分之和，即 f ( b ) − f ( a ) = ∑ Δ y f(b)-f(a)=\\sum \\Delta y f(b)−f(a)=∑Δy。继续细分，如图2(b)所示，把区间均分到最细，即间隔为 d x dx dx，对应的 Δ y \\Delta y Δy 也变成了 d y dy dy ， 所以 f ( b ) − f ( a ) = ∑ d y f(b)-f(a)=\\sum dy f(b)−f(a)=∑dy。根据前面微分的无限细分可知 d y = f ( x ) ′ d x dy = f\\left ( x \\right )^{'}dx dy=f(x)′dx，因此 f ( b ) − f ( a ) = ∑ f ( x ) ′ d x f(b)-f(a)=\\sum f\\left ( x \\right )^{'}dx f(b)−f(a)=∑f(x)′dx。
2 微积分的解释
下面来讨论一个问题，如何求解曲边梯形的面积？
设曲线方程为 y = f ( x ) y=f(x) y=f(x)，在区间 [ a a a， b b b] 上非负、连续 。 由直线 x = a x=a x=a ， x = b x=b x=b , y = 0 y=0 y=0 及曲线 y = f ( x ) y =f(x) y=f(x) 所围成的平面图形如图 3 所示，称之为曲边梯形，其中曲线弧段称为曲边梯形的曲边。
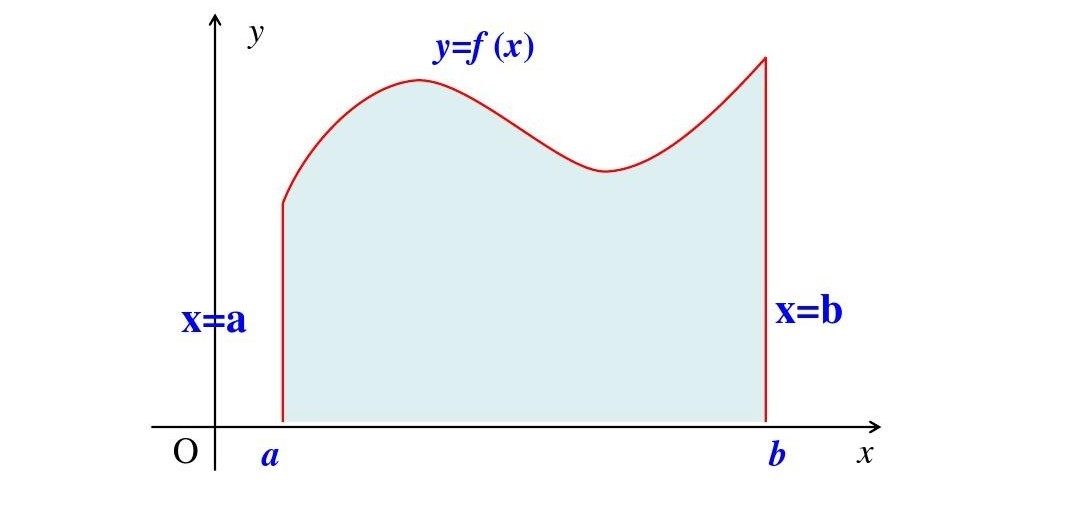
曲边梯形面积不像矩形 、圆等规则图形有特定的公式求解，但可以采用以直代曲的思想来进行求解。
分别以 4 个小矩形和 9 个小矩形替代，如图4所示 。
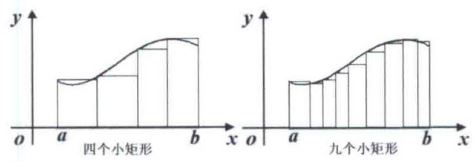
可以看出 9 个小矩形比 4 个小矩形求面积的精确度高，那么如果无限分割呢？在 a a a 与 b b b 之间分割出 n n n 等份， n n n 趋近于无穷，是不是会无限接近曲边梯形的面积呢? 曲边梯形的无限分割如图5所示。
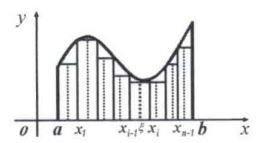
因此，将其极限值
A
=
lim
n
→
∞
∑
i
=
1
n
f
(
ξ
i
)
Δ
x
i
,
x
i
−
1
<
ξ
i
<
x
i
A=\\lim_{n\\rightarrow \\infty }\\sum_{i=1}^{n}f\\left ( \\xi _{i} \\right )\\Delta x_{i},\\: x_{i-1}< \\xi _{i} < x_{i}
A=n→∞limi=1∑nf(ξi)Δxi,xi−1<ξi<xi定义为曲边梯形的面积。
积分的基本思想就是“无限求和”，需要尽可能地将每一个矩形的底边分割成无穷小，这样所求的结果即为曲边梯形的面积。数学家莱布尼茨为了体现求和的感觉，将 Sum 中的第一个字母 s 拉长了，简写成
S
u
m
[
f
(
x
)
Δ
x
]
⇒
∫
u
m
f
(
x
)
d
x
Sum\\left [ f(x)\\Delta x \\right ]\\Rightarrow \\int_{um}^{}f(x)dx
Sum[f(x)Δx]⇒∫umf(x)dx就成了常见的积分符号
∫
\\int
∫。
下面再来讨论一个问题：求变速直线运动的路程。
设某物体做直线运动，已知速度 ν = ν ( t ) ν=ν(t) ν=ν(t) 是时间间隔 [ t 1 , t 2 t_{1}, t_{2} t1,t2] 上 t t t 的连续函数，且 v ( t ) ⩾ 0 v(t)\\geqslant0 v(t)⩾0，计算在这段时间内物体所经过的路程。
匀速直线运动的公式：路程=速度 x 时间。但是在我们的问题中，速度不是常数，而是随时间变化的变量，因此所求路程 s 不能直接按匀速直线运动的路程公式来计算。物体运动的速度函数
ν
=
ν
(
t
)
ν=ν(t)
ν=ν(t) 是连续变化的，在很短的时间内，速度的变化很小，因此如果把时间间隔分小，在小段时间内，以匀速运动近似代替变速运动，就可以算出各部分路程的近似值，再求和得到整个路程的近似值，最后，通过对时间间隔无限细分的极限过程，求得物体在时间间隔 [
t
1
,
t
2
t_{1}, t_{2}
t1,t2] 内的路程结果如下。
s
=
lim
n
→
∞
∑
i
=
1
n
v
(
ξ
i
)
Δ
t
i
,
t
i
−
1
<
ξ
i
<
t
i
s=\\lim_{n\\rightarrow \\infty }\\sum_{i=1}^{n}v\\left ( \\xi _{i} \\right )\\Delta t_{i},\\: t_{i-1}< \\xi _{i} < t_{i}
s=n→∞limi=1∑以上是关于人工智能之数学基础篇—微积分的主要内容，如果未能解决你的问题，请参考以下文章
干货来袭！3天0基础Python实战项目快速学会人工智能必学数学基础全套（含源码）（第3天）概率分析篇：条件概率全概率与贝叶斯公式