1074. 元素和为目标值的子矩阵数量（二维前缀和）

Posted 2021-08-18 mp-ui

1074. 元素和为目标值的子矩阵数量

题目描述

给出矩阵 matrix 和目标值 target，返回元素总和等于目标值的非空子矩阵的数量。

子矩阵 x1, y1, x2, y2 是满足 x1 <= x <= x2 且 y1 <= y <= y2 的所有单元 matrix[x][y] 的集合。

如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 两个子矩阵中部分坐标不同（如：x1 != x1'），那么这两个子矩阵也不同。

示例 1：

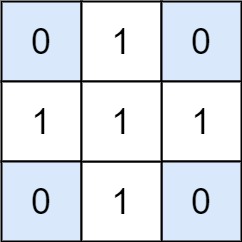
输入：matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
输出：4
解释：四个只含 0 的 1x1 子矩阵。

示例 2：

输入：matrix = [[1,-1],[-1,1]], target = 0
输出：5
解释：两个 1x2 子矩阵，加上两个 2x1 子矩阵，再加上一个 2x2 子矩阵。

示例 3：

输入：matrix = [[904]], target = 0
输出：0

提示：

• 1 <= matrix.length <= 100
• 1 <= matrix[0].length <= 100
• -1000 <= matrix[i] <= 1000
• -10^8 <= target <= 10^8

通过次数8,365

提交次数13,615

解法1：二维前缀和

通过题目很容易可以发现，这道题可以通过二维前缀和来做，时间复杂度O(n^4)

class Solution {
    public int numSubmatrixSumTarget(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] pre = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                pre[i][j] = pre[i][j - 1] + pre[i - 1][j] - pre[i - 1][j - 1] + matrix[i - 1][j - 1];
            }
        }
        int ans = 0;
        for (int i1 = 1; i1 <= m; i1++) {
            for (int j1 = 1; j1 <= n; j1++) {
                for (int i2 = i1; i2 <= m; i2++) {
                    for (int j2 = j1; j2 <= n; j2++) {
                        if (pre[i2][j2] - pre[i2][j1-1] - pre[i1-1][j2] + pre[i1-1][j1-1] == target) {
                            ++ans;
                        }
                    }
                }
            }
        }
        return ans;
    }
}

运行结果：

相似题目：304. 二维区域和检索 - 矩阵不可变