⭐算法入门⭐《动态规划 - 线性DP》中等01 —— LeetCode 198. 打家劫舍

Posted 2021-08-16 英雄哪里出来

🙉饭不食，水不饮，题必须刷🙉
还不会C语言，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？上简单题！ 🧡《C语言入门100例》🧡
LeetCode 太简单？大神盘他！ 🌌《夜深人静写算法》🌌

文章目录

• 一、题目
• • 1、题目描述
  • 2、基础框架
  • 3、原题链接
• 二、解题报告
• • 1、思路分析
  • 2、时间复杂度
  • 3、代码详解
• 三、本题小知识

一、题目

1、题目描述

  作为一个专业大盗，要开始执行偷窃任务。房屋按照线性排列，每间房内都藏有一定的现金，影响偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会报警。给定一个代表每个房屋存放金额的非负整数数组，计算 不触动警报装置 的情况下 ，一夜之内能够偷窃到的最高金额。
  样例输入： $[2,7,19,3,1]$
  样例输出： $22$

2、基础框架

• c++ 版本给出的基础框架代码如下：

class Solution {
public:
    int rob(vector<int>& nums) {
    }
};

3、原题链接

LeetCode 198. 打家劫舍

二、解题报告

1、思路分析

比较直观的思路就是：如果第 $i$ 个房间被偷窃，那么第 $i-1$ 个房间一定不能被偷窃。

• 令第 $i$ 个房间被偷窃时，前 $i$ 个房间的最大偷窃金额为 $f[i]$。
• 则因为偷窃房间不能相邻，所以上一个被偷窃的房间一定是 $0$ 到 $i-2$。
• 所以对于每个被偷窃的房间 $i$，枚举上一个被偷窃的房间 $j(j\in [0,i-2])$。就能够计算出所有的情况，取最大值就是我们要的解，状态转移方程如下：
• $$\begin{gathered} f[i]=\max (f[j]+nums[i]) \\ (0\le j<i-1) \end{gathered}$$
  

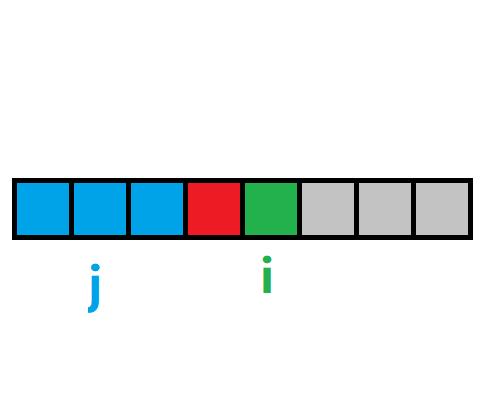
如图所示：
  绿色格子 代表当前要计算的状态；
  红色格子 代表不能进行状态转移的状态；
  蓝色格子 代表能够转移到绿色格子的状态；
  灰色格子 则代表尚未计算出来的状态。

• 最后，$\max (f[i])$ 就是我们要求的答案。

2、时间复杂度

• 状态数：$O(n)$
• 状态转移：$O(n)$
• 时间复杂度：$O(n^2)$

3、代码详解

class Solution {
    int f[110];
public:
    int rob(vector<int>& nums) {
        f[0] = nums[0];                            
        int ans = f[0];                             // (1)
        for(int i = 1; i < nums.size(); ++i) {
            f[i] = nums[i];                         // (2)
            for(int j = 0; j < i - 1; ++j) {
                f[i] = max(f[i], nums[i] + f[j]);   // (3)
            } 
            ans = max(f[i], ans);                   // (4)
        }
        return ans;
    }
};

• $(1)$ 代表第 0 个房间进行偷窃的最大现金；
• $(2)$ 这种情况代表第 $i$ 个房间进行偷窃，并且前面 $i-1$ 个都不进行偷窃的情况；
• $(3)$ 根据策略执行状态转移；
• $(4)$ 每次取第 $i$ 个房间作为最后一个偷窃房间所得到的的最大现金作为候选值，取最大值就是最后的答案；

---

三、本题小知识

动态规划的时间复杂度 = 状态数 $\times$ 状态转移的时间复杂度。

---