ACM - 动态规划小白入门：背包 / 线性 / 区间 / 计数 / 数位统计 / 状压 / 树形 / 记忆化 DP

Posted 2021-08-17 肆呀

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了ACM - 动态规划小白入门：背包 / 线性 / 区间 / 计数 / 数位统计 / 状压 / 树形 / 记忆化 DP相关的知识，希望对你有一定的参考价值。

动态规划 - AcWing 基础课

一、背包问题
二、线性 DP
三、区间DP
- AcWing 282. 石子合并
四、计数类DP
- AcWing 900. 整数划分
五、数位统计DP
- AcWing 338. 计数问题
六、状态压缩DP
- AcWing 291. 蒙德里安的梦想
- AcWing 91. 最短Hamilton路径
七、树形DP
- AcWing 285. 没有上司的舞会
八、记忆化搜索
- AcWing 901. 滑雪

【本文主要来自对AcWing基础算法课的整理，基本是母题】

一、背包问题

1、01背包：每件物品最多只能选一次

AcWing 2. 01背包问题

原题链接：https://www.acwing.com/problem/content/2/
在这里插入图片描述
思路

#include <bits/stdc++.h> 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 1010; 
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};

int v[N], w[N];
int dp[N];  //优化空间

int main() {
	//freopen("D:\\\\in.txt", "r", stdin); 
	rin;
	rim;
	for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
	for (int i = 1; i <= n; ++ i) {
		for (int j = m; j >= v[i]; -- j) {
			dp[j] = dp[j];
			dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
		}
	}
	cout << dp[m];
	return 0;
}

2、完全背包 : 每件物品可以选任意次

AcWing 3. 完全背包问题
原题链接：https://www.acwing.com/problem/content/3/
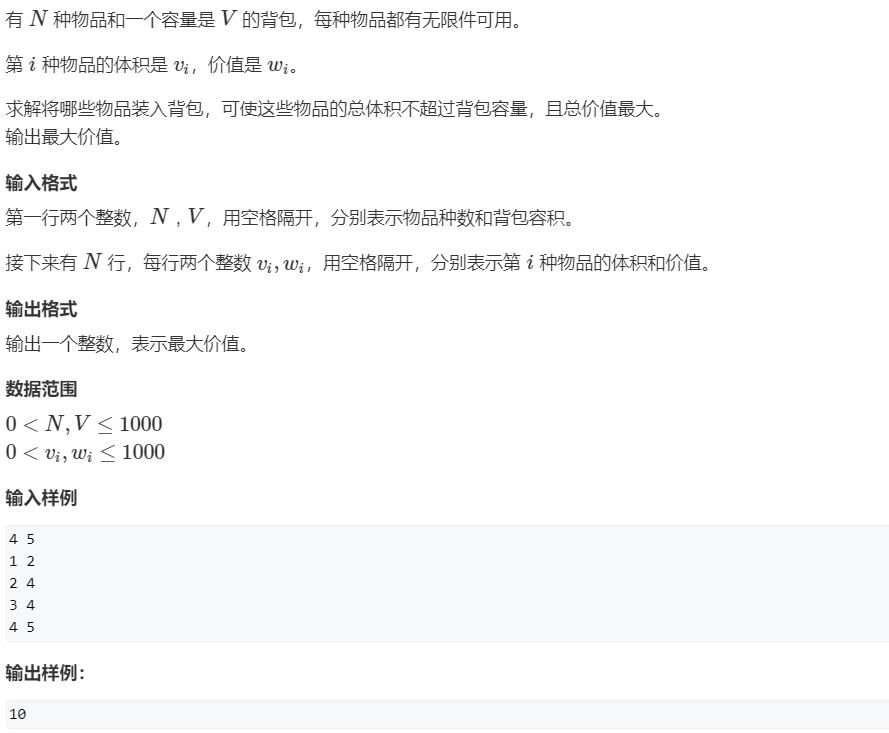
在这里插入图片描述

思路

因为背包的体积不是无限大，所以设每一件物品最多只能放 k 件进背包。
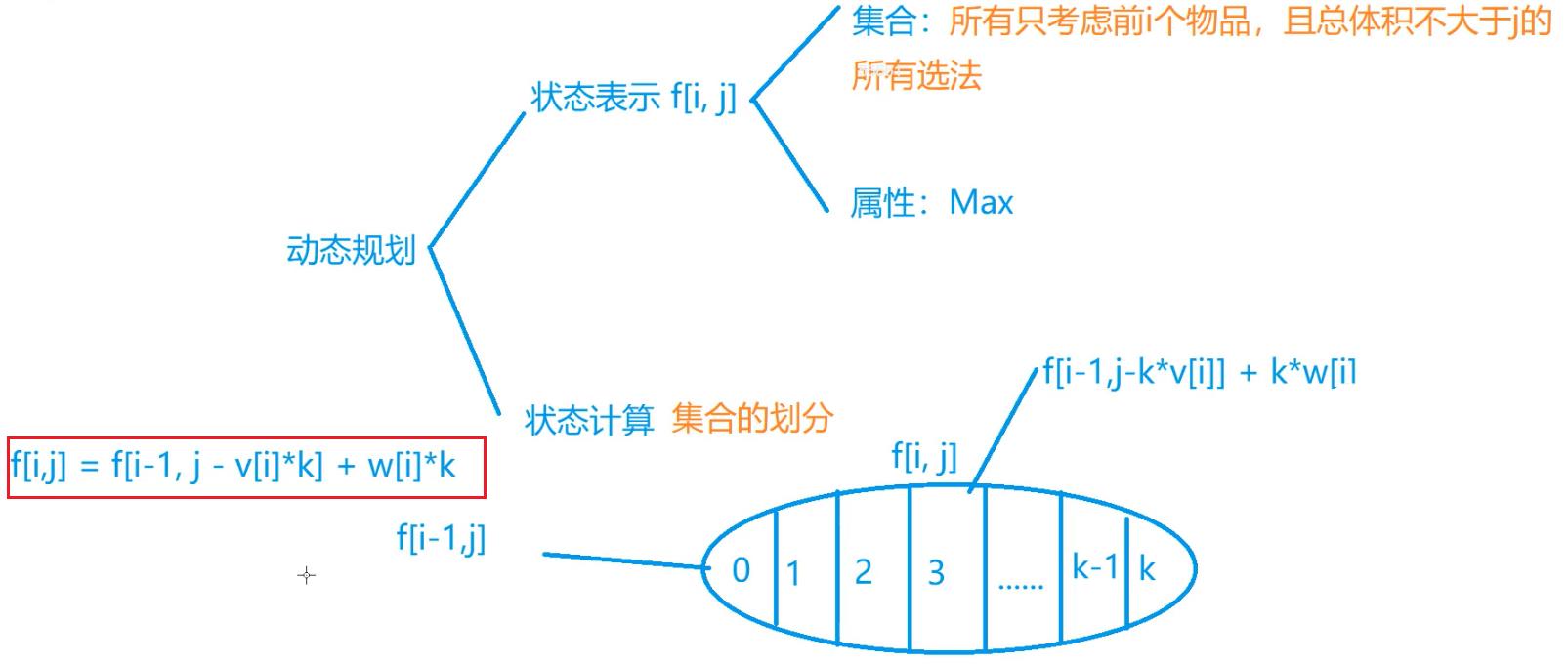
在这里插入图片描述
如果 k 较大，可能会TLE，所以还可以再优化一下：

#include <bits/stdc++.h> 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 1010; 
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};

int v[N], w[N];
int dp[N][N];

int main() {
	//freopen("D:\\\\in.txt", "r", stdin); 
	rin;
	rim;
	for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
	for (int i = 1; i <= n; ++ i) {
		for (int j = 1; j <= m; ++ j) {
			dp[i][j] = dp[i - 1][j];
			if (v[i] <= j) dp[i][j] = max(dp[i][j], dp[i][j - v[i]] + w[i]);
		}
	}
	cout << dp[n][m];
	return 0;
}

3、多重背包（朴素版）：限定每件物品选择次数的上限

AcWing 4. 多重背包问题 I

原题链接：https://www.acwing.com/problem/content/4/
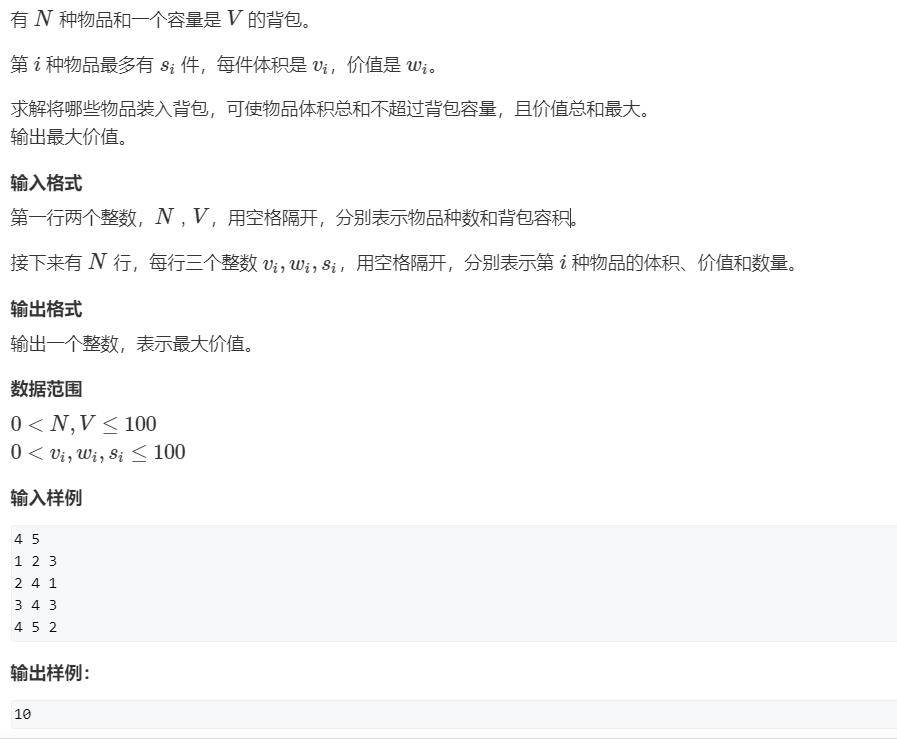
在这里插入图片描述

思路

由于 dp[ i ] [ j - v] 展开后会多出额外的一项（因为有上限 s[ i ]），所以不能和完全背包一样用以前的状态替换掉。
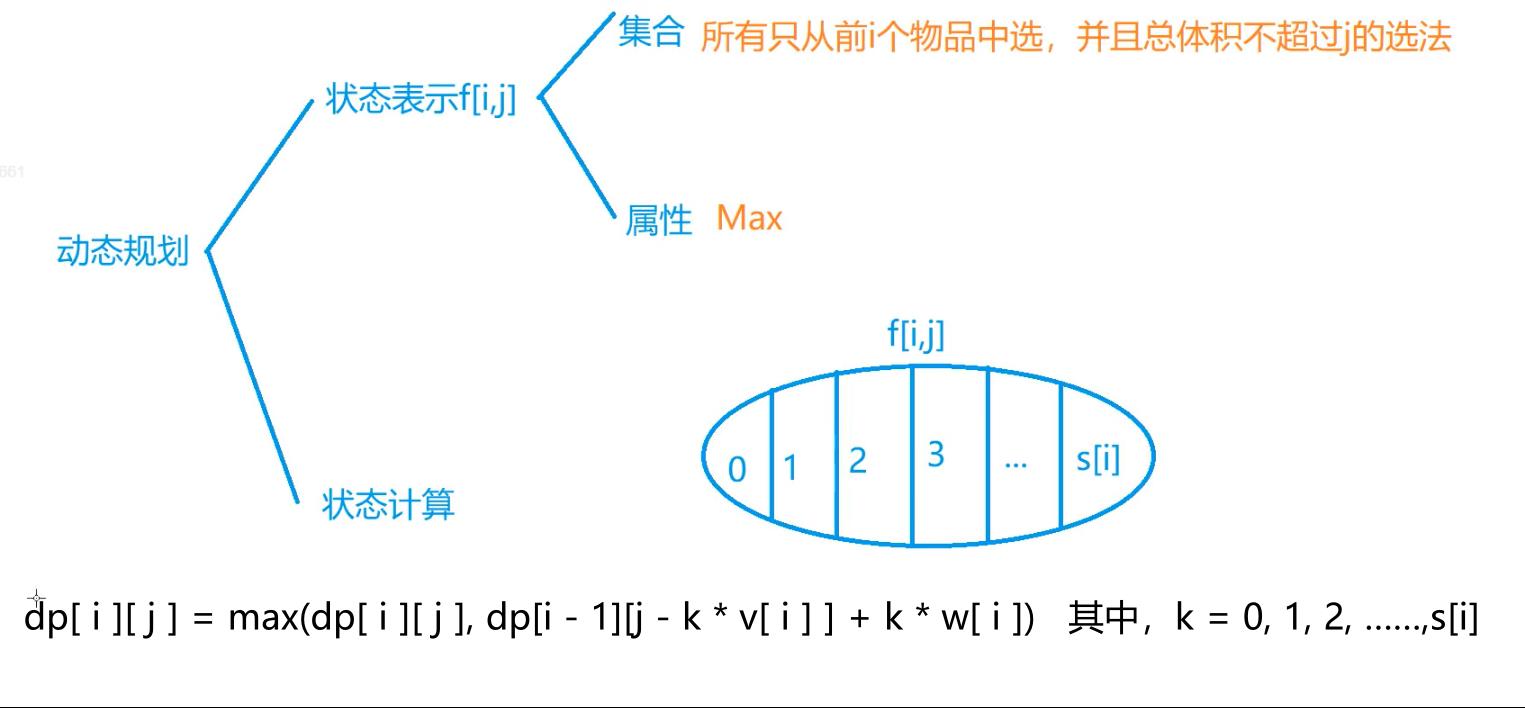
在这里插入图片描述

#include <bits/stdc++.h> 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 110; 
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};

int v[N], w[N], s[N];
int dp[N][N];

int main() {
	//freopen("D:\\\\in.txt", "r", stdin); 
	rin;
	rim;
	for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
	for (int i = 1; i <= n; ++ i) {
		for (int j = 1; j <= m; ++ j) {
			for (int k = 0; k <= s[i] && k * v[i] <= j; ++ k) {
				dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
			}
			
		}
	}
	cout << dp[n][m];
	return 0;
}

4、多重背包（二进制优化版）：限定每件物品选择次数的上限，但是上限较大

AcWing 5. 多重背包问题 II

原题链接：https://www.acwing.com/problem/content/5/
在这里插入图片描述
思路

首先明确一点，用1、2、4、8、……、64 等数可以拼凑起 0 到 127 之间的任意一个数，假如想要拼凑 0 到 200 之间的任意一个数，那么至少需要 1、2、4、8、……、64、73 这些数。

因为题目中 s [ i ] 的范围较大，不可能再开一重循环，所以就考虑将 s [ i ] 拆开为 1、2、4、……，由此可以保证每一种组合都会被涉及到。

最后合成的全新的 v 和 w 数组，再用一次 01 背包即可求得最终解。

#include <bits/stdc++.h> 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 30000; 
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};

int v[N], w[N];
int dp[N];

int main() {
	//freopen("D:\\\\in.txt", "r", stdin); 
	int n, m;
	cin >> n >> m;
	int cnt = 1;
	
	for (int i = 0; i < n; ++ i) {
		int a, b, c;
		cin >> a >> b >> c;
		int num = 1;  // num ：1、2、4、8、……
		while (num <= c) {
			v[cnt] = num * a;
			w[cnt] = num * b;
			++ cnt;
			c -= num;
			num *= 2;
		}
		if (c > 0) {
			v[cnt] = c * a;
			w[cnt] = c * b;
			++ cnt;
		}
	}
	for (int i = 1; i < cnt; ++ i) {
		for (int j = m; j >= v[i]; -- j) {	
			 dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
		}
	}
	cout << dp[m];
	return 0;
}

5、分组背包：分为 x 组，每一组最多只能选择其中的一件

AcWing 9. 分组背包问题

原题链接：https://www.acwing.com/problem/content/9/
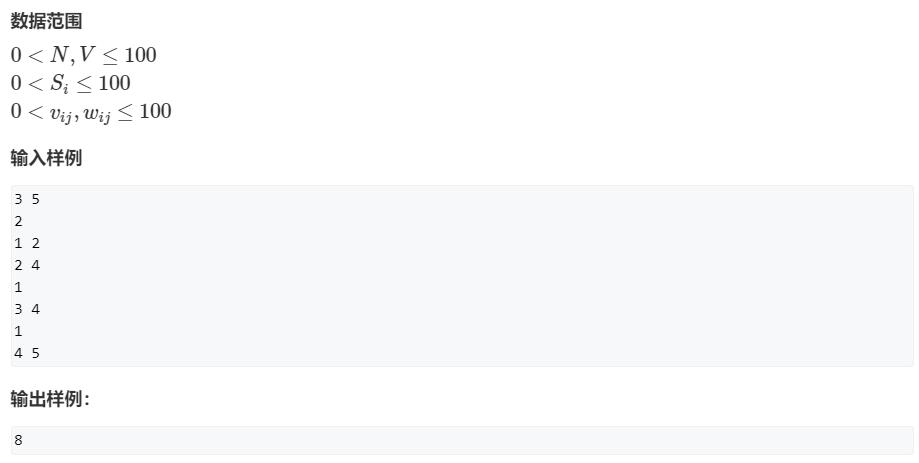
在这里插入图片描述

思路

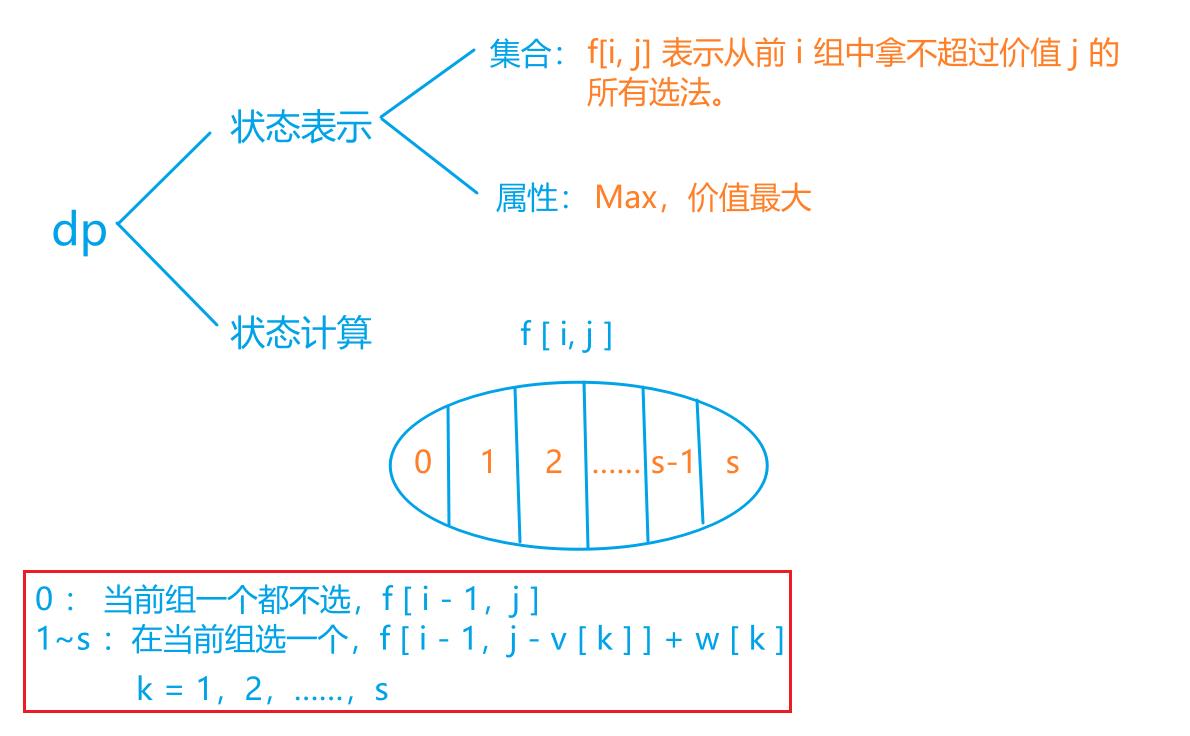
#include <bits/stdc++.h> 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rim int m; scanf("%d", &m)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 110; 
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};

int v[N], w[N], dp[N][N];

int main() {
	//freopen("D:\\\\in.txt", "r", stdin);
	rin;
	rim;
	for (int i = 1; i <= n; ++ i) {
		int s;
		cin >> s;
		for (int j = 1; j <= s; ++ j) {
			cin >> v[j] >> w[j];
		}
		for (int j = 1; j <= m; ++ j) {
			dp[i][j] = dp[i - 1][j];
			for (int k = 1; k <= s; ++ k) {
				if (v[k] <= j) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[k]] + w[k]);
			}
		}
	} 
	cout << dp[n][m];
	return 0;
}

二、线性 DP

AcWing 898. 数字三角形

原题链接：https://www.acwing.com/problem/content/900/
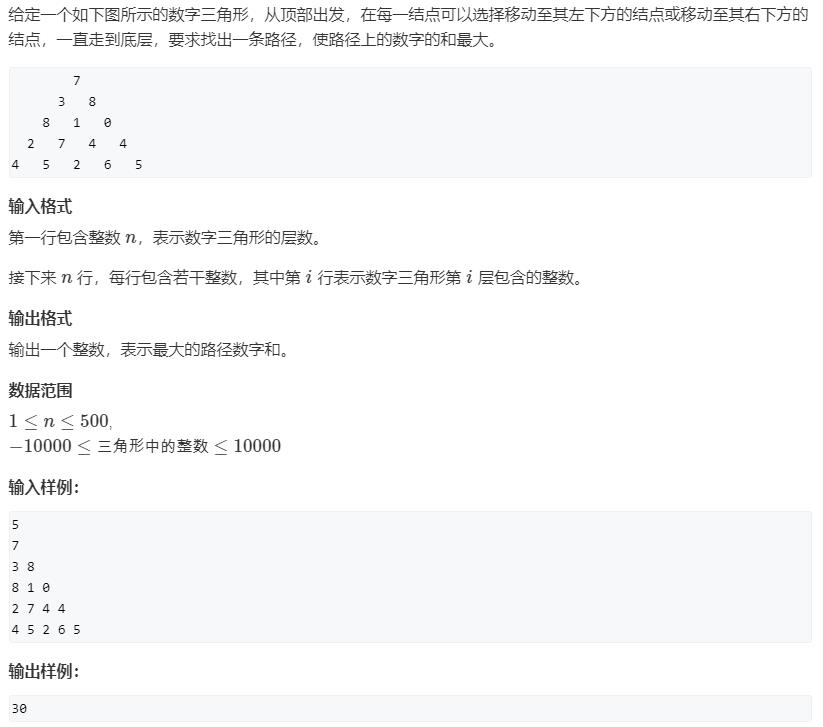
在这里插入图片描述
思路

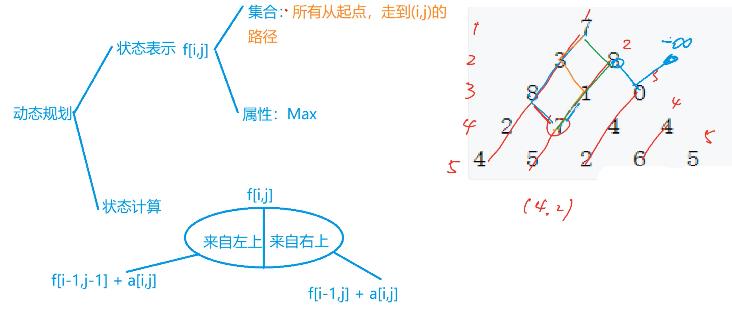
代码

#include<bits/stdc++.h>

using namespace std;

const int N = 510;

int dp[N][N];

int main() {
    int n;
    cin >> n;
    memset(dp, -0x3f3f3f3f, sizeof dp);
    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= i; ++ j) {
            cin >> dp[i][j];
        }
    }
    for (int i = 2; i <= n; ++ i) {
        for (int j = 1; j <= i; ++ j) {
            dp[i][j] += max(dp[i - 1][j - 1], dp[i - 1][j]);
        }
    }
    int ans = -0x3f3f3f3f;
    for (int i = 1; i <= n; ++ i) ans = max(ans, dp[n][i]);
    cout << ans;
    return 0;
}

AcWing 895. 最长上升子序列

原题链接：https://www.acwing.com/problem/content/897/
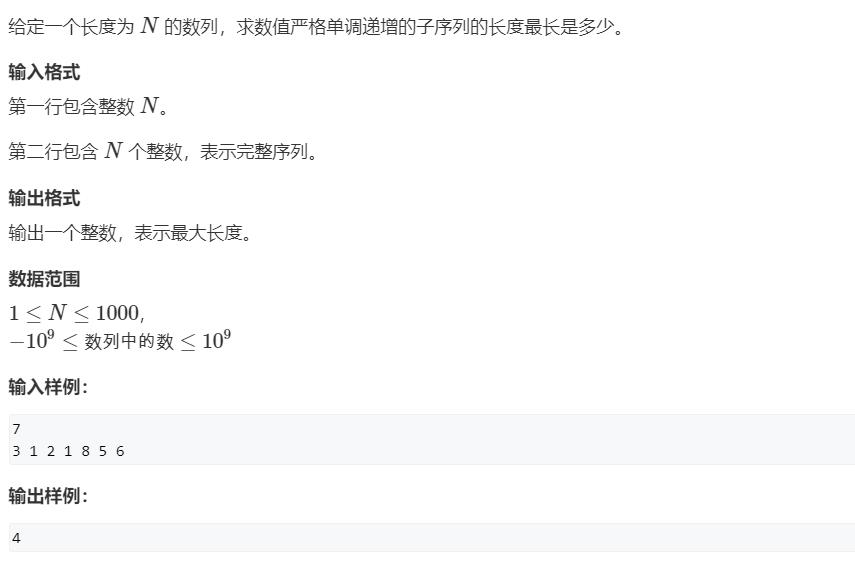
在这里插入图片描述
思路

代码

#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int nums[N], dp[N];

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++ i) {
        cin >> nums[i];
        // 以nums[i]为结尾的递增子序列，则该序列的倒数第二个数必须严格小于nums[i]
        dp[i] = 1;
        for (int j = 1; j < i; ++ j) {
            if (nums[j] < nums[i]) dp[i] = max(dp[i], dp[j] + 1);
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; ++ i) ans = max(ans, dp[i]);
    cout << ans;
    return 0;
}

AcWing 896. 最长上升子序列 II（n = 10^5 nlogn的做法）

原题链接：https://www.acwing.com/problem/content/898/
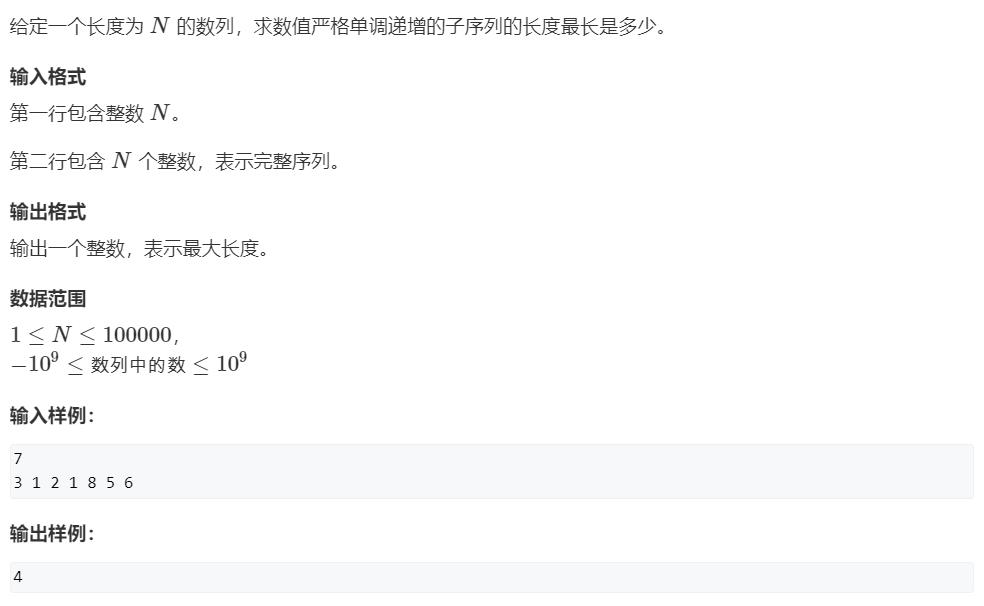
在这里插入图片描述
思路

很显然，该数据范围需要至少在 nlogn 复杂度范围内解决，这里其实已经有点点不像 DP ，更像贪心一点？

我们设有这么一个数组 last [ i ] 表示：在所有长度为 i 的子序列中，最小以 last [ i ] 结尾。
很显然，长度为 a 的子序列，可以看成是长度为 a - 1 的子序列加上 nums [ i ] 而得到的，而能在子序列后面加上 nums [ i ] 的最低标准是，nums [ i ] 必须比所有长度为 a - 1 的子序列的尾数中最小的那个尾数大。

所以综上，二分找出 nums [ i ] 能放在哪一个长度的子序列后面，然后更新 last。

#include<以上是关于ACM - 动态规划小白入门：背包 / 线性 / 区间 / 计数 / 数位统计 / 状压 / 树形 / 记忆化 DP的主要内容，如果未能解决你的问题，请参考以下文章 
 ACM - 动态规划小白入门
 动态规划入门——传说中的零一背包问题
 小白学习动态规划：0-1背包
 ACM：动态规划，01背包问题
 动态规划——背包问题入门
 算法学习——动态规划3