⭐算法入门⭐《动态规划 - 线性DP》简单01 —— LeetCode 746. 使用最小花费爬楼梯

Posted 2021-08-16 英雄哪里出来

🙉饭不食，水不饮，题必须刷🙉
还不会C语言，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？上简单题！ 🧡《C语言入门100例》🧡
LeetCode 太简单？大神盘他！ 🌌《夜深人静写算法》🌌

文章目录

• 一、题目
• • 1、题目描述
  • 2、基础框架
  • 3、原题链接
• 二、解题报告
• • 1、思路分析
  • 2、时间复杂度
  • 3、代码详解
• 三、本题小知识

一、题目

1、题目描述

  数组的每个下标作为一个阶梯，第 $i$ 个阶梯对应着一个非负数的体力花费值 $cost[i]$（下标从 0 开始）。每当爬上一个阶梯，都要花费对应的体力值，一旦支付了相应的体力值，就可以选择 向上爬一个阶梯 或者 爬两个阶梯。求找出达到楼层顶部的最低花费。在开始时，可以选择从下标为 0 或 1 的元素作为初始阶梯。
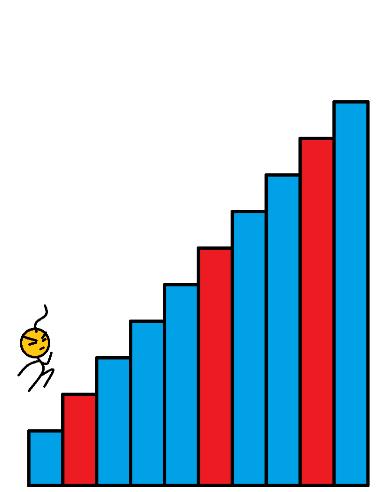
  样例输入： $cost=[1,99,1,1,1,99,1,1,99,1]$
  样例输出： $6$
如图所以，蓝色的代表消耗为 1 的楼梯，红色的代表消耗 99 的楼梯。

2、基础框架

• c++ 版本给出的基础框架代码如下：

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
    }
};

3、原题链接

LeetCode 746. 使用最小花费爬楼梯

二、解题报告

1、思路分析

• 令走到第 $i$ 层的最小消耗为 $f[i]$
• 假设当前的位置在 $i$ 层楼梯，那么只可能从 $i-1$ 层过来，或者 $i-2$ 层过来；
• 如果从 $i-1$ 层过来，则需要消耗体力值：$f[i-1]+cost[i-1]$；
• 如果从 $i-2$ 层过来，则需要消耗体力值：$f[i-2]+cost[i-2]$；
• 起点可以在第 0 或者 第 1 层，于是有状态转移方程：
• $$f[i]=\{\begin{array}{ll}0& i=0,1\\ \min (f[i-1]+cost[i-1],f[i-2]+cost[i-2])& i>1\end{array}$$
  

2、时间复杂度

• 状态数：$O(n)$
• 状态转移：$O(1)$
• 时间复杂度：$O(n)$

3、代码详解

class Solution {
    int f[1100];                                                   // (1)
public:
    int minCostClimbingStairs(vector<int>& cost) {
        f[0] = 0, f[1] = 0;                                        // (2)
        for(int i = 2; i <= cost.size(); ++i) {
            f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]);    // (3)
        }
        return f[cost.size()];
    }
};

• $(1)$ 用f[i]代表到达第 $i$ 层的消耗的最小体力值。
• $(2)$ 初始化；
• $(3)$ 状态转移；

---

三、本题小知识

有没有发现，这个问题和斐波那契数列很像，只不过斐波那契数列是求和，这里是求最小值。

---