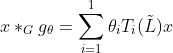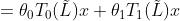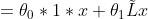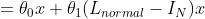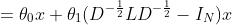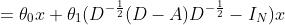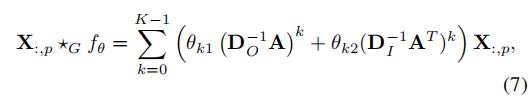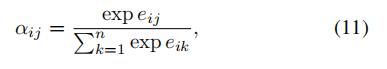交通预测论文翻译：Deep Learning on Traffic Prediction: Methods,Analysis and Future Directions

Posted 2021-08-10 刘文巾

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了交通预测论文翻译：Deep Learning on Traffic Prediction: Methods,Analysis and Future Directions相关的知识，希望对你有一定的参考价值。

原文链接：[2004.08555v3] Deep Learning on Traffic Prediction: Methods, Analysis and Future Directions (arxiv.org)

1 abstract

交通预测在智能交通系统中起着至关重要的作用。准确的交通预测可以辅助路线规划，指导车辆调度，缓解交通拥堵。由于路网中不同区域间复杂而又动态变化的时空依赖性，这一问题具有挑战性。近年来，人们对这一领域进行了大量的研究，特别是深度学习方法，极大地提高了交通预测能力。

本文的目的是从多个角度对基于深度学习的交通预测方法进行全面的调研。具体来说，我们首先总结了现有的流量预测方法，并对其进行了分类。其次，我们列出了不同交通预测应用中最先进的方法。第三，我们全面收集和组织现有文献中广泛使用的公共数据集，以方便其他研究者。此外，我们通过在真实世界的公共数据集上进行大量实验来比较不同方法的性能，从而给出一个评估和分析。最后，我们讨论了这一领域中存在的挑战。

2 introduction

现代城市正逐步向智慧城市发展。城市化进程的加快和城市人口的快速增长给城市交通管理带来了巨大的压力。

智能交通系统是智慧城市的重要组成部分，交通预测是智能交通系统的重要组成部分。准确的交通预测对许多实际应用来说是必不可少的。例如，交通流预测可以帮助城市缓解拥堵;网约车需求预测可以促使汽车共享公司提前将汽车分配到高需求地区。不断增长的可用流量相关数据集为我们提供了探索这一问题的潜在新视角。

2.1 交通预测的挑战性

交通预测是非常具有挑战性的，主要受以下复杂因素的影响:

（1）由于交通数据具有时空性，它不断地随时间和空间变化，具有复杂而又动态变化的时空依赖性。

（1-1）复杂的空间依赖性。从图1可以看出，不同位置对预测位置的影响是不同的，相同位置对预测位置的影响也随着时间的变化而变化。不同位置之间的空间相关性是高度动态的。

图1——复杂的时空相关性。节点表示路网中的不同位置，蓝星节点表示预测目标。颜色越深，与目标节点的空间相关性越大。虚线表示不同时间片之间的时间相关性。

（1-2）动态时间依赖性。同一位置不同时刻的观测值呈现非线性变化，远时间步长的交通状态有时对交通预测准确性的影响要大于近时间步长的交通状态。如图1所示。图1同时指出，流量数据通常呈现出周期性，如封闭性、周期性和趋势性。因此，如何选择最相关的历史观测数据进行预测仍然是一个具有挑战性的问题。

（2）外部因素。交通时空序列数据也受到天气条件、事件或道路属性等外部因素的影响。

2.2 交通预测问题的主要任务

由于交通数据在空间和时间维度上都具有很强的动态相关性，因此挖掘其非线性和复杂的时空特征，进行准确的交通预测是一个重要的研究课题。流量预测涉及到各种应用任务。在此，我们列出了现有交通预测问题的主要应用任务:

（1）交通流

交通流是指在一定时间内通过道路上某一给定观测点的车辆数量。

（2）速度

车辆的实际速度定义为单位时间内行驶的距离。很多时候，由于地理位置、交通条件、驾驶时间、环境、驾驶员个人情况等因素的影响，道路上的每一辆车都会有与周围车辆有不同的行驶速度。

（3）交通需求

交通需求问题是如何使用历史需求数据来预测未来某一个时间片中一个地区的交通需求量。一般使用开始/上车或结束/下车的交通需求量来表示给定时间内一个地区的交通需求。

（4）通行时间

在获取路网中任意两点的路径时，需要估算出行时间。

一般情况下，出行时间应该包括在交通路口的等待时间。

（5）道路占用率

道路占用率表明了车辆占用道路空间的程度，是衡量道路是否得到充分利用的重要指标。

2.3 论文的贡献

这是第一篇从多个角度全面研究基于深度学习的交通预测工作，包括方法、应用、数据集、实验、分析和未来的发展方向。

具体来说，这项调查的贡献可总结如下:

1）我们首先对现有的方法进行分类，介绍了它们的关键模型。

2）我们收集并总结了可用的交通预测数据集。

3）我们进行了比较实验来评估不同的模型，以确定最有效的模型和方法。

4）我们将进一步讨论当前解决方案可能存在的局限性，并列出未来有希望和前景的研究方向。

2.4 现有方法的分类

经过多年的努力，交通预测的研究取得了很大的进展。根据发展过程，这些方法大致可以分为两类:经典方法和基于深度学习的方法。

2.4.1 经典方法

经典的方法包括统计方法和传统的机器学习方法。

统计方法是建立一个数据驱动的统计模型进行预测。最具代表性的算法是历史平均(HA)、自回归综合移动平均(ARIMA)[“Modeling and forecasting vehicular traffific flow as a seasonal arima process: Theoretical basis and empirical results,” 2003]和向量自回归(VAR) [“Vector autoregressive models for multivariate time series,” ，2006 ]。然而，这些方法需要数据满足一定的假设。而时变交通数据过于复杂从而无法满足这些假设。此外，这些方法仅适用于相对较小的数据集。

随后，针对交通预测问题，提出了一些传统的机器学习方法，如支持向量回归(SVR)[ “Forecasting holiday daily tourist flow based on seasonal support vector regression with adaptive genetic algorithm,” 2015]和随机森林回归(RFR)[“Regression conformal prediction with random forests,” 2014]。这些方法具有处理高维数据和捕捉复杂非线性关系的能力。

2.4.2 基于深度学习的方法

直到基于深度学习的方法出现，人工智能在交通预测中的全部潜力才被开发出来[ “Traffific flow prediction with big data: A deep learning approach,” 2015]。该技术研究如何学习一个层次模型，将原始输入直接映射到预期输出[ Deep Learning 2016]。

通常，深度学习模型将基本的可学习块或层堆叠起来，形成一个深度架构，对整个网络进行端到端的训练。为了处理大规模和复杂的时空数据，已经开发了几种体系结构。

一般使用卷积神经网络(Convolutional Neural Network, CNN)[ “Recurrent continuous translation models,” 2013]提取图像或视频描述的网格结构数据的空间相关性，Graph Convolutional Network (GCN)[ “Spectral networks and locally connected networks on graphs,” 2014]将卷积运算扩展到更一般的图结构数据，更适合表示交通网络结构。

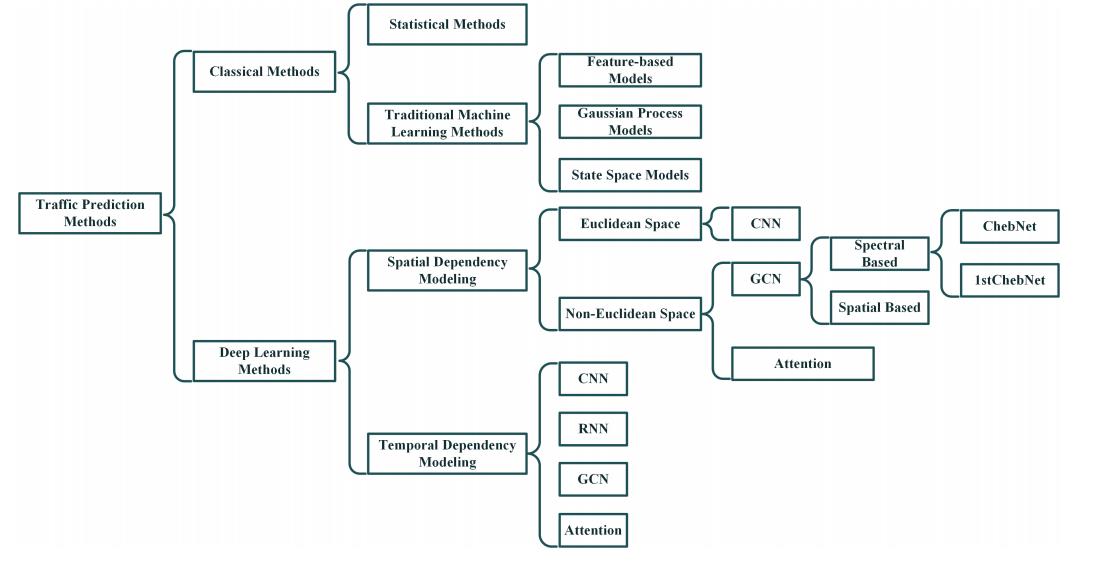
此外，循环神经网络(RNN)[ “Learning representations by back-propagating errors,” 1986 ]、[ “Distributed representations, simple recurrent networks, and grammatical structure,” 1991]及其变体LSTM[ “Long short-term memory,” 1997]或GRU[ “Learning phrase representations using rnn encoder-decoder for statistical machine translation,” 2014]常被用来建模时间相关性。在这里，我们总结了现有交通流量预测方法中常用的关键技术，如下图所示。

2.5 行文的结构

本文的剩余部分的结构如下。

第二节介绍了交通预测的经典方法。

第三节回顾了基于深度学习方法的交通预测工作，包括空间相关和时间相关的常用预测方法，以及其他一些新的变体。

第四节列出了每个任务中的一些有代表性的结果。

第五部分收集和组织流量预测的相关数据集和常用的外部数据类型。

第六节对相关方法进行了比较和评价。

第七节讨论了未来交通预测的几个重要方向。

最后，我们在第八节对本文进行总结。

注：因为我是把abstract当成第一节了，所以论文中的第n节对应的都是我的第n+1节

3 传统方法

统计模型和传统机器学习模型是两种主要的具有代表性的数据驱动的交通预测方法。

在时间序列分析中，自回归综合移动平均(ARIMA)[“Modeling and forecasting vehicular traffific flow as a seasonal arima process: Theoretical basis and empirical results,” 2003]及其变体是基于经典统计的最统一的方法之一，已广泛应用于交通预测问题([“Modeling and forecasting vehicular traffific flow as a seasonal arima process: Theoretical basis and empirical results,” 2003]，[23]-[27])。然而，这些方法一般是针对小数据集，不适合处理复杂的动态时间序列数据。此外，由于通常只考虑时间信息，交通数据的空间依赖性被忽略或很少考虑。

传统的机器学习方法可以建模更复杂的数据，大致分为三类:基于特征的模型、高斯过程模型和状态空间模型。

基于特征的方法通过训练一个基于人工设置的特征的回归模型来解决交通预测问题([28]-[30])。这些方法实现简单，在一些实际情况下可以提供预测。

高斯过程通过不同的核函数对交通数据的内部特征进行建模，这需要同时考虑空间和时间相关性。虽然这种方法在交通预测([31]-[33])中被证明是有效可行的，但与基于特征的方法相比，它们通常具有较高的时间和空间复杂的，这在有大量训练样本时是不合适的。

状态空间模型假定观测结果是由马尔可夫隐态产生的。该模型的优点是可以自然地对交通系统的不确定性进行建模，更好地捕获时空数据的潜在结构。然而，这些模型([34]-[48])的整体非线性是有限的。大多数情况下，它们对复杂的动态交通数据建模不是最优的。表一总结了一些最近有代表性的经典方法。

4 机器学习方法

与传统方法相比，深度学习模型挖掘了数据中更多的特性，使用了复杂的架构，并能获得更好的性能。在表2中，我们总结了现有交通预测方法中的深度学习架构，在本节中我们将回顾这些常见的模型。

4.1 使用空间相关性

4.1.1 CNN

一系列研究将CNN应用于从二维时空交通数据[3]中获取交通网络中的空间相关性。由于交通网络难以用二维矩阵来描述，一些研究试图将不同时刻的交通网络结构转换为图像，并将这些图像划分为标准网格，每个网格代表一个区域。这样，cnn就可以用来学习不同区域之间的空间特征。

如图3所示，每个区域与其附近的区域直接相连。通过3×3窗口，每个区域的邻域是其周围的八个区域。这八个区域的位置指示了一个区域的邻居的顺序。然后，对每个通道的中心区域和它的邻居进行加权平均，将一个过滤器filter应用于这个3×3的“图像块”中。由于相邻区域的特定排序，filter中的可训练权值可以在不同位置之间共享。

在交通路网结构划分中，根据粒度和语义的不同，有许多不同的位置定义。[1]根据经度和纬度将一个城市划分为I× J格网地图，其中一个格网代表一个地区。然后，利用CNN提取不同区域间的空间相关性，进行交通流预测。

4.1.2 GCN

传统CNN仅限于对欧氏数据进行建模，因此GCN用于对非欧氏空间结构数据进行建模，更符合交通路网的结构。GCN一般包括两种方法，基于频谱的方法和基于空间的方法。

基于频谱的方法通过从图信号处理的角度引入滤波器来定义图卷积，其中图卷积运算被解释为从图信号中去除噪声。基于空间的方法将图卷积作为来自邻居的特征信息的聚合。下面我们将分别介绍基于频谱的GCNs和基于空间的GCNs。

4.1.2.1 基于频谱的GCN

Bruna等[18]首先开发了谱图网络，这种结构通过计算图拉普拉斯矩阵L的特征分解，对谱域的图数据进行卷积运算。

具体来说，信号x与滤波器G∈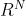 R^N 的图卷积运算∗G可以定义为:

U是标准化图拉普拉斯矩阵 $L_{Normal}$ 的特征向量组成的矩阵

其中标准化图拉普拉斯矩阵 $L_{Normal}$ 被定义成：

$L_{Normal}=D^{-\\frac{1}{2}} L D^{\\frac{1}{2}}=D^{-\\frac{1}{2}} (D-A) D^{-\\frac{1}{2}}=I_N-D^{-\\frac{1}{2}}A D^{-\\frac{1}{2}}$

D是度矩阵，，A是邻接矩阵

见GNN笔记：图卷积_刘文巾的博客-CSDN博客、GNN 笔记：图上的傅里叶变换_刘文巾的博客-CSDN博客

如果我们记基于频谱的图卷积过滤器为，那么上面的图卷积运算可以简化为：

在这个简化式中，一个图信号x通过滤波器g和图变换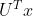 U^Tx 之间的乘积，来进行滤波器g的过滤的。

在这里滤波器g和U之间的乘积是一个时间复杂度为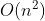 O(n^2) 的计算过程（N*N的两个矩阵，进行矩阵乘法，时间复杂度为 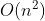O(n^2) ）。后面人们提出了不同的优化策略：

4.1.2.1.1 ChebNet

Defferrard等[49]引入了特征值对角矩阵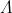 $\\varLambda$ 的切比雪夫多项式作为基于频谱的GCN的滤波器

记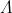 $\\varLambda$ 是由标准化图拉普拉斯矩阵 $L_{Normal}$ 的特征值组成的对角矩阵，那么滤波器有：

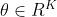$\\theta \\in R^K$ 是一个切比雪夫系数矢量

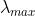$\\lambda_{max}$ 是标准化图拉普拉斯矩阵 $L_{Normal}$ 的最大特征值

切比雪夫多项式的定义为：

于是，此时的图卷积为：

                  $=\\sum_{i=1}^K [\\theta_i T_k(U \\tilde \\varLambda U^T)x]$

                  $=\\sum_{i=1}^K [\\theta_i T_k(U (\\frac{2}{\\lambda_{max}}\\varLambda -I_N) U^T)x]$

                  $=\\sum_{i=1}^K [\\theta_i T_k( (U\\frac{2}{\\lambda_{max}}\\varLambda U^T -UI_N U^T) )x]$

其中（这里的L是前面的 $L_{Normal}$ ）

4.1.2.1.2 一阶ChebNet (1stChebNet)

Kipf和Welling[50]引入的一阶ChebNet近似进一步简化了滤波，假设K = 1， λmax = 2，我们可以得到以下简化表达式:

$x *_G g_\\theta =\\sum_{i=1}^{1}\\theta_i T_i(\\tilde L)x$

$=\\theta_0 T_0(\\tilde L)x +\\theta_1 T_1(\\tilde L)x$

   $=\\theta_0 * 1*x +\\theta_1 \\tilde L x$

   $=\\theta_0 x +\\theta_1 ( L_{normal}-I_N) x$

   $=\\theta_0 x +\\theta_1 (D^{-\\frac{1}{2}}LD^{-\\frac{1}{2}}-I_N)x$

   $=\\theta_0 x +\\theta_1 (D^{-\\frac{1}{2}}(D-A)D^{-\\frac{1}{2}}-I_N)x$

=

θ1和θ2都是可学习的参数

进一步假定，我们有：

为了避免由于层次堆栈操作造成的数值不稳定和爆炸/消失梯度，引入了另一种归一化技术:

其中

于是最终，一个基于谱频的图卷积操作就有了：

其中，是图信号，是滤波器矩阵；C是图信号上单个点的维度数，F是图卷积层滤波器的数量。Z是图信号上点在谱频上的图信号。

4.1.2.1.3基于频谱的图卷积的应用

为了充分利用空间信息,[51]一将交通网络建模成一个一般的图,而不是把它网格化。交通监测点代表图中的节点；监测点之间的连接路径代表图上点与点之间的连接边缘；邻接矩阵则基于站之间的距离来计算得到，这是一种自然、合理的路网规划方法。然后，采用两种基于谱方法的图卷积逼近策略提取空间域的模式和特征，降低了计算复杂度。（就是前面的ChebNet和一阶ChebNet）。

[52]首先使用图来编码区域之间的不同类型的相关性，包括相邻性、功能相似性和交通连通性。然后，利用三组基于ChebNet的GCN分别建模空间相关性，进一步，该模型整合了时间信息，最终达到对交通需求量的预测。

4.1.2.2 基于空域的图卷积

基于空域的图卷积方法通过对中心节点及其邻居进行聚合的过程直接在图上定义卷积，以获得中心节点的新表示，如图4所示。

在[53]中，首先将交通网络建模为有向图，基于扩散过程捕获交通流的动态特征。在此基础上，采用扩散卷积运算（diffusion convolution）对空间相关性进行建模，更加直观地解释了空间相关性，并证明了其在时空建模中的有效性。其中，扩散卷积对双向扩散过程进行建模，使模型能够捕捉上游和下游交通的影响。

扩散卷积这个过程可以定义为:

其中 $X \\in R^{N \\times P}$ 是图信号，N是节点的数量，P是图上每个节点的特征数量， $X_{:,p}$ 则代表了第p个特征。

是扩散卷积算子

k是进行的扩散卷积的次数（一共要进行K次扩散卷积）

$f_\\theta$ 是K次扩散卷积的参数，这个参数可学习

$\\theta \\in R^{K \\times 2}$ ,由后面的 $\\theta_{k1},\\theta_{k2}$ 组成

分别代表了出度矩阵和入度矩阵

对于多维特征的输入和输出，我们可以有：

其中 $Z \\in R^{N \\times Q}$ 是扩散卷积的输出

$\\theta \\in R^{Q \\times P \\times K \\times 2}$ 是整个扩散卷积的参数（Q代表输出的维度，P代表输入的特征数量，K代表了进行扩散卷积的次数，2是出度矩阵和入度矩阵）

基于扩散卷积过程，[54]设计了一种新的神经网络层，可以映射不同维度特征的变换，提取空域的模式和特征。

[55]利用自适应邻接矩阵修正了[53]中的扩散过程，允许模型自行挖掘隐藏的空间相关性。

[56]引入了聚合的概念来定义图卷积。该操作可以将每个节点的特征与其相邻节点的特征进行组合。聚合函数是一个线性组合，其权值等于节点与其相邻节点之间的边的权值。这个图的卷积运算可以表示为:

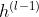$h^{(l-1)}$ 是第l层图卷积层的输入，W和b都是参数，A是邻接矩阵，σ是激活函数

4.1.3 注意力机制

注意力机制最早被提出用于自然语言处理[57]，然后被广泛应用于各个领域。

一条道路的交通状况受其他道路不同影响程度的影响。这种影响是高度动态的，随着时间的推移而变化。为了建模这些属性，空间注意机制经常被用来自适应捕获道路网络中区域之间的相关性([58]-[66])。其关键思想是在不同的时间步长动态地为不同的区域分配不同的权重。

为了简单起见，我们暂时忽略时间坐标。注意机制作用于一组输入序列x = (x1，…， xn)，其中每个 $x_i \\in R^{d_x}$ (是x的维度），计算一个新序列z = (z1，…， zn)，其中 $z_i \\in R^{d_z}$ 。每个输出元素zi被计算为输入元素的加权和:

加权系数 $\\alpha_{ij}$ 表明了xi点对于xj点交通流量的重要程度，并且是用以下的方式计算得到的（softmax）：

$e_{ij}$ 是用以下的方式计算得到的：

这里，v，,，b都是可学习的参数

这种机制被证明是有效的，但是当一个序列中元素的个数n很大时，我们需要计算个权重系数，因此时间和内存消耗很大。（每一对<i,j>点对都需要一组参数，n个点就有个<i,j>点对，所以需要组权重系数。

在交通速度预测中，[60]利用注意力机制动态捕获目标区域与路网一阶相邻区域之间的空间相关性。

[67]将基于ChebNet的GCN与注意力机制相结合，充分利用交通网络的拓扑特性，动态调整不同区域之间的相关性。

4.2 使用时间相关性

4.2.1 CNN

[68]首次使用了完全卷积模型以用于序列到序列学习的。

[51]使用纯卷积结构同时从图结构的时间序列数据中提取时空特征，是交通研究领域的代表作。

另外，扩展因果卷积（dilated causal convolution）是一种特殊的标准一维卷积。它通过改变扩张速率的值来调整感受野的大小，这有利于捕获长期的周期依赖性。因此[69]和[70]采用扩展因果卷积作为其模型的时间卷积层，以捕获节点的时间趋势。

与循环模型相比，卷积创建的是固定大小上下文的表示。然而，通过层层叠加，网络的有效上下文大小可以很容易地变大。这可以让使用者较为精确地控制要建模的相关项的最大长度。

卷积网络不依赖于前一个时间步长的计算，所以它允许并行化序列中的每个元素，这样可以更好地利用GPU硬件，更容易优化。这优于rnn, rnn需要保持过去的全部隐藏状态，因而RNN较难进行序列的并行计算。

4.2.2 RNN

RNN及其变体LSTM或GRU是用来处理序列数据的神经网络。为了建模交通数据的非线性时间依赖性，基于rnn的方法被应用于交通预测[3]。这些模型依赖于数据的顺序来依次处理数据，因此这些RNN模型的一个缺点是，当建模长序列时，它们记住在许多时间步之前所学内容的能力可能会下降。

在基于rnn的序列学习中，一种称为编码器-解码器（encoder-decoder）的特殊网络结构被应用于交通流量预测([53]，[58]，[61]-[66]，[71]-[79])。其关键思想是将源序列编码为固定长度的向量，并使用解码器生成交通预测结果。

f是编码器，g是解码器。

表示t时刻可以看到的输入信息

s是经过了编码器encoder之后的向量表示

$\\hat{X}_{t+1:t+L}$ 表示L步之前的预测结果

θ1和θ2都是可学习参数

编码器-解码器结构的一个潜在问题是，无论输入和输出序列的长度如何，编码和解码之间的语义向量的长度总是固定的，因此当输入信息太长时，一些信息将丢失。

4.2.3 ATTENTON

为了解决上述问题，一个重要的改进是使用时间域上的注意力机制，该机制可以自适应地选择它认为重要的编码器相关隐藏状态来产生输出序列。这与空间方法中的注意类似。这种时间注意机制不仅可以对路网中某一位置的当前交通状况与以往观测数据之间的非线性相关性进行建模，还可以对长期序列数据进行建模，解决RNN的不足。

[62]设计了一种时间注意力机制来自适应地建模不同时间步长之间的非线性相关性。

[67]结合了标准卷积和注意力机制，通过融合相邻时间步长处的信息来更新节点的信息，从语义上表达了不同时间步长之间的依赖关系。

考虑到交通数据具有高度的周期性，而不是严格的周期性，[80]设计了一种周期性转移注意机制来处理长时间片段的周期性依赖，和周期性的时间转移。

4.2.4 GCN

Song[56]等人首先构造了一个包含时间和空间属性的局部时空图，然后利用提出的基于空间的GCN方法同时建模时空相关性。

4.3 时空关系同时考虑

如表2所示，大多数交通预测方法使用混合深度学习框架，它们结合不同类型的技术分别捕获交通数据的空间相关性和时间相关性。它们假定地理信息和时间信息的关系是独立的，没有考虑它们的联合关系。因此，没有充分利用时空相关性来获得更好的精度。

为了解决这一限制，研究人员试图将时空信息整合到邻接图矩阵或张量中。例如，[56]通过将所有节点在前一刻和后一时刻的状态与当前时刻的状态连接，得到了一个局部的时空图。根据局部时空图的拓扑结构，可以直接捕获各个节点与其时空邻居之间的相关性。

在[81]中，Fang等针对不同连接的历史交通状况、邻居之间连接的特征和历史时隙的特征构造了三个矩阵，其中矩阵的每一行对应一条连接的信息。最后，将这三个矩阵串联成一个矩阵，并将其重塑为一个三维时空张量。然后利用注意机制得到交通状态之间的关系。

4.4 深度学习+传统模型

近年来，越来越多的研究将深度学习与经典方法相结合，一些先进的方法被用于交通预测([82]-[85])。这种方法不仅弥补了经典模型非线性表示能力较弱的缺点，也弥补了深度学习方法解释性差的缺点。

[82]提出了一种基于状态空间生成模型和基于滤波器的模型推理方法。它利用深度神经网络实现发射模型和过渡模型的非线性，利用递归神经网络实现随时间的依赖性。这种基于参数化的非线性网络提供了处理任意数据分布的灵活性。

[83]提出了一种深度学习框架，这种框架将矩阵分解方法引入到深度学习模型中，可以对潜在区域函数以及区域间的相关性进行建模，进一步提高了城市全区域流量预测的模型能力。

[84]开发了一种混合模型，该模型将由时间深度网络规范化的全局矩阵分解模型与捕获每个维度特定模式的局部深度时间模型相关联。通过针对每个维度的数据驱动关注机制，将全局模型和局部模型结合起来。因此，可以利用数据的全局模式，并与局部定标相结合，更好地进行预测。

[85]结合潜在模型和多层感知器(MLP)设计了一个网络，用于解决多变量时空时间序列预测问题。该模型在空间和时间层面上捕捉了多个序列的动态和相关性。

表3总结了深度学习和经典方法结合的相关文献。

4.5 基于深度学习的模型的不足之处

深度神经网络模型的优点使其非常有吸引力，确实极大地促进了交通预测领域的进展。然而，与传统方法相比，它也有一些缺点。

4.5.1 高数据需求。

深度学习高度依赖于数据，通常数据量越大，它的性能就越好。在很多情况下，这些数据是不容易获得的，例如，一些城市可能发布数年的出租车数据，而另一些城市可能只发布几天的数据。

4.5.2 较高的计算复杂度。

深度学习对计算能力的要求很高，普通cpu已经不能满足深度学习的要求。主流计算采用GPU和TPU。同时，随着模型复杂度和参数数量的增加，对内存的需求也逐渐增加。一般来说，深度神经网络比经典算法在计算上更昂贵。

4.5.3 缺乏可解释性。

深度学习模型通常被认为是“黑盒”，缺乏可解释性。一般而言，深度学习模型的预测精度高于经典方法。然而，目前鲜有办法没有解释为什么会得到这些结果，以及如何确定参数以使结果更好。

5 代表性结论

在本节中，我们将总结不同交通预测任务的一些有代表性的结果。基于研究不同交通预测任务的文献，我们列出了目前常用公共数据集下的最佳性能方法，如表IV所示。

我们可以观察到:

第一，在相同的预测任务下，不同数据集上的结果有很大的差异。例如，在交通需求预测任务中，在相同的时间间隔和预测时间下，NYC Taxi和TaxiBJ数据集的准确率分别为8.385和17.24。

第二，在预测任务和数据集相同的情况下，性能随着预测时间的增加而下降，Q-Traffic的速度预测结果显示。（也就是预测约久远的未来，精度越差）

第三，对于同一数据源的数据集，由于选择的时间和地区不同，对精度也有较大的影响，例如速度预测任务下基于PeMS相关数据集的精度。

第四，在不同的预测任务中，速度预测任务的准确率一般可以达到90%以上，显著高于准确率接近或超过80%的其他任务。因此，这些工作仍有很大的改进空间。

一些公司目前正在进行智能交通研究，如高德、滴滴、百度地图。

根据2019年高德地图技术年报[119]，高德地图在导航应用中开展了深度学习的探索与实践。不同于一般的历史平均方法，深度学习考虑了历史数据呈现的时效性和年周期性特征。通过在产品实践中引入时态卷积网络(TCN)[120]模型，并结合特征工程(提取动态和静态特征，引入年周期性等)，成功解决了现有模型的不足。给定一周，周中的到达时间是基于订单数据测量的，它的坏情况率为10.1%，比基准线低0.9%。对于未来一小时的出行时间预测，[117]设计了一个多模型体系结构，利用即将到来的交通流数据，通过添加上下文信息来推断未来的出行时间。利用高德地图上的匿名用户数据，北京的MAPE可以减少到16%左右。

预计到达时间(ETA)、供求和速度预测是滴滴平台的关键技术。滴滴在ETA中应用了人工智能技术，利用神经网络和滴滴的海量订单数据，将MAPE指数降低到11%，实现了在实时大规模请求下为用户提供准确的到达时间预期和多策略路径规划的能力。

在预测和调度方面，滴滴利用深度学习模型预测未来一段时间后的供求差异，并提供司机调度服务。对未来30分钟供需缺口的预测准确率达到85%。

在城市道路速度预测任务中，滴滴提出了基于行驶轨迹标定的预测模型[121]。通过基于滴滴盖亚数据集中成都和西安数据的对比实验，可以将速度预测的总体MSE指标分别降至3.8和3.4。

百度通过将辅助信息集成到深度学习技术中，解决了在线路线查询中的流量预测任务，发布了基于百度地图的离线和在线辅助信息的大规模流量预测数据集[73]。该数据集交通速度预测的总体MAPE和2小时后交通速度预测的MAPE分别下降到8.63%和9.78%。

在[81]中，百度的研究者提出了端到端神经框架作为移动地图应用中出行时间预测的产业解决方案，旨在探索和利用交通预测中的时空关系和上下文信息。以太原市、合肥市和惠州市百度地图为样本的MAPE分别为21.79%、25.99%和27.10%，这个结论证明了该模型的优越性。该模型已经在百度地图上投入生产，每天成功处理数百亿个请求。

6 公共数据集

高质量的数据集对于准确的交通预测是必不可少的。在本节中，我们全面总结了用于交通预测任务的公共数据信息，主要包括两部分:一部分是预测中常用的公共时空序列数据，另一部分是用来提高交通预测精度的外部数据。但是，由于不同的模型框架的设计或数据的可用性，后一种数据并不是所有模型都需要或者可以使用。

6.1 公共数据集

在这里，我们列出了用于交通预测的公共、常用和大规模真实数据集。

6.1.1 PEMS

PeMS是加州交通运输局测量系统(California Transportation Agency Performance Measurement System，简称PeMS)的缩写，该数据系统在地图上显示，并由39000多个独立探测器实时采集。这些传感器跨越了加州所有主要城市的高速公路系统。其来源为:http://pems.dot.ca.gov/。在此基础上，出现了多个子数据集版本(PeMSD3/4/7(M)/7/8/-SF/-BAY)，并得到了广泛的应用。主要区别在于时间和空间的范围，以及数据采集中包含的传感器的数量。

PeMSD3:该数据集是Song等人处理的一段数据。包括358个传感器和2018年1月9日至2018年11月30日的流量信息。处理过的版本可以在 https://github.com/Davidham3/STSGCN 上找到。

PeMSD4:它描述了旧金山湾区的交通数据。从2018年1月1日到2018年2月28日，共59天，在29条道路上安装了3848个传感器。处理过的版本可以在https://github.com/Davidham3/ASTGCN/tree/master/data/PEMS04 上找到。

PeMSD7(M):描述了加州第七区的交通数据，包含228个站点，时间范围为2012年5月和6月的工作日。处理过的版本可以在https://github.com/Davidham3/STGCN/tree/master/datasets上找到。

PeMSD7:该版本由Song等人公开发布。包含883个传感器站的交通流信息，时间跨度为2016年1月7日至2016年8月31日。处理过的版本可以在https://github.com/Davidham3/STSGCN上找到。

PeMSD8:它描绘了圣贝纳迪诺地区的交通数据，包含了从2016年7月1日到2016年8月31日共62天的8条道路上的1979个传感器。处理过的版本可以在https://github.com/Davidham3/ASTGCN/tree/master/data/PEMS08上找到。

PeMSD-SF:该数据集描述了旧金山海湾地区高速公路不同车道的车辆占用率，在0到1之间。这些测量的时间跨度从2008年1月1日到2009年3月30日，数据每10分钟采样一次。其来源为:http://archive.ics.uci.edu/ml/datasets/PEMS-SF。

PeMSD-BAY:包含从2017年1月1日到2017年6月30日6个月的交通速度统计数据，包括湾区的325个传感器。其来源为:https://github.com/liyaguang/DCRNN。

6.1.2 METR-LA

它记录了从2012年3月1日到2012年6月30日四个月的交通速度统计数据，包括洛杉矶县高速公路上的207个传感器。其来源为:https://github.com/liyaguang/DCRNN。

6.1.3 LOOP

这些数据来自大西雅图地区4条连接的高速公路(I-5、I-405、I-90和SR- 520)上安装的环路检测器。它包含了整个2015年323个传感器站的交通状态数据，每5分钟一次。其来源为:https://github.com/zhiyongc/Seattle-Loop-Data。

Los-loop:该数据集由环路检测器在洛杉矶县的高速公路上实时收集。它包括207个传感器，其交通速度从2012年3月1日到2012年3月7日采集。这些交通速度数据每5分钟汇总一次。资料来源如下:https://github.com/lehaifeng/T-GCN/tree/master/data.

6.1.4 TaxiBJ

轨迹数据是2013年7月1日- 2013年7月30日、2014年3月1日- 2014年6月30日、2015年3月1日- 2015年6月30日、2015年11月1日- 2016年4月10日四个时段的北京市出租车GPS数据和北京的气象数据。资料来源:https://github.com/lucktroy/DeepST/tree/master/ data/TaxiBJ。

6.1.5 SZ-taxi

这是2015年1月1日至1月31日深圳出租车的运行轨迹。它包含罗湖区156条主要道路作为研究区域。每条道路上的交通速度每15分钟计算一次。其来源为:https://github.com/lehaifeng/T-GCN/tree/master/data。

6.1.6 NYC Bike

自行车的轨迹是从纽约市CitiBike系统收集的。共有约13000辆自行车和800个站点。其来源为:https://www.citibikenyc.com/systemdata。处理过的版本可以在https://github.com/lucktroy/DeepST/tree/master/data/BikeNYC上找到

6.1.7 NYX Taxi

轨迹数据是2009年至2018年纽约市出租车GPS数据。其来源为:https://www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page。

6.1.8 Q-trafffic

该数据集由查询子数据集、交通速度子数据集和路网子数据集三部分组成。这些数据收集于2017年4月1日至2017年5月31日中国北京百度地图。其来源为:https://github.com/JingqingZ/BaiduTraffic#Dataset。

6.1.9 芝加哥

这是2013年到2018年芝加哥共享单车的发展轨迹。其来源为:https://www.divvybikes.com/system-data。

6.1.10 BikeDC

这是来自于华盛顿的自行车系统。数据集包括2011年、2012年、2014年和2016年4个时段472个站点的数据。其来源为:https://www.capitalbikeshare.com/system-data。

6.1.11 ENG-HW

它包含了英国政府记录的三个城市之间城际公路的交通流信息，时间范围为2006年至2014年。其来源为:http://tris.highwaysengland.co.uk/detail/trafficflowdata。

6.1.12 T-Drive

它由2015年2月1日至2015年6月2日北京出租车的大量轨迹组成。这些轨迹可以用来计算每个区域的交通流量。资料来源:https://www.microsoft.com/en us/research/publication/t-drive-driving direction -based on taxi-trajectories/。

6.1.13 I-80

这是2005年4月13日在加利福尼亚州埃默里维尔市的旧金山湾区东行I-80号公路上收集的详细车辆轨迹数据。数据集时长45分钟，车辆轨迹数据每十分之一秒提供研究区域内每辆车的精确位置。其来源为:http://ops.fhwa.dot.gov/trafficanalysistools/ngsim.htm。

6.1.14 滴滴出行

DiDi 盖亚数据开放项目为学术界提供真实、免费的脱敏数据资源。主要包括多城市出行时间指数、出行和轨迹数据集。其来源为:https://gaia.didichuxing.com。

6.1.14.1 Travel Time Index data（滴滴）

数据集包括深圳、苏州、济南、海口4个城市的出行时间指数，包括市级、区级和道路级的出行时间指数和平均行驶速度，时间范围为2018年1月1日至2018年12月31日。包括滴滴打车平台2018年1月10日至12月1日在成都、西安二环路区域的轨迹数据，以及区域内道路级、成都、西安市级的出行时间指数和平均行车速度。并包含成都和西安2018年1月1日至2018年12月31日的市级、区级、道路级出行时间指数和平均行车速度。

6.1.14.2 出行数据

该数据集包含海口市2017年5月1日至2017年10月31日的每日订单数据，包括订单开始和结束的经度和纬度，以及订单类型、出行类别和客流量的订单属性。

6.1.14.3 轨迹数据

该数据集来自于2016年10月和11月的滴滴打车平台在西安和成都二环地区的订单司机轨迹数据。轨迹点采集间隔为2 ~ 4s。对轨迹点进行了道路绑定处理，确保数据与实际道路信息相对应。司机和订单信息经过了加密、脱敏和匿名处理。

6.2 公共外部数据

流量预测往往受到许多复杂因素的影响，这些因素通常被称为外部数据。这里，我们列出了常见的外部数据项。

1）天气条件:温度、湿度、风速、能见度和天气状态(晴天/雨天/刮风/多云等)

2）驾驶员ID:

由于驾驶员个人条件的不同，预测会有一定的影响，因此有必要对驾驶员进行标记，而这一信息主要用于个人预测。

3）特殊事件:包括各种节日、交通管制、交通事故、体育赛事、音乐会等活动。

4）时间信息:星期几，一天中的时间。

(4.1)工作日(day-of-week)由于其特殊性，通常包括工作日和周末。

(4、2) time-of-day一般有两种划分方法，一种是通过实证检验训练数据集中时间的分布，可以直观地将一天中的24小时划分为3个时段:高峰时段、非高峰时段和睡眠时段。另一种是手动将一天划分为几个时间段，每个时间段对应一个时间间隔。

7 实验分析和讨论

在本节中，我们对几种基于深度学习的交通预测方法进行了实验研究，以识别每个模型中的关键组成部分。为此，我们利用metro - la数据集进行交通速度预测，评估在该数据集上使用公共代码的最新方法，并研究性能限制。

7.1 实验配置

在实验中，我们在一个公共数据集上比较了六种典型的速度预测方法和公共代码的性能。表V总结了相关比较方法的公共源代码链接。

Approach	Link
STGCN [51]	https://github.com/VeritasYin/STGCN IJCAI-18
DCRNN [53]	https://github.com/liyaguang/DCRNN
ASTGCN [67]	https://github.com/guoshnBJTU/ASTGCN-r-pytorch
Graph WaveNet [55]	https://github.com/nnzhan/Graph-WaveNet
STSGCN [56]	https://github.com/Davidham3/STSGCN
GMAN [62]	https://github.com/zhengchuanpan/GMAN

metra - la数据集:该数据集包含207个传感器，采集了2012年3月1日至2012年6月30日4个月的实验数据。70%的数据用于训练，20%用于测试，剩余的10%用于验证。交通速度的数据汇总为5分钟间隔的数据，并应用Z-Score进行归一化。在构建路网图时，将每个交通传感器视为一个节点，节点的邻接矩阵由具有阈值的高斯核计算而得[122]。

我们使用以下三个度量标准来评估不同的模型:平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)。

$\\hat{y}^i$ 和 $y^i$ 分别代表了点i的预测值和真实值

$\\xi$ 则是总节点的数量

对于比较算法中的超参数设置，我们根据相应文献([51]，[53]，[55]，[56]，[62]，[67])中的实验设置其值。

7.2 实验结果和分析

在本节中，我们对各种先进的交通速度预测方法在图结构数据上的性能进行了评估，未来15分钟、30分钟、60分钟(T= 3,6,12)的预测结果如表VI所示。

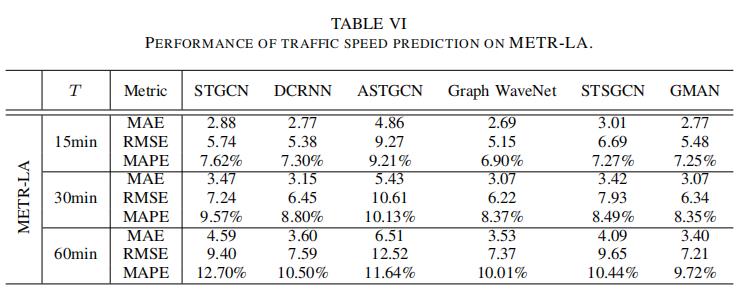
STGCN应用ChebNet图卷积和1D卷积提取空间相关性和时间相关性。

ASTGCN在STGCN的基础上利用两个注意力层分别捕获交通网络在空间维度和时间维度上的动态关联。

DCRNN是一种前沿的深度学习预测模型，在训练阶段利用扩散图卷积网络和RNN学习空间依赖关系和时间关系的表示。

Graph WaveNet将图卷积与扩展随机卷积相结合，以捕获时空相关性。

STSGCN基于局部时空图的邻接矩阵同时提取局部时空相关信息。

GMAN在空间和时间维度上使用纯注意力结构来建模动态的时空关联。

由表VI中的实验结果可以看出:

首先，基于注意力的方法(GMAN)在空间相关性提取方面优于其他基于gcn的方法。

在空间相关性建模时，GCN使用sum、mean或max函数来聚合每个节点邻居的特征，忽略了不同邻居的相对重要性。相反，注意机制引入加权的思想，根据邻居信息的重要性，实现不同时刻节点的自适应更新，取得了较好的效果。

第二，谱域上的GCN模型(STGCN和ASTGCN)的性能普遍低于空域上的GCN模型(DCRNN、Graph WaveNet和STSGCN)。

第三，大多数方法的结果在预测15min后的交通流量时没有显著差异，但随着预测时间长度的增加，基于注意力的方法(GMAN)的表现明显优于其他基于GCN的方法。

由于大多数现有的方法以迭代的方式预测交通状况，它们的性能在短期预测中可能不会受到很大影响，因为用于预测的所有历史观测都是无错误的。

但是，由于长期预测需要用到之前预测过的一些交通流量，这会导致误差积累，大大降低了预测的准确性。

由于注意力机制可以直接进行多步预测，因此无论是短期预测还是长期预测，都可以使用正确的观测结果，而不需要使用容易出错的预测值。

因此，上述观测结果为提高预测精度提供了可能的途径。

首先，注意力机制可以更有效地提取路网空间信息。

其次，在使用GCN时，基于空间的方法通常比基于谱域的方法更有效。

第三，在建立时间相关性模型时，注意力机制对提高长期预测性能更有效。

值得一提的是，当外部数据可用时，添加外部数据组件还有助于提高性能。

7.3 时间复杂度分析

为了评估计算复杂度，我们在metra - la数据集上比较了这些模型的计算时间和参数数量。

所有实验都是在12GB内存的特斯拉K80上进行的，每种方法的批数（batch）统一设置为64,T设置为12，我们计算了一个epoch的平均训练时间。为了进行推断，我们计算验证数据上的时间成本。结果见表7。

STGCN采用全卷积结构，训练速度最快。

DRCNN采用循环结构，非常耗时。

相对于STGCN、DCRNN、ASTGCN、STSGCN等需要迭代计算才能产生12个预测结果的方法，Graph WaveNet可以在一次运行中提前预测12步，因此需要更少的推断时间。

STSGCN将三个不同时刻的图合并成一个图作为邻接矩阵，大大增加了模型参数的数量。

GMAN是由多个注意力机制组成的纯注意力机制模型，因此需要计算多个变量对之间的关系，因此参数的数量也较高。

需要注意的是，由于模型设计比较复杂，在计算GMAN的计算时间时，在我们的设备上显示“out of memory”。

8未来展望

虽然近年来交通预测取得了很大的进展，但仍有许多开放性的挑战没有得到充分的研究。这些问题需要在今后的工作中加以解决。在接下来的讨论中，我们将阐述未来进一步研究的一些方向。

8.1 数据稀少问题

大多数现有的交通预测解决方案需要大量地数据。然而，异常情况(比如极端天气、临时交通控制等)通常是非周期性的，难以获取数据，这使得训练样本量比正常交通情况下更小，学习难度更大。

此外，由于不同城市的发展水平不均衡，很多城市存在数据不足的问题。然而，充分的数据通常是深度学习方法的先决条件。

一个可能的解决方案是使用迁移学习技术来执行跨城市的深度时空预测任务。该技术旨在有效地将知识从数据丰富的源城市转移到数据匮乏的目标城市。虽然最近已经提出了一些方法([70]，[91]，[123]，[124])，但这些研究还没有得到深入的研究，如如何设计一个高质量的数学模型来匹配两个区域，或者如何整合其他可用的辅助数据源等，仍然值得考虑和研究。

8.2 交通知识图谱

知识图谱是知识融合的重要工具。它是由大量的概

以上是关于交通预测论文翻译：Deep Learning on Traffic Prediction: Methods,Analysis and Future Directions的主要内容，如果未能解决你的问题，请参考以下文章

事件相机与计算机视觉论文分享--Event-based Vision meets Deep Learning on Steering Prediction for Self-driving Car

论文翻译：2020_A Robust and Cascaded Acoustic Echo Cancellation Based on Deep Learning

论文精读A Survey on Deep Learning for Named Entity Recognition

论文导读- E-LSTM-D: A Deep Learning Framework for Dynamic Network Link Prediction（动态网络链接预测）

论文笔记-Deep Learning on Graphs: A Survey（上）

paper：Traffic Flow Prediction With Big Data: A Deep Learning Approach SAE模型