paper：Traffic Flow Prediction With Big Data: A Deep Learning Approach SAE模型
Posted David_7788
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了paper：Traffic Flow Prediction With Big Data: A Deep Learning Approach SAE模型相关的知识，希望对你有一定的参考价值。
Autoencoder
理论讲解
paper的任务是基于历史的交通数据预测未来的交通流量数据，并且发现交通流量的数据是具有一定的周期性的，因此其提出了 SAE的模型，其希望可以先记住交通流量的数据，然后在进行推导
paper提出的SAE的流程图
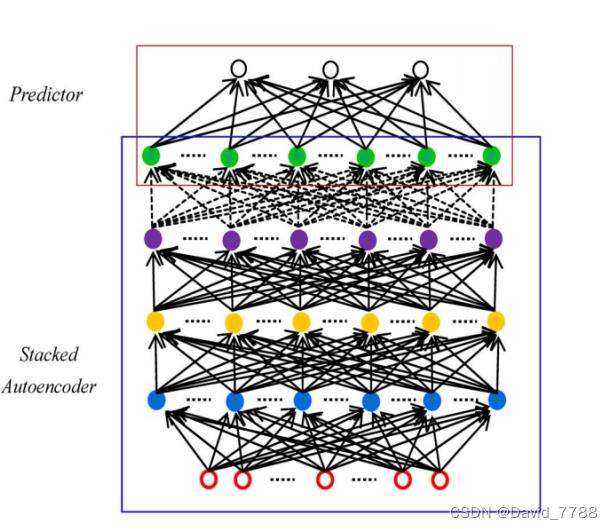
通过堆叠的Autoencoder自编码器来进行预测的任务
Autoencoder 的模型
y ( x ) = f ( W 1 x + b ) Z ( x ) = g ( W 2 y ( x ) + c ) y(x)=f(W_1x+b)~~~~~~Z(x)=g(W_2y(x)+c) y(x)=f(W1x+b) Z(x)=g(W2y(x)+c)
预训练
Autoencoder自编码器在预训练的时候是一个逐层贪心算法，而且是无监督的算法，在预训练阶段，自编码器的目标就是可以重现输入，即输出和输入要尽可能相同，并且在训练阶段，其每一次只训练一个网络层，训练好了该层，然后再训练下一个网络层，直到整个网络所有的层都训练完成后，才开始整个网络一起进行训练微调。
但是由于输入的维度可能会隐藏层的维度要小，导致直接记住每一个数据，只有部分权重起作用，但是paper不希望这样，因此他在loss中加入了KL散度，来惩罚这样的事情。
S
A
O
=
L
(
X
,
Z
)
+
γ
∑
j
=
1
H
D
K
L
(
ρ
∣
∣
ρ
^
j
)
K
L
(
(
ρ
∣
∣
ρ
^
j
)
=
ρ
l
o
g
ρ
ρ
j
^
+
(
1
−
ρ
)
l
o
g
1
−
ρ
1
−
ρ
j
^
L
(
X
,
Z
)
表示的就是
l
o
s
s
，
γ
是一个平衡参数，
ρ
是一个超参数，
ρ
^
是数据进过了该层后的平均值
SAO=L(X,Z)+γ∑^H_D_j=1KL(ρ||\\hatρ_j) \\\\ KL((ρ||\\hatρ_j)=ρlog\\fracρ\\hatρ_j+(1-ρ)log\\frac1-ρ1-\\hatρ_j\\\\ L(X,Z)表示的就是loss，γ是一个平衡参数，ρ是一个超参数，\\hatρ是数据进过了该层后的平均值
SAO=L(X,Z)+γj=1∑HDKL(ρ∣∣ρ^j)KL((ρ∣∣ρ^j)=ρlogρj^ρ+(1−ρ)log1−ρj^1−ρL(X,Z)表示的就是loss，γ是一个平衡参数，ρ是一个超参数，ρ^是数据进过了该层后的平均值
KL散度（相对熵），用来衡量两个分布之间的差异（分布1：以超参数ρ为均值对构成的伯努利分布，分布2：所有的训练集的data通过hidden_layer后的值的平均为均值的伯努利分布，之间的差异）由于loss函数中有使用所有训练集data在通过hidden_layer后的平均值后计算的，因此得先过一遍训练集，然后才可以正常预训练
真正训练
真正训练的时候就是有监督的算法，输入数据，输出预测，与label进行计算loss，然后反向传播，更新参数，与普通的网络算法没什么区别
但是注意Autoencoder预训练时候包括x–>y，输入到隐藏层；y–>z，隐藏层到输出层，但是真正训练的时候只有x–>y，而y–>z则不包含。
代码讲解
参数
sae=SAE()
loss_fn=nn.MSELoss()
optimizer=optim.Adam(sae.parameters(),lr=1e-3)
seq_len=96 # 已知的时间序列的长度
pred_len=96 # 预测的时间序列的长度
epoches=10
rou=0.005
预训练代码
计算经过该层网络后的平均激活，也就是计算过了该层网络后的数据的平均值
# 计算平均激活，就是经过当前层后的值的平均值，在计算KL散度的时候会使用
def rou_hat_cala(i,self,xx):
'''
Args:
（i//2）+1 是训练哪一层fc
self是使用哪个网络（sae）
xx是输入数据
'''
if i == 0:
pred = torch.sigmoid(self.fc1(xx))
rou_hat1 = torch.mean(pred) + 1e-5 # 计算loss时需要使用,加上一个很小的数，防止为0
elif i == 2:
pred = torch.sigmoid(self.fc1(xx))
pred = torch.sigmoid(self.fc2(pred))
rou_hat1 = torch.mean(pred) + 1e-5 # 计算loss时需要使用,加上一个很小的数，防止为0
elif i == 4:
pred = torch.sigmoid(self.fc1(xx))
pred = torch.sigmoid(self.fc2(pred))
pred = torch.sigmoid(self.fc3(pred))
rou_hat1 = torch.mean(pred) + 1e-5 # 计算loss时需要使用,加上一个很小的数，防止为0
elif i == 6:
pred = torch.sigmoid(self.fc1(xx))
pred = torch.sigmoid(self.fc2(pred))
pred = torch.sigmoid(self.fc3(pred))
pred = torch.sigmoid(self.fc4(pred))
rou_hat1 = torch.mean(pred) + 1e-5 # 计算loss时需要使用,加上一个很小的数，防止为0
elif i == 8:
pred = torch.sigmoid(self.fc1(xx))
pred = torch.sigmoid(self.fc2(pred))
pred = torch.sigmoid(self.fc3(pred))
pred = torch.sigmoid(self.fc4(pred))
pred = torch.sigmoid(self.fc5(pred))
rou_hat1 = torch.mean(pred) + 1e-5 # 计算loss时需要使用,加上一个很小的数，防止为0
else:rou_hat1=0
return rou_hat1
预训练的完整代码
首先先把所有的层都冻住，requires_grad=False，这里我和理论讲解处不同的地方在于，我是经过整个网络后计算输出和输入的loss，而不是经过一层计算输入和输出的loss，即我这里不会而外增加从隐藏层到输出的FC
开始进行逐层训练，一次只训练一层网络，require_gard=Ture，然后都是根据公式按部就班的计算，改层网络训练50个epoches，然后就把这一层网络冻住，开始训练下一层网络
#预训练,把不训练的其它层全部冻住（requires_grad=Fasle）
def pre_train(self,train_data):
rou_hat = 0
param_lst=[] #把每一层的权重的名字装起来
#将所有的可训练参数全部设置为False
for param in self.named_parameters(): #name_parameters()会返回层名字和权重
param[1].requires_grad=False
param_lst.append(param[0])
for i in range(len(param_lst)):
lst=list(self.named_parameters())#得到网络权重和名称
if i%2==0:
lst[i][1].requires_grad=True
lst[i+1][1].requires_grad=True #逐层训练
total_len= pred_len + seq_len
#把训练集的数据都经过一遍网络，然后在计算经过隐藏层的平均激活
for j in range(train_data.shape[0] // total_len): # 总共可以取多少个total_len
x = train_data[j * total_len:(j + 1) * total_len, :] # 每一次取total长度
xx = x[:seq_len, :].clone() # 每一次已知的时间序列（seq_len,dim）
xx = xx.unsqueeze(0) # 升维度（1,seq_len,dim）
xx = xx.permute(0, 2, 1) # 输出维度是（1,dim,seq_len）
#计算rou_hat，平均激活
rou_hat+=rou_hat_cala(i,self,xx)
rou_hat=rou_hat/(j+1)+1e-5 # +1e-5是为了为0
for epoch in range(epoches):
runing_loss = 0
for j in range(train_data.shape[0] // total_len): # 总共可以取多少个total_len
x = train_data[i * total_len :(i + 1) * total_len, :] # 每一次取total_len长度
xx = x[:seq_len, :].clone() # 每一次已知的时间序列（seq_len,dim）
xx = xx.unsqueeze(0) # 升维度（1,seq_len,dim）
xx = xx.permute(0, 2, 1) # 输出维度是（1,dim,seq_len）
pred = sae(xx) # 输出是（1,dim,seq_len）
optimizer.zero_grad()
pred = pred.squeeze()
pred=pred.permute(1,0)#输出是(seq-len,dim)
kl=rou*torch.log(rou/rou_hat)+(1-rou)*torch.log((1-rou)/(1-rou_hat)) #计算KL散度
loss = loss_fn(pred, x[seq_len:, :])+kl # 计算loss
loss.backward()
runing_loss += loss
optimizer.step()
rou_hat = rou_hat_cala(i, self, xx)
print('第0个epoch的loss：1'.format(epoch + 1, round((runing_loss / (i + 1)).item(), 2)))
lst[i][1].requires_grad = False
lst[i + 1][1].requires_grad = False # 把训练好的层再次冻住
逐层训练完毕后，整一个网络整体进行训练，进行微调，这一部分就和普通的网络进行训练一样
def train(net,loss_fn,optimizer,train_data,seq_len,pred_len,epoches):
'''
Args:
net是需要训练的网络
loss_fn是使用的损失函数，train_data是整个训练集
seq_len是已知的时间序列的长度，pred_len是需要预测的时间序列长度
epoches是外循环多少次，
'''
net.train()
total_len=pred_len+seq_len
for epoch in range(epoches):
runing_loss = 0
for i in range(train_data.shape[0] // total_len): # 总共可以取多少个total_len
x=train_data[i*total_len:(i+1)*total_len,:]#每一次取total_len长度
xx=x[:seq_len,:].clone()#每一次已知的时间序列（seq_len,dim）
xx=xx.unsqueeze(0)#升维度（1,seq_len,dim）
xx=xx.permute(0,2,1)#输出维度是（1,dim,seq_len）
pred=net(xx)#输出是（1,dim,pred_len）
optimizer.zero_grad()
pred=pred.contiguous().squeeze(0).permute(1,0)#输出是（pred_len,dim）
loss=loss_fn(pred,x[seq_len:,:])#计算loss
loss.backward()
runing_loss+=loss
optimizer.step()
print('第0个epoch的loss：1'.format(epoch+1,round((runing_loss/(i+1)).item(),2)))
预训练完毕后，把相应的权重进行保存
正式训练的时候可以直接调用预训练的权重
Autoencoder正式训练的代码
模型初始化
初始化五个全连接层，这一个也没什么特别的，这里可以调用之前预训练好的权重
class Autoencoder(nn.Module): #输入是已知的时间序列，输出是预测时间序列
def __init__(self,args,hidden_size=300):
'''
Arg:
seq_len=96代表输入数据的第二个维度（时间维度：已知多长的时间序列）
pred_len=96代表预测时间有多长,hidden_size=300是隐藏层的神经元数量
'''
super(Autoencoder, self).__init__()
seq_len=args.seq_len
pred_len=args.pred_len
# 输入是（batch_size,dim,seq_len）-->输出为（batch_size,dim,hidden_size）
self.fc1=nn.Linear(seq_len,hidden_size)
# 输入是（batch_size,dim,hidden_size）-->输出为（batch_size,dim,hidden_size）
self.fc2=nn.Linear(hidden_size,hidden_size)
# 输入是（batch_size,dim,hidden_size）-->输出为（batch_size,dim,hidden_size）
self.fc3=nn.Linear(hidden_size,hidden_size)
# 输入是（batch_size,dim,hidden_size）-->输出为（batch_size,dim,hidden_size）
self.fc4=nn.Linear(hidden_size,hidden_size)
# 输入是（batch_size,dim,hidden_size）-->输出为（batch_size,dim,pred_len）
self.fc5=nn.Linear(hidden_size,pred_len)
forward部分的代码，把五个全连接连接在一起，最后输出预测值
def forward(self, enc_x, enc_mark, y, y_mark):
'''
Args:
:param enc_x: 已知的时间序列 （batch_size,seq_len,dim）
以下的 param本 model未使用，不做过多介绍
:param enc_mark: 已知的时序序列的时间对应的时间矩阵，
:param y:
:param y_mark:
:return: x_cat_pred[:,-self.pred_len:,:] 将预测的时间序列的部分返回回去 (batch_size,pred)len,dim)
'''
enc_x=enc_x.permute(0,2,1) # 输入为（batch_size,seq_len,dim）--》输出为（batch_size,dim,seq_len）
x=torch.sigmoid(self.fc1(enc_x)) # 输入是（batch_size,dim,seq_len）-->输出为（batch_size,dim,hidden_size）
x=torch.sigmoid(self.fc2(x)) # 输入是（batch_size,dim,hidden_size）-->输出为（batch_size,dim,hidden_size）
x=torch.sigmoid(self.fc3(x)) # 输入是（batch_size,dim,hidden_size）-->输出为（batch_size,dim,hidden_size）
x=torch.sigmoid(self.fc4(x)) # 输入是（batch_size,dim,hidden_size）-->输出为（batch_size,dim,hidden_size）
x=self.fc5(x) # 输入是（batch_size,dim,hidden_size）-->输出为（batch_size,dim,pred_len）
x=x.permute(0,2,1)#输入是（batch_size,dim,pred_len）输出是（batch_size,pred_len,dim）
return x #返回值的shape是（batch_size，pred_len，dim）
数据压缩网络
根据Autoencoder的特性，另一个思路就是根据Auencoder进行数据压缩，压缩过后的数据在送入LSTM中进行预测任务
class SAE(nn.Module):
def __init__(self,arg):
super(SAE, self).__init__()
self.arg=arg
# 先使用SAE_encoder把数据的时间维度进行压缩，压缩为hidden_size2，即从seq_len-->hidden_size2
self.SAE_encoder=SAE_encoder(seq_len=self.arg.seq_len,hidden_size1=72,hidden_size2=48)
# 将经过SAE_encoder压缩过后的数据，放入LSTM中进行预测任务
self.LSTM=LSTM(seq_len=48,pred_len=self.arg.pred_len,dim=self.arg.d_feature,hidden_size=128,num_layers=1,batch_size=self.arg.batch_size)
def forward(self,enc_x, enc_mark, y, y_mark):
'''
:param enc_x: 已知的时间序列 （batch_size,seq_len,dim）
以下的 param本 model未使用，不做过多介绍
:param enc_mark: 已知的时序序列的时间对应的时间矩阵，
:param y:
:param y_mark:
:return: x 将预测的时间序列的部分返回回去 (batch_size,pred_len,dim)
'''
# 其中预训练是使用自编码器的方法进行预训练
self.SAE_encoder.load_state_dict(torch.load('./checkpoint/SAE/SAE_encoder')) # 使用预训练的SAE_encoder的权重
x=self.SAE_encoder(enc_x) # x shape(batch_size,dim,hidden_size2),seq_len被压缩为hidden_size2, 为了方便后面的seq_len都是表示hidden_size2
x=x.permute(2,0,1)#输出为（seq_len,batch_size,dim）
x=self.LSTM(x)#输出是（pred_len,batch_size,dim）
x=x.permute(1,0,2)#输出是（batch_size,pred_len,dim）
return x
首先数据压缩网络也没有什么特别的，就是几个全连接神经网络将数据的时间维度进行了压缩
class SAE_encoder(nn.Module):
def __init__(self,seq_len=96,hidden_size1=72,hidden_size2=48):
'''
Arg:
seq_len=96代表输入数据的第二个维度（时间维度：已知多长的时间序列）
hidden_size1=72是隐藏层1的神经元数量，hidden_size2=48是隐藏层2的神经元数量
其中hidden_size2就是经过SAE_encoder压缩过后的数据的时间维度
'''
super(SAE_encoder, self).__init__()
# 输入是(batch_size,in_channels,seq_len)-->输出为(batch_size,in_channels,hidden_size1)
# 其中in_channels表示的是数据的特征维度,本任务中为7
self.hidden1=nn.Linear(seq_len,hidden_size1)
# 输入是(batch_size,in_channels,hidden_size1)-->输出为（batch_size,in_channels,hidden_size2）
self.hidden2=nn.Linear(hidden_size1,hidden_size2)
def forward(self,x):
x=x.permute(0,2,1) # 对输入数据x进行转置，处理的是seq_len维度
x=torch.relu(self.hidden1(x)) # 输出为(batch_size,in_channels,hidden_size1)
x=self.hidden2(x) # 输出为（batch_size,in_channels,hidden_size2）
return x
数据压缩过后送入LSTM网络中
初始化LSTM网络
class LSTM(nn.Module):#输入的数据维度（seq_len，batch_size,dim),因为使用了SAE进行数据压缩，把时间维度从seq_len变成hidden_size2
def __init__以上是关于paper：Traffic Flow Prediction With Big Data: A Deep Learning Approach SAE模型的主要内容，如果未能解决你的问题，请参考以下文章
交通预测论文笔记《Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting》
Discrete Mathematics and Its Applications | 1 CHAPTER The Foundations: Logic and Proofs | 1.4 Predic
torch.max()函数predic = torch.max(outputs.data, 1)[1].cpu().numpy()