Acwing 236. 格鲁吉亚和鲍勃（博弈论妙题）

Posted 2021-08-08 Jozky86

Acwing 236. 格鲁吉亚和鲍勃

题意：

一排网格，将网格从左到右依次编号 1,2,3，…，并将 N 个西洋棋棋子放在不同的网格上，如下图所示：

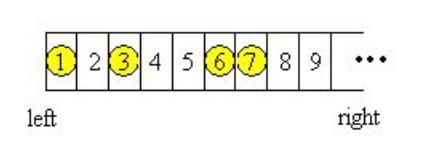
两个人轮流移动棋子
每次玩家选择一个棋子，并将其向左移动，但是不能越过任何其他西洋棋棋子或超过左边界。

玩家可以自由选择棋子移动的步数，其限制是棋子必须至少移动一步，一个网格最多可以包含一个棋子。

无法移动任何棋子的玩家将输掉游戏。
1<=N<=1000
每个棋子的位置不超过10000

题解：

看题目可知，每个棋子的位置不超过10000 ，说明状态可以达到2¹⁰⁰⁰⁰,那用sg函数记忆化搜索求无法实现，这么大的范围，说明题目会有更为精妙的解法

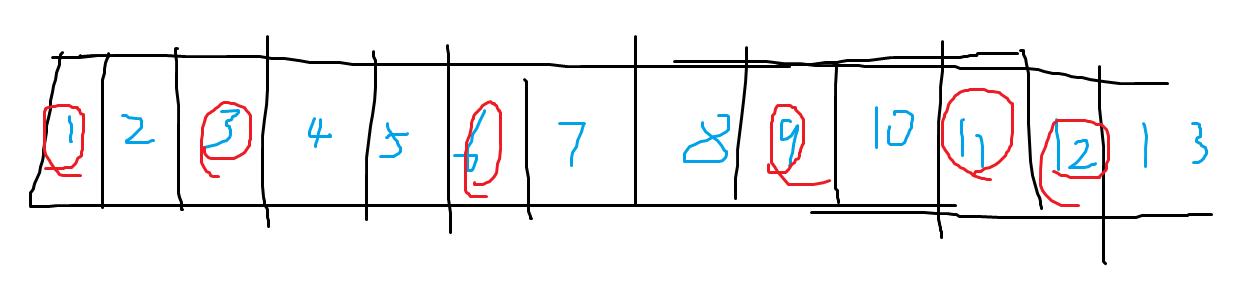
如图，红色圈住的为棋子所在位置，我们考虑6和9这两个位置的棋子，如果先手移动6位置的棋子x步，那么后手也可以移动9位置的棋子x步，相当于后手可以复制前者的操作，相当于大家都没操作。但是如果先手移动9，后手就不一定可以复制先手的操作，你可能会问为什么先手移动9，后者为社么不一定能够11呢？我们这里是将两个棋子为一组看待的，6和9为一组，如果先手移动9，后手移动其他组的棋子(比如11)，那先手还可以移动那个组剩下的棋子(比如12)，这样消除了后手刚刚的操作，因此比赛的关键取决于每组的间隙。如果是奇数个呢？我们就让第一个棋子与左边界为一组，剩下偶数个相邻两两一组。
这样问题就变成了：
假设现在有m组，每组都有空隙大小为a[i]，每次操作可以减小任意一组的空隙大小(1~a[i]),两个人轮流操作，如果有一方无法操作，则游戏结束
现在这个游戏像什么？不就是nim游戏吗？再想想是不是，所有我们直接将空隙大小异或就可以得到游戏结果
妙啊这个题的思路

代码：

#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\\n",a,b);
typedef long long ll;
using namespace std;

inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);
   return s*w;
}
int main()
{
	int t;
	cin>>t;
	while(t--){
		int n;
		cin>>n;
		for(int i=1;i<=n;i++)cin>>a[i];
		if(n&1)a[++n]=0;
		sort(a+1,a+1+n);
		int s=0;
		for(int i=2;i<=n;i+=2){
			s^=(a[i]-a[i-1]-1);
		}
		if(s)cout<<"Georgia will win"<<endl;
		else puts("Bob will win");
		
	} 
	return 0;
}