新版白话空间统计（13）：随机的力量

Posted 2022-06-21 虾神说D

CSDN的被爬虫专用声明：虾神原创，公众号\\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。

前文再续，书接上一回，先请出本节镇文神图：

看到这张图，可能很多同学会问，随机不是没有分析的意义么？你这里的完美的是啥意思捏？难道说要让我们的数据都表现成随机才好么？

那么我们今天来好好聊聊随机的力量。

首先，校正一个观念——啥叫随机？

有的同学看见随机，第一反应就是随机不就是乱么，乱的没有任何规律，乱得没有办法分析和预测？

好吧，如果你是这样认为的，也不能说全是错的，但是没有认识到随机的核心含义。

随机的核心是什么呢？

随机代表的不是乱，指的是不预先设定任何立场，不代表任何特定情况。它表示了所有的情况出现的概率是均等的，无法通过常识和经验进行预测。

其疾如风，其徐如林，侵掠如火，不动如山，难知如阴，动如雷震。

——孙子兵法，军争篇

最著名的随机，就是所谓的素数——它随机的出现在数轴的位置上，没有任何规律，无法预测。

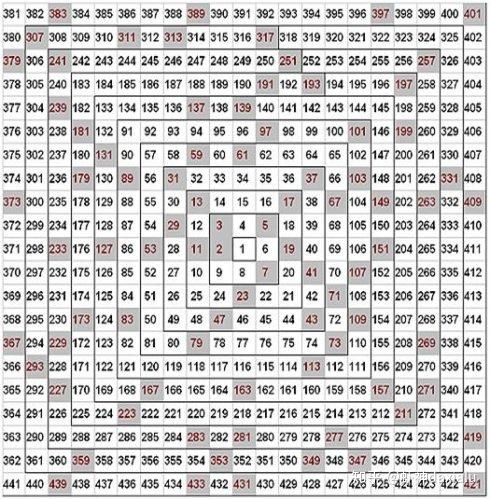
在空间统计学上，我们的随机指的有两个含义：

1、是在空间上，某个要素出现的位置没有规律，在整个研究区域内所有位置出现的概率都是均等的。

2、在属性上，空间位置不发生变化的情况下，某个特定要素的值（可以分为高值以及低值）出现的在任何空间位置上的概率是均等的。

所以，空间统计学上，空间位置和要素属性，二者共同作用，所形成的规律才是空间分布规律，任何一方的特性都不能判定为随机分布，如下图所示：

如果不看属性，那么妥妥的是随机分布（废话，虾神我就是用创建随机数工具生成的）。

那么，如果给上这样的属性值呢：

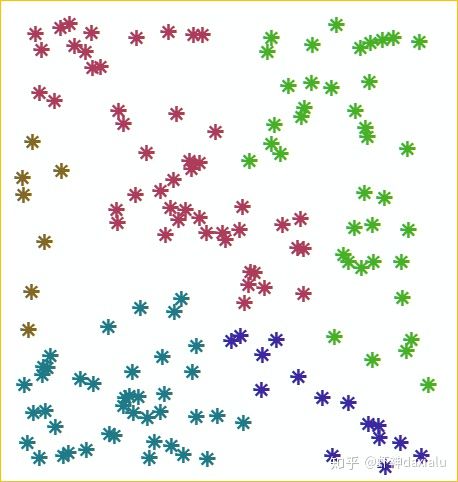
那么我们发现，就是妥妥的聚集分布了——每个要素旁边，大概率出现的都是类似（同一类）的要素。

或者下面这样的分布：

从空间上看，绝对的聚集分布——在四个角上的聚集区，数据的密度远高于平均值。但是如果在属性上这样：

那么就又变成随机的分布了。

从上面这个例子，我们可以简单的做出如下在总结（划重点，要考）：

1、在空间统计里面，判断空间分布（聚集、离散、随机）的关键，在于空间关系与属性信息的共同作用。

2、空间关系决定了分布的判定基础，它定义两个要素之间是否存在相邻关系

3、属性信息决定了空间分布的判定结果，它决定了最终样本之间的分布模式。

看到这里，不知道有没有同学会想到这样一个问题，比如我们要计算某个种群，比如就是某个树种的空间分布吧：

因为同一个树种，可以视他们的值都是一样的，那么你怎么算，都有可能是不正确的，比如你用距离计算，指定一个比较小的距离，得到的结果可能就是离散，而用比较大的距离，得到的结果可能就是聚集。用一个中等距离，那么得到的就是随机。（虽然有三种不同的可能，但是从理论上说都是正确的，因为不同的空间关系定义，肯定会带来不同的结果。）——这里下挖个坑，等我们讲空间关系矩阵的时候，会详细说明，当然，如果等不及新版，可以看旧版文章：

那么有没有一个比较客观的分析思路，来判断这个树种到底呈现什么分布呢？还是一样，所谓“抛开计量谈毒性就是耍流氓”，抛开空间尺度谈空间关系也是耍流氓……

 

所以我们可以先定义一个固定的空间尺度，比如我下面所示的，我设置1.5*1.5公里为一个格网，然后按照该格网里面，是否有该树种，把数据转换了这种二值化的格网数据：

 

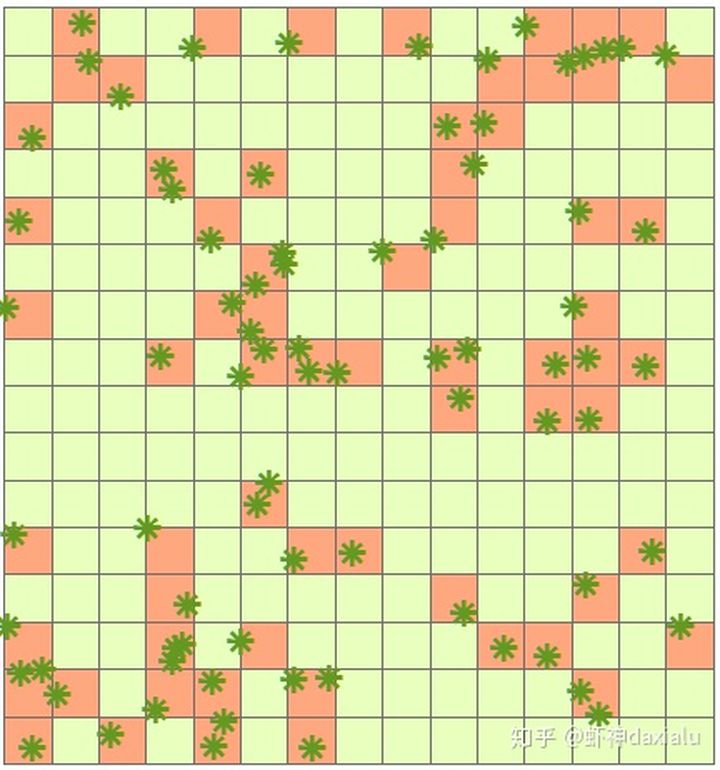
之后我们就可以用这种格网数据来做空间自相关来判断数据的分布情况了，这种方法也被叫做joinCount算法，等不及看新版的，也可以看以前我写过的旧版文章：

当然，我们在做这种种群类分析的时候，肯定不能只有一个种群的，所以我们可以把其他的数据也给加上来，比如下面这种：

 

 

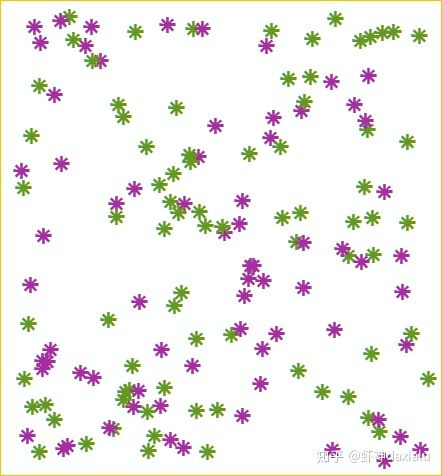
绿色代表我们需要分析的种群，水红色代表其他的种群，这样就可以很轻易的分析出结果来了。

好吧，说到这里我突然发现我跑题了……后面这两种分析分析应该在其他的章节里面讲，所以我们继续回归正题。

我们继续说随机的力量。

刚才说到了某个树种的空间分布，那么我们想，怎么样的分布，才是健康的呢？聚集？离散？还是随机？我们把这三种模式对比做成下面的表格：

特征描述优点缺点聚集该树种分布呈现聚集模式，表示有群居性特征，可能是因为对某些生在条件具有比较苛刻的需求因为大部分树种都会集中在某个区域内，所以比较容易寻找、管理、保护。对生存条件比较苛刻，也容易遭受各种灾害的侵袭。随机分布呈现随机模式，表示该树种对生存环境无特殊要求，在任何地方都有被发现的可能树种的生存能力强，没有特别的条件需求。不容易集中进行保护和管理。离散分布呈现离散模式，表示该树种有比较强烈的生存竞争性。另外可能与其他树种有比较好的相生性。适合于其他树种（物种）搭配种植，形成良好的生态圈。物种本身可能比较稀少，且不容易保护。

从一个物种的生存能力上看，最健壮的肯定是随机——到处都有。但是一般来说，随机分布的物种，都具有很强的生存能力——比如野草、灌木。

自然界是这样，那么社会学研究中呢？也是一样，如下面这个例子：

我们在研究教育公平性的时候，通常会用学校同年级之间的平均分来进行研究，假设在一个城市中，我们所有学区的生源质量、教育水平和师资力量都是均等的话，那么理论上应该是呈现随机分布，也就是所有区域出现高分学生和低分学生的概率都是均等。

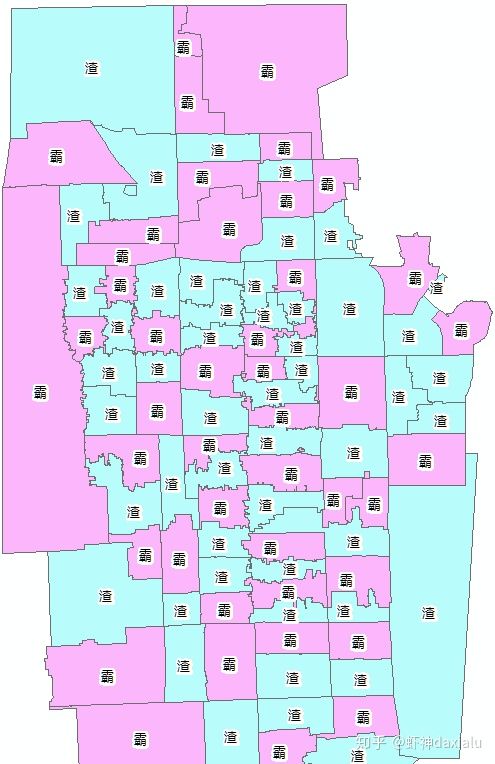
这是比较合理的分布，学霸区和学渣区呈现随机分布。

但是实际上我们发现，会呈现这两类状态的会比较多：

第一种就是学霸区打堆，其他都是学渣区……

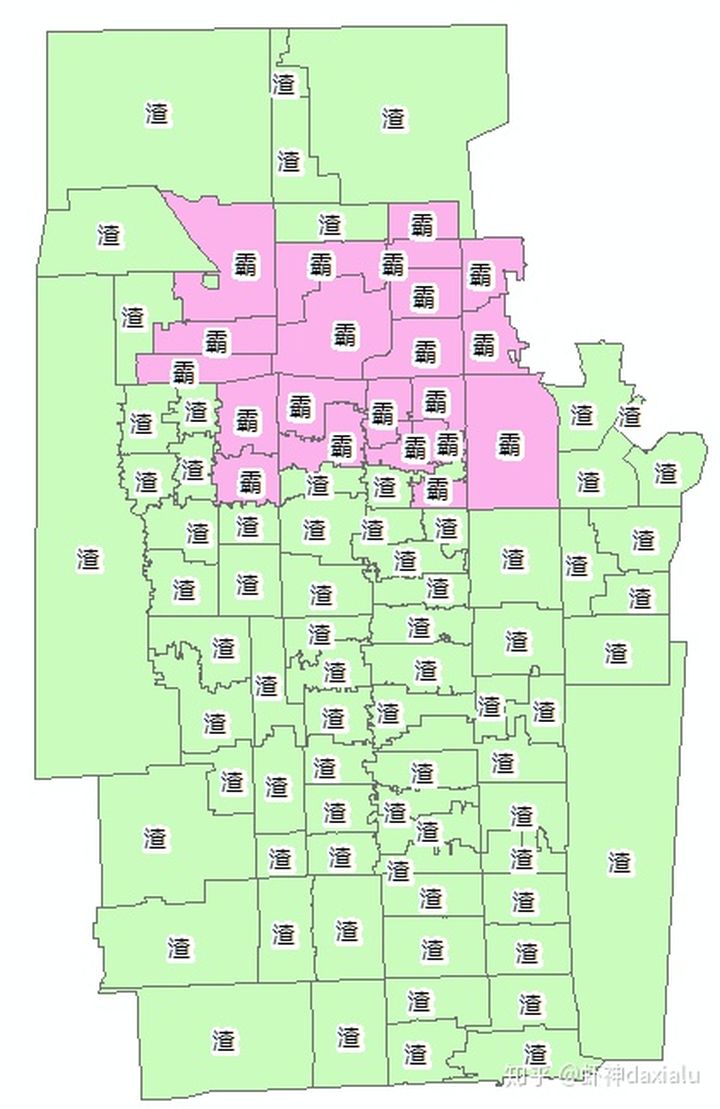
以上的分布是妥妥的聚集分布，学渣和学渣打堆，学霸和学霸打堆，酱油和酱油扎堆。那么这种分布确实，实际上也是一种教育资源不均衡的体现了，但是还有更夸张的，比如这样的分布：

 

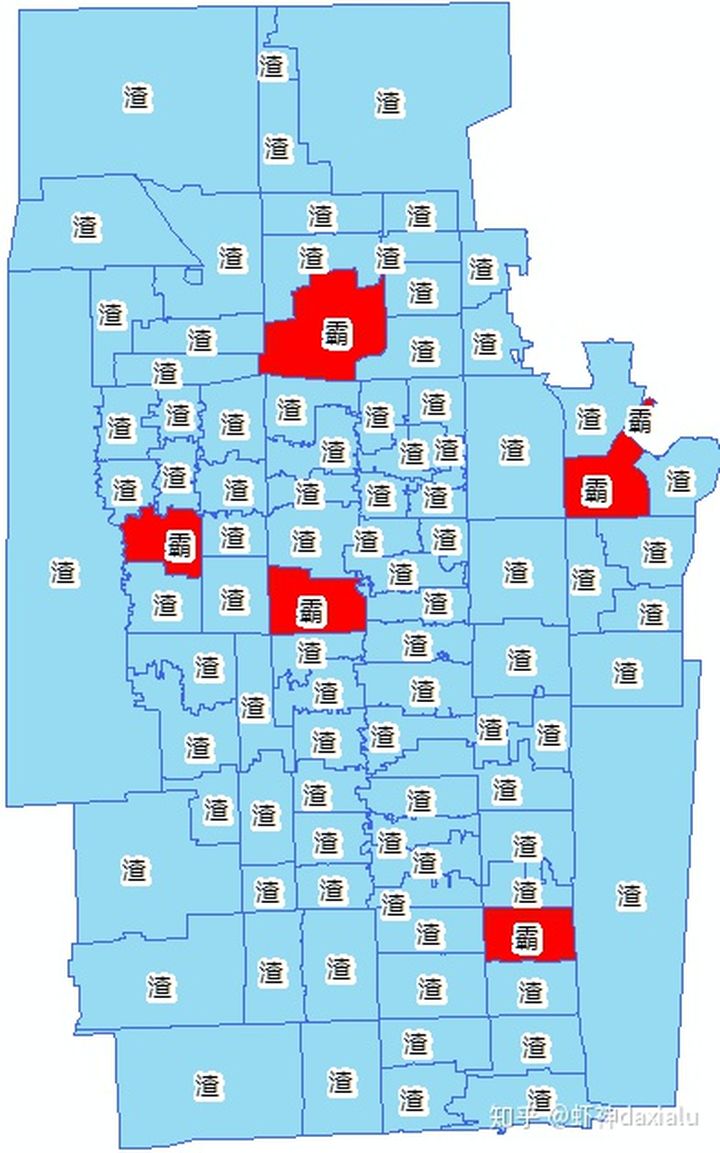
典型的大树底下不长草，所有的资源都被几个所谓的学霸区给吸取过了，实际上这也是近些年，我国的教育呈现的趋势，好的学校，到处去挖人（挖学生，挖老师）导致强者越强，而弱者越弱。

老子在几千年前就说过：天之道损有余而补不足。人道则不然，损不足，奉有余。资源、机会这种东西，最自然完美的实际上就是所谓的随机，大家机会均等，如天道一般，损有余，以补不足。但是现实中，也恰恰印证了人道的发展，损不足，奉有余。

所以理想中政府的一个重要职责，就是调节社会资源，所谓：天心不足，我心补之。

CSDN的被爬虫专用声明：虾神原创，公众号\\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。