新版白话空间统计（21）平均最近邻

Posted 2022-12-02 虾神说D

前面的章节里面，我们看了很多关于空间分布模式的基本原理，从这一章节开始，我们讲一些具体的工具和算法的使用。

前面我们用莫兰指数、P值、Z得分啥的，可以得出一份数据是属于离散、随机还是聚集，并且通过各种指数，得出聚集或者离散的程度，这种指数就是我们在定量分析时候经常用手段之一。

像莫兰指数这样的分析，在关注空间关系的同时，还要考虑属性，也就是并非单纯的在考虑空间上的聚集。而上篇文章我们说到，点数据分析里面，很多分析，并不需要（或者没有）数值型的属性，而仅仅考虑从空间位置上做分析。比如：纯粹的空间位置的数据聚集。

说到关于聚集，或者聚类，大家经常在网上看到这样的可视化：

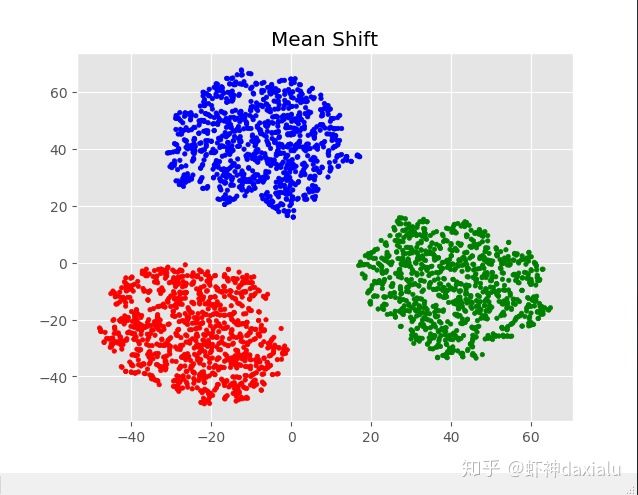
从上面可视化效果可以看到，一般只能表达XY两个属性维度，比如下面是全国各城市的气温，如果用温度进行聚类，是这个样子，可以很明显看见中国的气候分布，比如长江南北、关内关外，天山南北麓——

但是，如果我用空间数据的空间位置作为聚类属性，那么就会变成这个样子——好像也蛮标准的：东北、华北、东南、华南、西北……

但是这种聚类方式，不叫做“空间聚类”，用的是空间维度为特征进行的属性聚类，实际上应该叫做“空间要素属性化”，是属于属性聚类的一种。至于啥叫空间聚类，先挖一坑，我们在后面的分析中会详细说明。

请大家把“挖坑小能手”打在弹幕上

跑题的内容先到这里，回到我们今天的内容。

前面说到，在很多情况下，我们的分析并不一定要用到属性信息，比如这样的一种分析：

在城市中，有各类POI的分布情况都不一致，比如下面这两份数据：

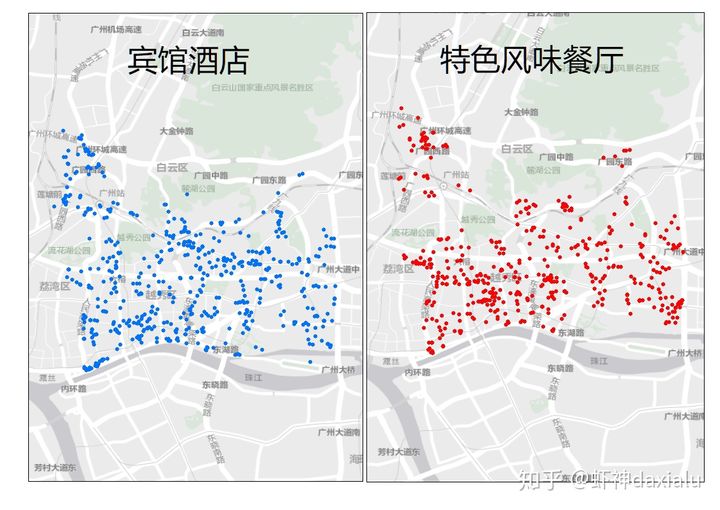
左边是广州市越秀区所有的宾馆酒店，右边是越秀区所有的特色风味餐厅。二者的数据量都差不多，宾馆酒店的数量是589，而特色风味餐厅的数量是505。

如果我们要比较两个行业之间的竞争谁更激烈的，那么能不能简单的比较单位密度呢？在越秀区整个区域的面积不变的情况下，酒店数量大于餐厅数量，论密度的话，肯定是酒店的密度更大，是不是就说明酒店的竞争更激烈呢？

一份数据，数量相同的情况下，分布情况会决定他们的关系，如下所示：

所以并不一定能够单纯的通过数量来决定他们的关系，否则就变成这个样子了：

不过，如果总数不变的情况下，理论上肯定是这样的：例如在同一个班，语文的总成绩比数学的总成绩要高出一截的话，那么参加考试人数相同的情况下，确实可以得出“相较于数学，这个班学生的语文能力较强”这一结论。

那么在空间上看，这个总数不变，通常是指我们的研究区域，所以我们可以利用下面这样一个算法：Average Nearest Neighbor（平均最近邻）。

在个算法是ArcGIS空间统计工具箱里面的一个基础工具，位置位于：

空间统计工具箱——分析模式工具集——平均最近邻

平均最近邻可以得出一份数据的具体聚集程度的指数，通过这个指数，可以对比不同数据中，哪个数据的聚集程度最大。

我们先来看看计算的方式和结果：

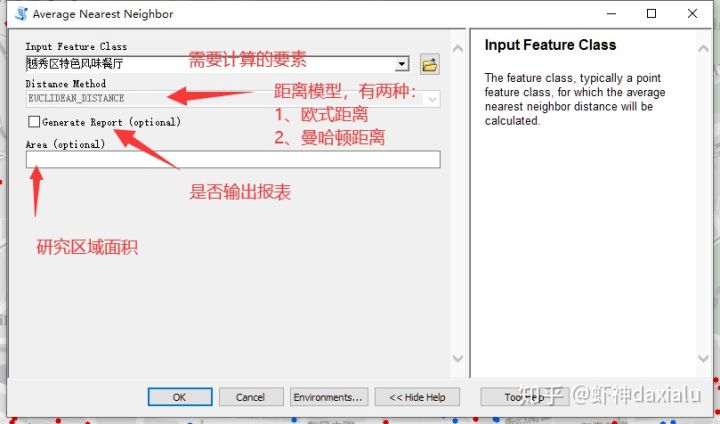
参数非常简单，只需要输入你要计算的要素就行，其他所有参数都是可选，至于第四个参数“研究区域面积”这个，我在最后面在解释。

执行结果如下：

首先是一个通用型的警告，一般来说，做空间分析，建议都要用投影坐标系来进行分析，地理坐标系都会有这个警告。

然后下面就是计算的结果了：

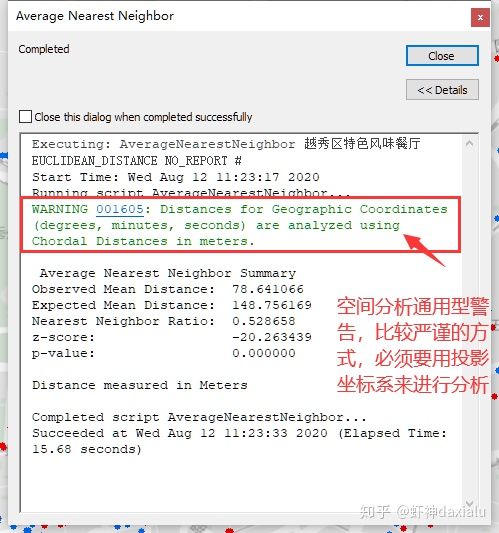
从下往上看，首先还是PZ值，这里我就不解释了，免得说浪费篇幅，大家可以回头去看以前的文章：

新版白话空间统计（10）：空间统计中的零假设

新版白话空间统计（11）：ArcGIS中的PZ值标尺

新版白话空间统计（12）：P值的表达以及空间统计上的特性

新版白话空间统计（13）：随机的力量

之后就是我们要关注的三个具体指标了：

观测平均距离（Observed Mean Distance）：每个要素的质心与其最近邻要素的质心位置之间的距离，然后计算所有这些最近邻距离的平均值。

如下所示：

计算公式：

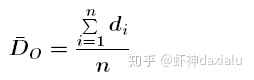
其中di 是每个要素，与他最近的要素之间的距离，如下图：

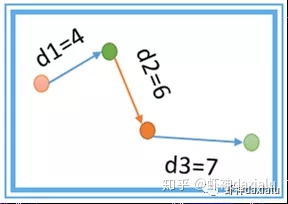
Do = (4 + 6 + 7) / 3 = 5.6667

预期平均距离：假设我们的数据，都是随机分布的，那么这些数据就应该平铺在整个研究区域中，这样平铺开来的数据预期的平均距离是。

计算公式：

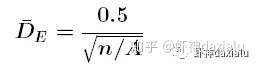
计算的方法非常简单粗暴，首先假设在研究区域内，有n个点，研究区域的面积为A，那么计算的时候就直接套用以上公式：例如，我们有3个点（这里的点，一般取使用相同数量的要素覆盖相同的总面积），研究区域的面积为60，那么

De = 0.5/sqrt(3/60) = 2.23606797749979

接下去就是这个算法里面的核心指数了——最近邻指数（Nearest Neighbor Ratio）这个指数的算法也很简单，直接用观测平均距离除以预期平均距离：

ANN = Do / De

如果观察平均距离大于预期平均距离，那么ANN > 1 ，则表示离散

反之，观测平均距离小于预期平均距离，则ANN < 1 ，则表示聚集

我们上面计算的结果约等于0.52，则表示这份数据在空间上呈现了聚集状态。

平均最近邻方法对面积值非常敏感（面积参数值的细微变化都能导致 z 得分和 p 值结果产生巨大变化）。比如下面这份数据，在不同的研究尺度下面，得到的结果也完全不一样：

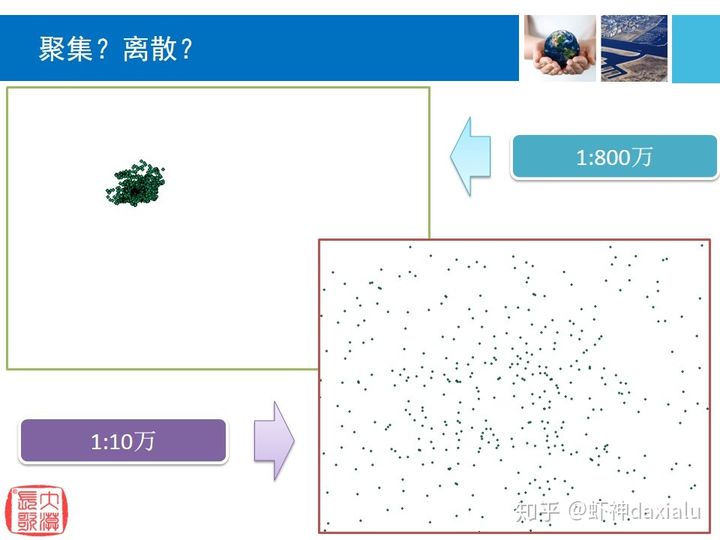
因此，平均最近邻工具最适用于对固定研究区域中不同的要素进行比较。

所以我们拉回到上面那张工具界面的图，可以看见，最后一个参数就是面积参数，这个参数可以让我们选定一个固定面积来作为标准尺度，如果你不制定面积，工具会默认使用要素的外接矩形来作为你的研究区域，例如下面的情况一。

而如果研究区域设定不一致，就有可能出现情况二，这样得到的结果就截然不同了。

最后给出这种分析方法适用的一些场景：

1、评估竞争区域或者物种领地聚集程度

我们可以用这个工具量化并比较固定研究区域中的多种植物种类或动物种类的空间分布；也可以用来比较城市中不同类型的企业的密集程度而进行竞争分析。

2、探索数据随时间变化的而发生的空间分布模式的变化

我们可以利用不同时间段的数据，来评估固定研究区域中某一种类型的企业的空间聚类中随时间变化的而发生的更改。

3、将观测到的分布信息与需要进行控制的分布信息进行比较

比如在森林砍伐以获取木材的活动中，我们可以用已经砍伐过的区域的分布，与可以进行砍伐的区域分布信息进行比较，用以确定砍伐过的区域是否比期望进行砍伐更为聚类。

这个分析工具，我们后面在做实例讲解的时候，还会不断的使用，这里就不做案例演示了。

本章打完收工，预知后事，请听下回分解。