新版白话空间统计（24）：中位数中心

Posted 2022-04-15 虾神说D

前文再续，书接上一回。（今天是个4300多字的大章，没时间的同学，看图就行）

平均数和中位数的PK也不是一两天了。

我们经常在新闻上看见统计部门发布的各种平均数，看完之后，大家的反应估计都和虾神差不多：

所有，不断有产学研三界的专家呼吁，为什么我们不用中位数，按道理来说，中位数更能反映真实情况：

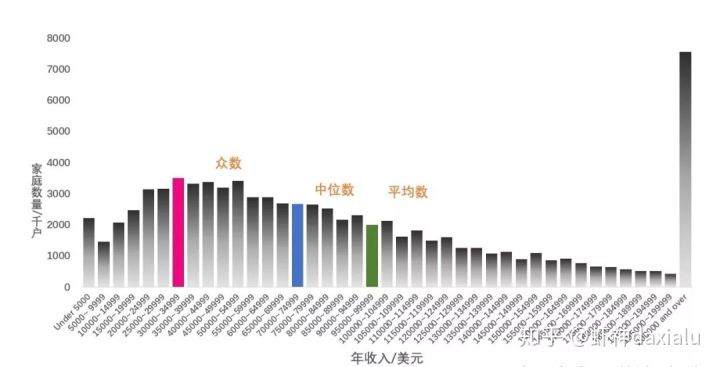
比如就是美国在国民统计中就使用了中位数。当然，美国曾经也仅运用平均数来统计来统计的，但是近几十年则越来越多地使用中位数统计。如上图所示，这是2016年美国人口普查局公布的全美家庭收入统计，我们可以看到，美国以家庭为单位的统计中，众数落在30000-34999美金的区间，中位数为7万-7万4之间，但是平均数确实最高的，到了9万5+。所以平均数这种计算方法，受到极值的影响比较大，上图所揭示的的差异，就很说明问题了：高收入的家庭会严重的拉高平均数。这个案例同时也说明，对数据群体更为完整和准确的分析，也是来自不同统计量的综合运用的。

那么我国为什么不用中位数呢？答案是：非不为也，乃不能也……

发布统计结构的中国统计部门的数据有两套口径，一套称之为：企业直报系统，也就是每个企业报告自己的在岗员工和工资总数，统计局在这套数据上直接进行计算。

但是企业不会报告每个员工的详细工资数据，所以自然也没有办法去计算中位数了：

第二套口径的数据，来自于统计局下属专设的城市调查总队，他们进行抽样入户调查。这个组织每个国家也都有，在中国，这套数据被称为“城调队数据”，理论上利用城调队数据，是可以计算出中位数来的。

那么为什么不利用城调队数据来进行计算和公布呢？答案是依然很不准确，因为我国的城调队工作依然是以工作单位为基础的，而不是以居民本身为主体的（虾神长这么大，仅遇到过一次入户调查，还是人口普查，经济普查一次也没遇到过），所以依然不行。

（以上资料参考知乎相关问题，有兴趣的同学去自行阅读）

好了，小科普到此为止，我们继续我们的空间统计学。

刚才说了中位数可以有效的避免极值影响，中位数中心也是一样，我们来看这样一张比较图：

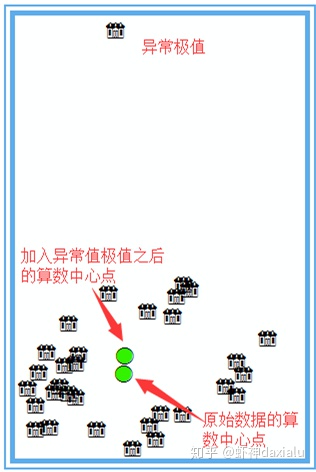
加入极值之后，算数平均值会出现明显的向极值的方向移动，然后我们再来看看中位数中心，如下：

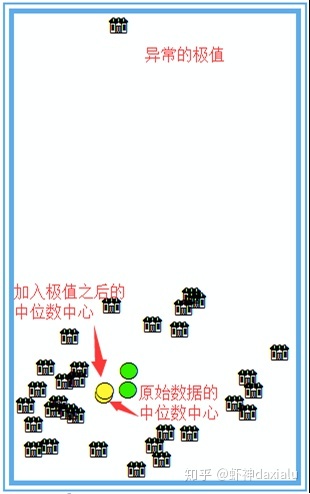
可以发现，就算加入了极值之后，中位数中心的位移没有算数平均中心位移那么大，就说明了，中位数中心，对极值（异常值）的敏感程度要低于算数平均中心。所以：中位数中心是一种对异常值反应较为稳健的中心趋势的量度。

接下去，我们来看看中位数中心的一些算法和原理。中位数中心和以前所说的中心要素很像，就是去寻找一个能够均分所有数据为两部分的数，这个数到所有的位置的距离总和最少。与此所对应的，就是平均中心未必是到所有位置距离总和最少的——中位数中心的作用更接近中心要素。

但是，中位数中心和中心要素，最大的不同点在于：中心要素计算出来的结果，必须是要素样本的中的一个原始样本；而中位数中心与平均中心都是计算出来的，可以不是原始要素中的一个，可以生成一个新的位置。

但是相对于中心要素的计算，中位数中心的计算方法就复杂很多了。

因为中位数中心没有既定的位置给你，也就是说没有起算点。如果没有起算点，那么理论上就有无数个点可以作为起算点，然后根据遍历的法则，一个个的去计算，去排序，这样系统的开销会变得无限的大。

在这里给大家讲一个小段子。

众所周知，中科院数学所是民科首要围攻的对象，每年就哥德巴赫猜想写给数学所的信，加起来能绕地球一圈……（因为民科们真的以为哥德巴赫猜想就是证明1+1，手动狗头保命）。

图：中科院数学所

先不说哥德巴赫这种高端知识，就最基础的尺规三等分角这种数学上已经证明了不可能的，也每年都有无数老大爷认为他已经可以解决了——我就遇见过一个大神，信誓旦旦说他可以三等分角，我很好奇的问他是怎么办到的时候（数学上已经证明不可能了），他掏出了一个量角器——

我当时就是差点口吐白沫……尺规作图只能使用无刻度的直尺和圆规，如果放宽条件，哪怕只是允许在直尺上做个标记(即二刻尺)，也都可以做出三等分角来，but那个不叫尺规作图……

当我把无刻度的尺规这个条件说出来的时候，大神用看白痴的眼神看着我说：现在科技进步了，可以使用了……

（PS：使用测量器具是个工程问题，不是数学问题了）

言归正传：

要说中位数中心就得先说说所谓的费马点（Fermat Point)的问题。费马点是17世纪的一个法国律师皮耶·德·费马（Pierre de Fermat，如下图）提出来的，这位专职律师被称为“业余数学之王”，在数学的神殿里面，有他一张王座镇压诸天……费马最后定理在中国习惯称为费马大定理，西方数学界原名“最后”的意思是：它就是诸神的黄昏——当一个个猜想都将被证实的时代来临，这将是最后一个。

费马点，指的是，在三角形内部，有一个点，这个点到三角形三个顶点的距离之和最短，如下图：

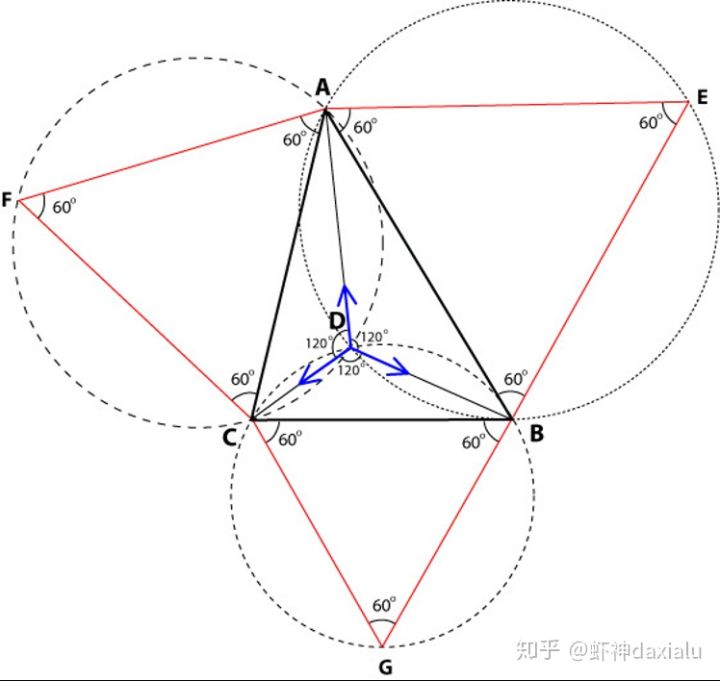
如果三角形的三个内角都小于120度，如上图：三角形ABC内部的一个点D，就是离这个三角形三个顶点距离总和最近的一个点，从这个点向三角形三个顶点连线，得出的三个角正好整分费马点所在的周角，即均为120度。所以费马点也称为三角形的等角中心。

那么如果三角形有一个内角大于等于120度，那么这个钝角的顶点就是费马点。

要找到这个费马点，不需要我们去迭代和测量（数学是一种追求完美的学科），只需要将三角形的三条边都做一个等边三角形，然后用这个等边三角形做一个外接圆，三个外接圆的交点，正好就是这个费马点。（等边三角形做外接圆的方法就不详说了，太简单了）——标准的尺规作图。

四边形的费马点就更容易了，凸四边形，费马点就是对角线交点；凹四边形，费马点就是凹点。

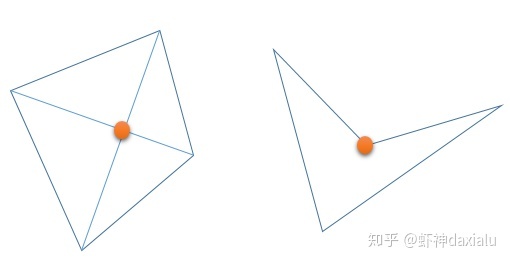
我们知道，三角形和四边形这种在数学上非常特殊的情况，在现实生活在确实不多，特别是在多点之间计算费马点的话。

所以复杂多边形内的费马点计算，也一直都是数学界津津乐道的话题。

因为复杂多边形内的费马点没有公式来实现，所以到现在为止想通过一个公式就计算出费马点是不可能的事情。当然，初等数论里面，对正多边形提出了一些方法，例如分割成多个三角形这种方法，但是仅适用于正多边形。

而且费马点的寻找是不涉及到任何权重的，所以算出来的结果是完全几何结果，几何图形的费马点完全是在图形内部。

中位数中心，实际上就是一种费马点的延伸：韦伯问题。

韦伯问题描述如下：地理上有若干个点，现在需要寻找一个到所有点距离总和最小的点，是几何学和区域学研究中的一个非常重要和著名的问题，但是最早由一个经济学家阿尔弗雷德·韦伯（德语：Alfred Weber，1868年6月30日－1958年5月2日，如下图）提出，所以也称之为“韦伯问题（The Weber problem）”。这位韦伯先生并非是一个数学家，而是一位经济学家、社会学家和文化理论家。阿尔弗雷德·韦伯是马克斯·韦伯（组织理论之父）的弟弟。他创立了工业区位理论，深刻影响了现代经济地理学的发展。

韦伯问题就是在费马点的基础上扩展了权重概念，那么带来的一个问题就是：有些点的权重，被设置为了负数，结果就是加权计算的时候，会让这个中位数中心可能跳出几何范围之外。

例如：还是仓库运输的问题，我们要计算中位数中心，那么如果有一个仓库不但可以存放中转货物，还提供了加油、修车、保养、司机休息的服务……那么这个仓库的权重计算可能就会被设置为负数，哪怕他的距离可能很大，但是所有来到这个仓库的车辆，都会直接忽略距离因素而达到更优化的效果。

不过这个世界算有一群很聪（bian）明（tai）的天才，他们有个共同的名字，叫做数学家——时代变化了之后，还有一批更聪明的天才，叫做计算机学家……在1962年，美国著名数学家，普林斯顿大学的哈罗德.威廉.库恩（一位天才的数学家和计算机理论学家，曾经获得1980年的约翰·冯·诺依曼理论奖）和罗伯特.E.库伦（Kuhn, H. W., and R. E. Kuenne） 两位首次提出一种计算方法。

这个算法说起来还是比较容易理解的，就是寻找一个候选中位数中心，然后对其进行优化，直到其表示的位置距数据集中的所有要素（或所有加权要素）的距离最小。

我们简单看看这种迭代最小二乘法解决韦伯问题的方案。具体的算法如下：

首先确定起算点，起算点的确定非常简单，Kuhn和Kuenne选择了最简单的一种起算方法，就是几何平均数，用所有点的平均中心作为起算点。

接下去就是确定迭代优化方案了。迭代的优化方案主要就是对候选点的选择，有如下几个关键：

1、以起算点为参照，在什么地方选择候选点（方向）。

2、候选点选在起算点多远的地方比较好（距离）。

先讲方向的问题，理论上来说，只需要向任意一个不同的方向移动，就可以了。随便向任意方向移动，都会产生不同的距离总和。

生成新的距离总和之后，与原来的起算点的距离总和进行对比，如果大于原来的距离总和，就说明这个候选点是错误的，丢弃，重新寻找。如果小于原来的距离总和，说明比起算点要优化，将他设为新的起算点，也就是候选点，然后以这个新的起算点，迭代进行选择寻找。

然后再讲讲移动多少距离合适。

Kuhn和Kuenne在他们的论文里面，设定了一种很实用的距离公式，就是所谓的Weiszfeld 算法，这是一种重复加权最小二乘法，如下所示：

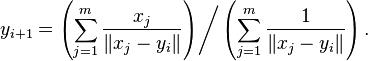
第一次选择候选点的距离的时候，直接采用所有的点的平均距离y作为移动距离，移动完成之后计算，并且把这个y带入到公式中，求解出下一次需要移动的距离。

根据我们迭代的次数的增加，会发现数据会逐渐的收敛。最后可以计算出最优的候选点，作为最后的位置。

当然，如果有权重的话，在每个点上面，还需要加上权重进行计算，如下公式：

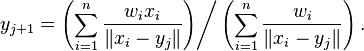
其中Wi就是每个点的权重。

理论上，这个优化可以无限的接近无穷大（与最优点的距离无限接近于0），但是无论是计算结果还是计算机能表示的结果，都是有一个极限的，在实际的计算中，这个极限就是我们可以接受的精度。

来来来，再优化这么一点点，一点点就行

一般来说，在GIS里面，就是你创建坐标系和要素图层的时候指定的精度，就是默认接受的精度值。

1996年，被美国纽约吉尔福德学院地理学家詹姆斯.E.伯特和杰拉尔德.M.巴伯(Burt, J. E., and G. Barber.)总结归纳，得出了一种优化算法。

这个算法的具体描述，请参考书籍：《Burt, J. E., and G. Barber. (1996).Elementary statistics for geographers.Guilford, New York.》

当然，里面还有很多很多其他的东西，比如各种条件什么的，我这里就不一一说明了，有兴趣的同学，请参考如下文章：

https://en.wikipedia.org/wiki/Geometric_median

https://en.wikipedia.org/wiki/Weber_problem

最后，我们来聊聊中位数中心的适用范围：比如我们需要一个对于空间异常值反应比较稳健的中心趋势的量度值，就可以考虑使用中位数中心。

就像计算火灾发生位置的研究中，我们不希望少数外围火灾使得实际的中心位置远离火灾核心区这样的一种场景，就可以使用ArcGIS提供的工具计算火灾区的“中位数中心”。

平均中心和中位数中心，都是空间统计中经常用到的工具，它们在研究某一时间的位置运动时候有广泛的应用。

例如：在犯罪分析的研究中，犯罪事件的位置可能遍布整个城区，我们就可以按照不同的时间，对其中一个区间内的数据进行中心点提取，这样就可以有效的了解，整个犯罪事件的位置是否发生趋势性的转移。

或者在对动物迁徙的研究中，可以计算某个区域若干年内的动物（如麋鹿）观测值的平均中心，来确定在不同时间段内，麋鹿会在何处聚集，从而为游客或者研究人员提供更好的信息。

具体的案例，我们以后有空在进行演示：

（请大家把挖坑小能手打在弹幕上……）