新版白话空间统计：空间自相关

Posted 2022-06-21 虾神说D

CSDN的被爬虫专用声明：虾神原创，公众号\\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。

空间自相关是学习空间统计学课程中的第一个拦路虎，据虾神所知，很多初学空间统计学的同学，在遇上这个词汇的时候，就准备放弃这一门本来可以很有意思的课程了。因为大家发现“空间自相关”这五个字，无论是拆开来，还是任意自由组合，都是认识且了解的，but……五个字合起来之后，就不明觉厉了。

那么什么叫做空间自相关呢？实际上要从我们能看懂的相关性分析说起，实际上空间自相关也是来源于单变量统计分析里面的相关性概念。

啥叫相关性分析呢？相关性就是用于衡量两组变量之间的紧密程度。比如下面这两组数据：

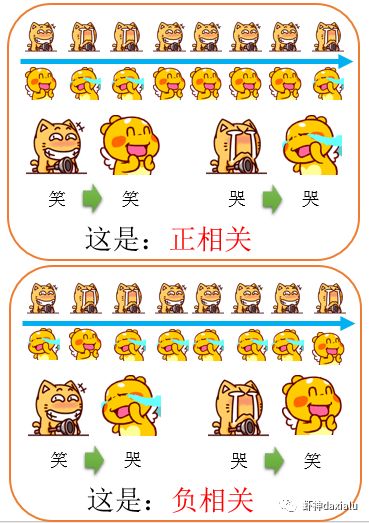
如果把上面的哭和笑，用数值进行表达，用一个数学公式就可以算出来，具体的计算公式我就不去亮了，有兴趣的同学自己去查。

通过数学公式，可以计算出这个相关系数，相关系数的值一般都在【-1,1】之间，情况如下：

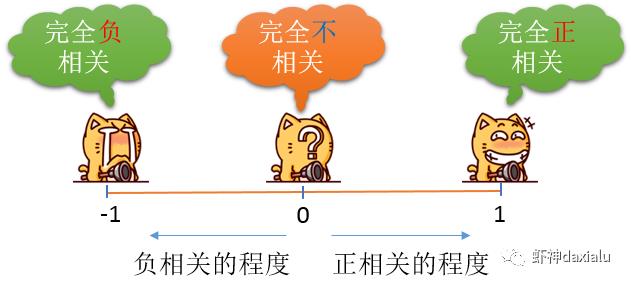
但是自相关又是啥意思呢？最早自相关来自于时间序列分析——通常时间序列分析里面的数据，除去时序维度之外，只有一个属性维度，比如全天的气温：

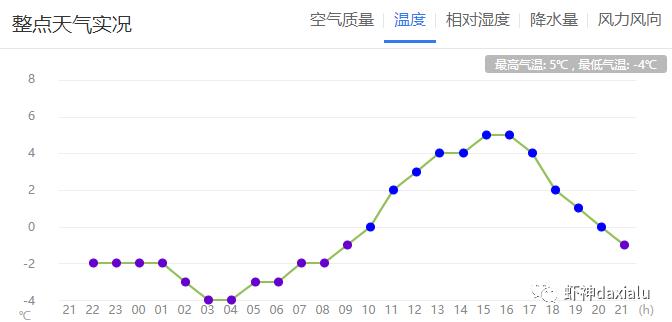
或者是原油期货数据：

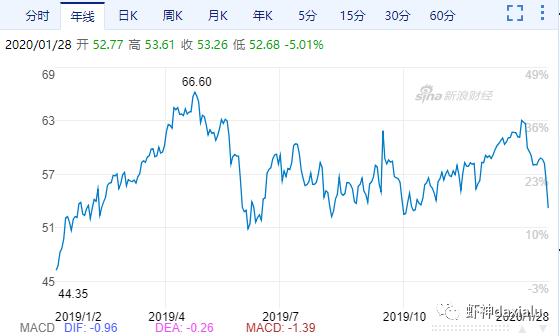
这种针对这种同一属性之间进行分析相关性的，就叫做“自相关”。

有同学看到这里，可能会问，两组数据之间进行相关分析我们很好理解，同一组数据，怎么做相关分析？难道是要把数据——

好吧，你虽然没有完全猜对，但是也差不多了——自相关分析的方法，就是用同样大小的窗口，把数据切分成若干块，比如如果仅分成两块的话：

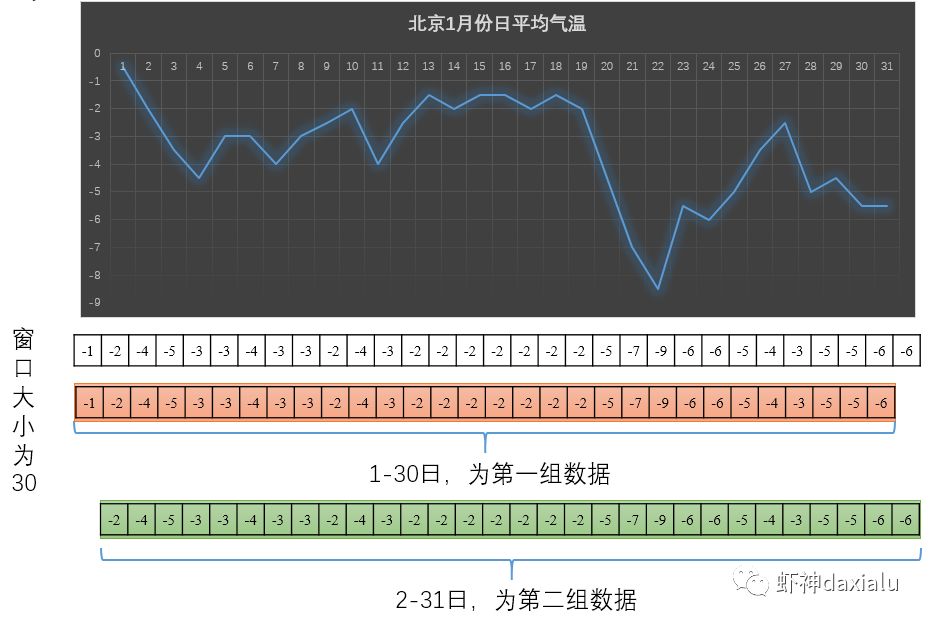
而如果分的更细，我们就可以得到若干个延时为1的序列，这些序列之间相关系数就可以很轻易的算出来了，当然，其中会有各种各样的数学公式和原理，我会（有可能的话）在另外的——黑话空间统计算法篇里面给有数学爱好的同学慢慢解释。

那么得到这一系列的延时相关系数，就是时序分析里面很重要的“自相关图”——好吧，跑题了，不过这里大家记住，自相关的“自”的含义，就是单一属性之间自行比较就好。

这种有序列的单一属性，我们很容易发现一个问题，有些序列，天然具有相关性——比如气温，一个较低的气温，前后往往跟随着的是同样比较低的气温……很少有气温突然剧烈来回变化的。

而有些序列则不然，比如上面用的原油期货数据，变化之间几乎没有规律——这种不具备相关性的序列数据，就是所谓的随机模式的数据。

不过这种分析，仅适用于时间序列这种有明确前后相邻的单一序列数据上面，最初被认为很难移植到空间上，因为空间上没有明确的可以遵循的单一顺序——所以需要一种特殊的符合地理空间规则的建模方法，使之适用于广义的空间分析上面。

所以空间自相关应运而生——那么这个空间自相关又是啥意思呢？我们先来看这样一个例子：

时间：课间操。

地点：学校操场。

当广播响起来的时候，所有学生都一路狂奔冲向操场（迟到要挨罚的），所以，如果我是校长，在楼上，看见的应该是这样的一个场面：

怎是一个乱字了得，那么这就是所谓的“随机分布”，代表了谁也不知道，哪个学生是哪个班的，哪个学生会出现在哪个位置之上，更别说想弄明白哪个学生与哪个学生之间的关系了。

划重点：随机分布代表无法预测，所有的位置概率都是均等的。

随着体育老师的口令，慢慢得变成了下面这个场面：

学生整整齐齐的占成了队列，每个人前后左右的距离都是一样，这个就是所谓的“均匀分布”，在这种均匀分布的情况下，照样没办法看出学生之间的关系。

画重点：在数据分析种，均匀分布与随机分布具有相同的含义。

5分钟后，广播体操结束，同样随着体育老师的一声口令，解散，学生们就变成了下面这个样子：

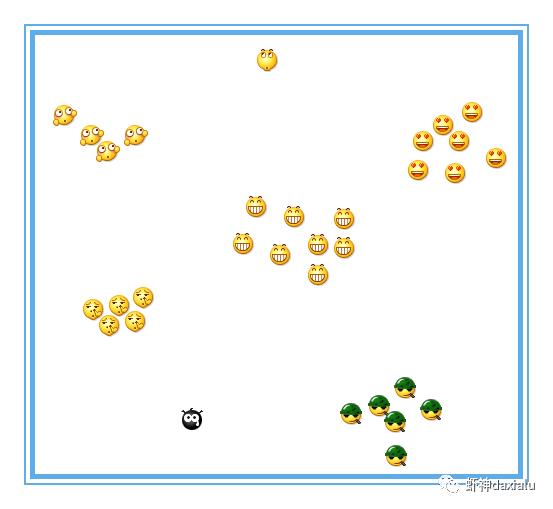
OK，作为校长的我，现在就很明显的看出，不同的学生，自己就组成了自己的一个个小团体，这就是所谓的聚类。

那么作为校长，自然会在脑中脑补，为什么这几个学生会自然的聚在一起呢？肯定是共同的爱好或者共同的目的，至于这个团体，有哪些共同的爱好和共同目的，就是学生之间的某种特征了，比如中间那一波，是喜欢打篮球的，右边那批，是什么王者农药战队的，当然右上左下，还有两个单身狗……。

这种，每个学生，与他周围的学生之间，一般有一些共有的某种特征。理论上，如果有一个带有这种特征的学生出现在操场上，那么他身边出现的，就有很大可能与他有同样的特征，而且他们之间会产生潜在的依赖性。比如喜欢打球的学生，一个人肯定没办法打，所以自然需要有共同爱好的小伙伴在旁边。

这种潜在的（因为没有很明显的表现出来，所以肯定是潜在的）的相互依赖性，就是所谓的“空间自相关”。

对空间自相关的研究，是揭示空间数据分布的一个很重要的概念，而对空间自相关中的关联性程度的计算，就是研究空间自相关的主要方法了。

那么，下一期，我们来聊聊衡量空间自相关的表现形式：空间分布模式之聚集、离散与随机。

CSDN的被爬虫专用声明：虾神原创，公众号\\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。