新版白话空间统计（22）：中心要素

Posted 2022-06-21 虾神说D

CSDN的被爬虫专用声明：虾神原创，公众号\\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。

美国著名统计学家，统计学史专家，芝加哥大学统计学院教授Stephen M. Stigler（斯蒂芬.斯蒂格勒）出过一本影响深远的著作：《统计学七支柱》，对统计学历史上里程碑式的几种统计思想的历史来源的回溯，记录的是数百年来这些思想萌芽和发展的若干瞬间。有些思想的发展或许并不瞩目，但源远流长。

何为支柱？支柱的概念就是一旦出问题，整个体系就会轰然崩塌。在Stigler教授的著作中，把统计学七支柱描述为：

其中，第一个支柱，就是所谓的聚合（Aggregation）

聚合，或者翻译成汇总也可以，是统计学赖以存在的经典用途。最原始的统计需求就是对客观世界的抽象，跟农业最相关的天文观察要求所有测量要准确，但问题是每次测出来都会有差异，那么就需要一个方法来描述相似但不一样的测量值，这就是统计聚合思想的来源。任何分析都是无法将所有的细节都完整记录的，如果人类记住一切的细节，那么庞大的信息量会让大脑直接宕机，此时抽象的意义就很大了。就好比现在很火的大数据，细节丰富但需要有意识地抽象，不然就是一堆数字的堆砌。这里最常见的统计学术语就是众数、中位数还有均值，都是聚合抽象描述的体现。

其实这个思想提出时也是被批判的，因为平均这个概念经常会导致各种问题，而聚合出来的东西例如平均人不是客观存在的，也就没法指导具体事物的描述。但本来聚合描述的就不是具体事物，它用总结替代完整描述，通过选择性舍弃一部分信息来获得更有价值的信息，这可以说是统计学的一个根基。

在统计学上，有这样一个著名的公案：

一位舰长计划夺取敌人的一座要塞，他派了两名间谍潜入要塞，并要求其返回报告要塞中加农炮的口径，如此就可以准备尺寸合适的加农炮弹，以确保夺取要塞后可以加强防守。一名间谍报告口径是8英寸，另一名报告是9英寸。

那么舰长应该配置8.5英寸的加农炮弹吗？当然不会，无论哪种情况，这个炮弹都不能用。哪怕扔硬币决定取两种尺寸中的某一种，都好过注定失败的平均值。

同样，在空间统计中，也有很多这样的具有代表性的概念，比如今天我们要说“中心要素”。

在经典统计学中，中位数表示从它开始，可以将整份数据分成上下两个部分，关键是这个数不能是被计算出来的，而是数据中的一个样本（当然，如果是偶数个，那么是中间两个样本的平均值）。

那么如果是空间数据，比如一堆点，那么我们怎么去选择它们的中心要素呢？

经典统计学中，对一组数据进行排序之后寻找中位数，往往都是一维的，也就是排列成了一条直线队列，这样很容易找到中位数。

但是在空间分析中，哪怕是点状要素，也是平面二维分布的，那么如果让你对二维平面的数据线进行一个排列，那么按照你的想法，如何进行？以X坐标为准，Y坐标为第二顺位？还是以Y坐标为准，X为第二顺位？南向北排列，还是北向南？所以在二维平面上进行排列，本来就是不靠谱的事情。

所以在空间上，中心要素的计算方法，用的是距离：

首先，用点与其他每个点的距离之和，来作为该点的值，如下：

A点的距离总和 = 7 + 9 + 4 + 7 + 7 + 3 = 37

B点的距离总和 = 3 + 4 + 3 + 6 + 6 + 3 = 25

以此类推，把所有点的距离总和都计算出来，然后进行排序，最后选取距离总和最小的那个点，就是所谓的中心要素。

距离计算的方式，ArcGIS提供了两种，分布是欧式距离和曼哈顿距离，当然，你如果已经明白了这个工具的算法，自己去写代码实现也是可以的。

这个算法有啥用呢？

首先，我们先来理解一下何为“中心”，我们经常说的，“我们紧密团结在以为中心的周围”，这样我们通常把中心当成了“最重要”的意思。

实际上中心代表并不是最重要的，中国自古以来讲究“中庸”，讲究的就是“不偏不倚、无过无不及”，所谓的中心，指的是最平衡的一个点，是从他这个位置，到任何一个其他的位置，总体距离是最短的。

所以古代宰相的主要功能，就叫做“调和阴阳”，站着一个不偏不倚的位置上，对各方势力进行平衡。

所以，找到中心，就等于找到了一个全局最优的点。

下面我们来看一个简单的例子：

这里面的每一个房子代表是城内的一个仓库，现在有一批货物，要分发到每个仓库中去，那么我们要关心的是，如何选择最少的成本，也就是最短的运输路径来完成。

如果按照传统的思想，我当然找到一个中心点，这个中心点离所有的仓库的距离总和是最少的，这样当然是最好的，但是如果这个中心点并非是一个仓库，难道为了这个中心点，我们还要新建一个仓库么？那当然是不可能的。

所以我们要从这些仓库里面，寻找到位于最中心的一个仓库，从这个仓库出发，到所有的仓库，他们的路程距离最短。

这个仓库，就是中心要素了。计算如下：

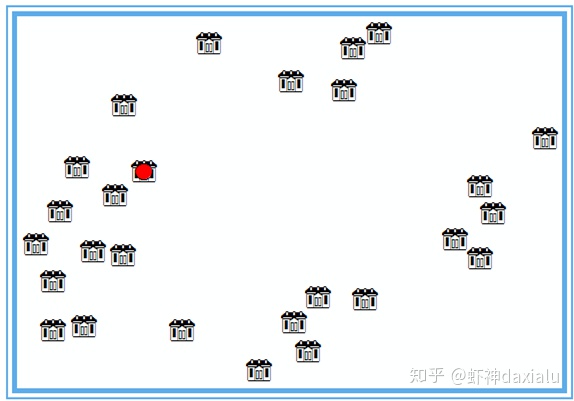
如上图，红色的这个点，就是所有仓库的中心要素了，它可能不在所有数据的中心位置，但是它是现有数据中，所有其他要素的最小累积距离相关联的要素。

当然，在ArcGIS里面，还提供了权重选项，如果选择了加权，就还可以设置其他的条件，比如考虑到仓库的承载量等。

最后总结一下空间统计里面的中心要素与经典统计里面的中位数的异同点

相同点

1、寻找到的数据，都是样本数据中的一个样本。

2、从位置上来看，中位数和中心要素都是到所有其他样本最近的一个点。

不同点：

计算方法不同。中位数是通过排序然后通过样本在序列中的位置来确定的。而中心要素是通过与所有要素的距离总和进行计算，得到距离最小的那个要素。