概率论与数理统计期末复习抱佛脚：公式总结与简单例题（完结）

Posted 2022-06-13 karshey

不全。
截图来自猴博士的视频（B站搜猴博士即可）。
我的稍微完整一些的笔记（例题具体解答在这里面）：【猴博士】概率论与数理统计 笔记总结（完结）
多图预警。

文章目录

• • 第一章：随机事件和概率
  • • 古典概型
    • 几何概型
    • 事件的概率
    • 事件的独立性
    • 条件概率
    • 全概率公式
    • 贝叶斯公式
  • 第二章：离散型随机变量
  • • 一维离散型求分布律
    • 二维离散型求分布律
    • 二维离散型求边缘分布律
    • 一维离散型求分布函数
    • 二维离散型求分布函数
    • 一维离散型求期望、方差
    • 二维离散型求期望、方差
  • 第三章：连续型随机变量
  • • 一维连续型求概率
    • 二维连续型求概率
    • 一、二维连续型：已知F,求f；已知f,求f
    • 二维连续型求边缘分布函数
    • 二维连续型求边缘密度函数
    • 已知两个边缘密度函数求f(x,y)
    • 条件概率密度函数
    • F、f的性质
    • 一维连续型求期望、方差
    • 二维连续型求期望、方差
  • 第四章：常见的分布
  • • 均匀分布 U
    • 泊松分布 P
    • 指数分布 E
    • 几何分布 Ge
    • 超几何分布 H
    • 正态分布 N
    • 二项分布 B
  • 第五章：随机变量的数字特征、极限定理
  • • 协方差、相关系数
    • 不相关、相互独立时的期望和方差
    • 中心极限定理
  • 第六章：数理统计基础
  • • 统计量相关小题
    • 三大分布的判定
    • 总体服从正态分布的统计量小题

第一章：随机事件和概率

古典概型

有放回：

无放回：

几何概型

题干类型如下：

解法：

题干中两道例题的答案：
17/25
3/4

还有两道例题：

1/Π+1/2
9/32

事件的概率

例1：

答：
0.3；

例2：

答：
5/12

事件的独立性

例1：

答：
0.2.

条件概率

$$P(M|N)=\frac{P(MN)}{P(N)}$$

分母是竖线后的概率，分子是竖线前事件和竖线后事件同时发生的概率。
含义：N发生的条件下M发生，即MN同时发生的概率除以N发生的概率。

全概率公式

像是分类讨论，各论各的

例题：

答：

例题：

解：

贝叶斯公式

题干特征：多个对象；多个对象形成一个总体；在已知总体里某事发生的情况下，求抽的东西来自某个对象的概率。

例题：

解：

第二章：离散型随机变量

一维离散型求分布律

P之和为1.

ps：分布律的其他标志：

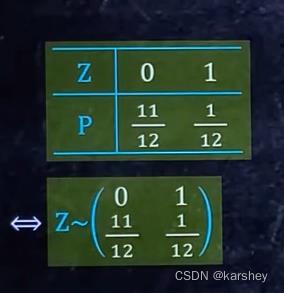
例题：

解：

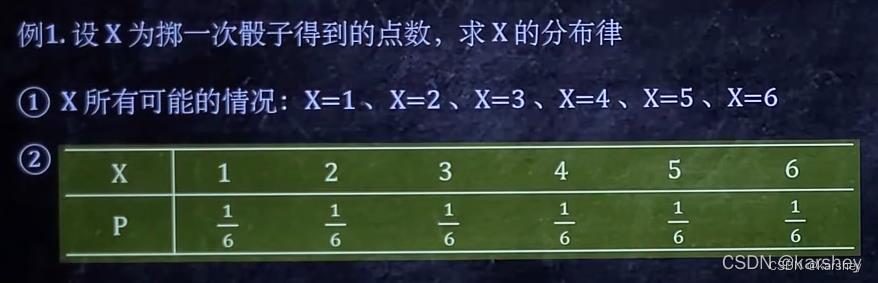
二维离散型求分布律

二维离散型求边缘分布律

什么是X、Y的边缘分布率？其实就是X、Y的分布律。

例题：

解：

一维离散型求分布函数

$$F_X(x)表示的是PX\le x$$

例题：

解：

二维离散型求分布函数

$$F(x,y)=FX\le x,Y\le y$$

什么叫做以左上角为起点，尽可能多做长方形：
若有2x2的分布律，则可以作4个长方形。
注意：左闭右开

注意：0 其他不要忘了。

一维离散型求期望、方差

二维离散型求期望、方差

做题步骤：

1. 求边缘分布率
2. 用一维的方法求

例题：

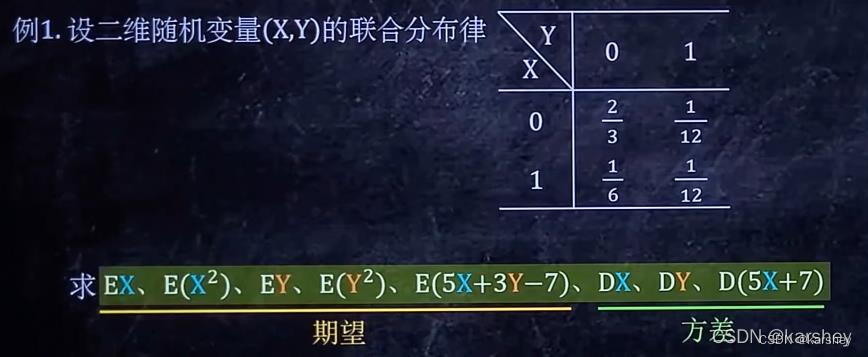
解：

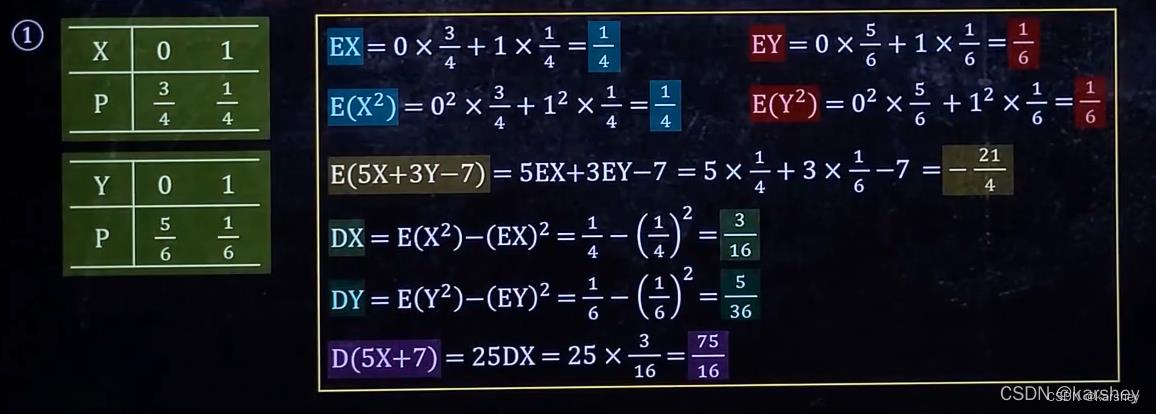
第三章：连续型随机变量

一维连续型求概率

解法：求积分。

一些补充：这三个是一个意思
$$\begin{gathered} PY\le y \\ Y的分布函数 \\ {F}_Y(y) \end{gathered}$$

例题：

例1、2：ln2.
例3：分类讨论+分部积分法。
或者把这个背下来：(-e^-x)'=e^-x

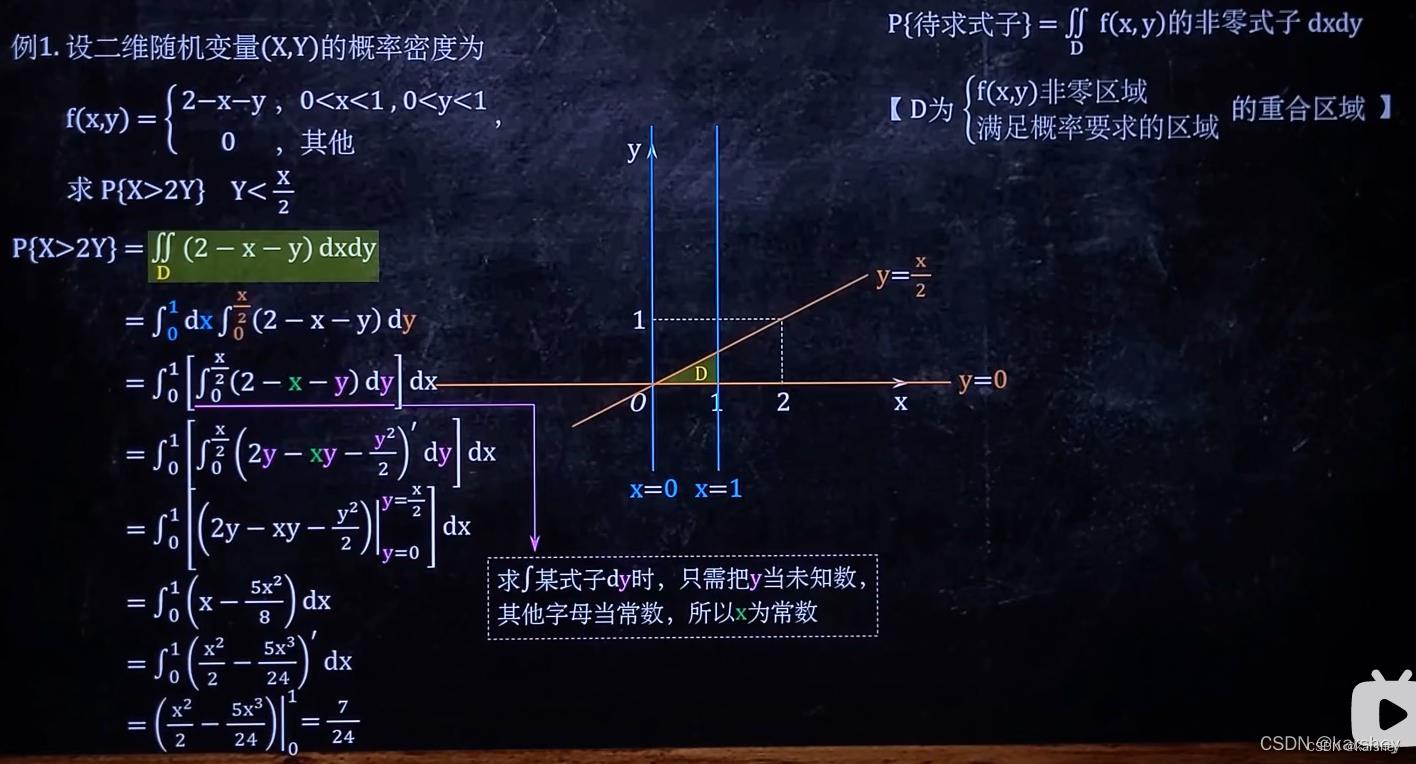
二维连续型求概率

解法：二重积分。

例题：

解：
注意范围即可。

一、二维连续型：已知F,求f；已知f,求f

啊，这个好难，我感觉不会考。
先放个完整笔记的链接：【概率论与数理统计】猴博士 笔记 p17-20 一、二维连续型：已知F,求f；已知f,求f

二维连续型求边缘分布函数

$$\begin{gathered} F_X(x)=F(x,+\infty ) \\ {F}_Y(y)=F(+\infty ,y) \end{gathered}$$

代入即可。

例题：

解：

二维连续型求边缘密度函数

$$\begin{gathered} f_X(x)={\int }_{-\infty }^{+\infty }f(x,y)dy \\ {f}_Y(y)={\int }_{-\infty }^{+\infty }f(x,y)dx \end{gathered}$$

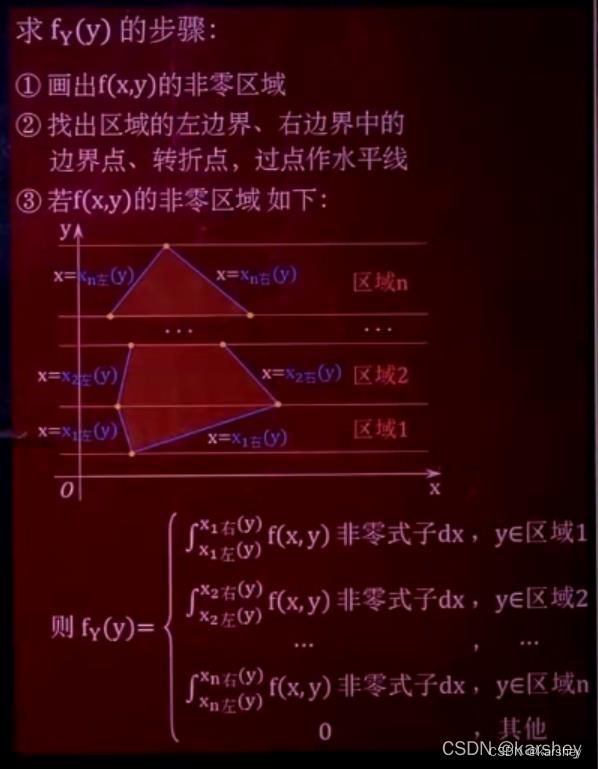
例题：

解：
例1：

例2：

已知两个边缘密度函数求f(x,y)

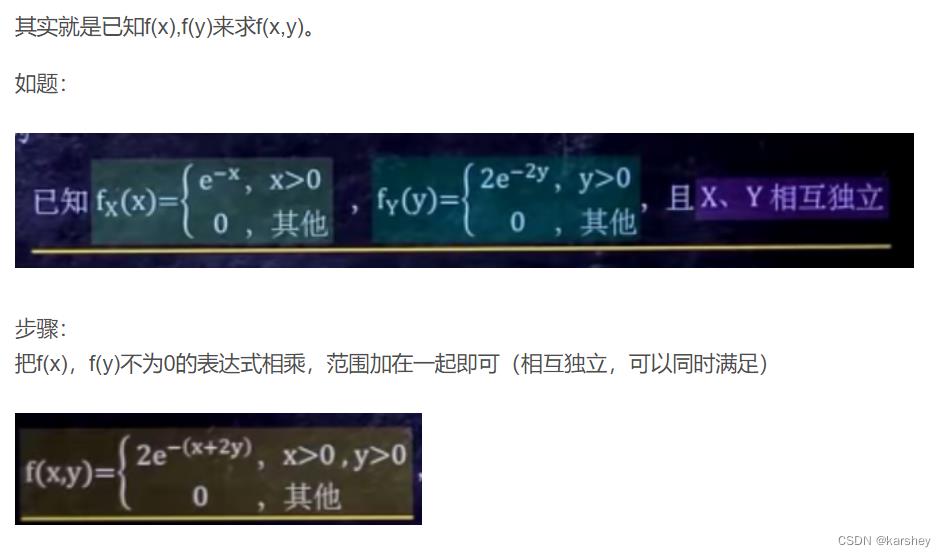
条件概率密度函数

例1：

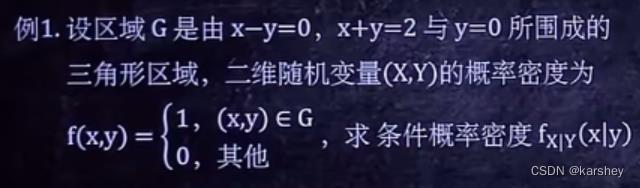
解：套公式+注意x、y范围。

例2：

解：

F、f的性质

例题：

解：

例题：

解：

一维连续型求期望、方差

例题：

解：

二维连续型求期望、方差

有两种做法：
方法一是把二维降成一维，然后用上节课的方法做。
本节主要用方法二：求什么就乘什么，然后求其总体的二重积分。

第四章：常见的分布

均匀分布 U

泊松分布 P

指数分布 E

$$\begin{gathered} PX已经怎样后，还能继续怎样=PX还能怎样 \\ 即P已经A，还想B=PB \end{gathered}$$

几何分布 Ge

超几何分布 H

超几何分布感觉举例子更好理解：

正态分布 N

关于正态分布的很多例题详见链接：【概率论与数理统计】猴博士 笔记 p33-35 超几何分布、正态分布、二项分布,这里就只放一些典型的。

例题：

解：

例题：

解：

二项分布 B

例题：

解：

第五章：随机变量的数字特征、极限定理

协方差、相关系数

计算相关的例题详见：【概率论与数理统计】猴博士 笔记 p36-37 协方差、相关系数、不相关、相互独立时的期望和方差
个人认为主要是套公式，所以记住公式就好了，可以不用做例题。

不相关、相互独立时的期望和方差

例题：

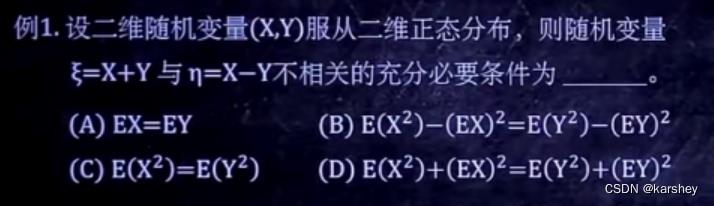
答：
B。

中心极限定理

求独立同分布的X的和。

例题：

解：
注意设变量的格式。

第六章：数理统计基础

统计量相关小题

注意，S的分母是n-1

三大分布的判定

只有三种分布：

1. X（卡方）分布——平方和
2. t分布——分母是（平方和除以n）再开根号
3. F分布：F(n,m)——分子是n个的平方和除以n，分母是m个的平方和除以m

注意，要服从标准正态分布.
若不服从，要标准化。

例题：

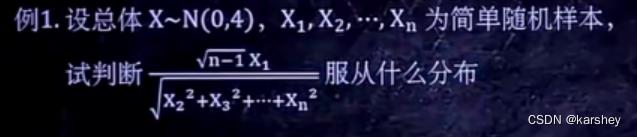
解：

例题：

解：

例题：

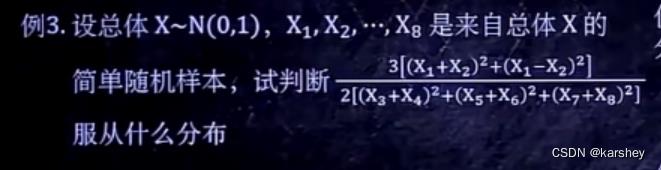
解：

总体服从正态分布的统计量小题

狂背公式：

本小节例题基本都是套公式，不赘述了，详见：【概率论与数理统计】猴博士 笔记 p41-44 统计量相关小题、三大分布的判定、性质、总体服从正态分布的统计量小题