原子公式：由谓词符号和若干项组成的谓词演算，是谓词演算基本积木块。
项包括 : 常量符号、变量符号、函数符号等。 定义原子公式为真值或假值就表示了某种 语义 (semantics) 。若 t 1 , t 2 , …, t n 是项， P 是谓词，则称 P(t 1 ,t 2 ,…,t n ) 为 原子谓词公式（原子公 式）。 无变量 的原子公式取值确定， 包含变量 的原子公式取值不定。 举例： “机器人（ ROBOT ）在 1 号房间（ room1 ）内”  INROOM （ ROBOT ， room1 ）为真  INROOM （ ROBOT ， room2 ）为假

连词和量词

1. 与、合取（conjunction)：用连词∧把几个公式连接起来而构成的公式。
合取项是合取式的每个组成部分。
例：LIKE(I，MUSIC)∧LIKE(I，PAINTING)
（我喜爱音乐和绘画。）
2. 或、析取（disjunction）：用连词∨把几个公式连接起来而构成的公式。
析取项是析取式的每个组成部。
例：PLAYS(LILI，BASKETBALL)∨PLAYS(LILI，FOOTBALL)
（李力打篮球或踢足球。）
3. 蕴涵（Implication）:“→”表示“如果—那么”（IF—THEN）关系，其所构成的公式叫做蕴涵。
4. 非（Not）表示否定，¬、～均可表示

连词的优先级：
¬, ∧, ∨ (, ) , →, ↔

合式公式的真值表

等价关系

等价(Equivalence): 如果两个合式公式，无论如何解释，其真值表都是相同的，那么我们就称此两合式公式是等价的。

注意：（10）说明在一个量化的表达式中的约束变量是一类虚元，它可用任何一个不在表达式中出现过的其他变量符号来代替

永真蕴含式

置换与合一

置换定义：置换是形如t1 /x1 ,t2 /x2 ,…,tn /xn 的有限集合，其中t1 ,t2 ,…,tn是项；x1 ,x2 ,…,xn 是互不相同的变元；ti /xi 表示用项ti 替换变元xi 。

要求：ti与xi 不能相同，xi 不能循环地出现在另一个ti 中。

例如：a/x, c/y, f(b)/z 是一个置换，但 g(z)/x, f(x)/z不是一个置换，原因是x和z之间出现了循环置换现象，若改为g(a)/x, f(x)/z即可

设θ=t1 /x1 ,t2 /x2 ,…,tn /xn 是一个置换，F是一个谓词公式，把公式F中出现的所有xi 换成ti(i=1,2,…,n)，得到一个新的公式G，称G为F在置换θ 下的例示，记作G=Fθ

置换的合成（了解）

合一定义：设有公式集F=F1 , F2 ,…,Fn ，若存在一个置换θ，可使 F1θ=F2θ=…=Fnθ，则称θ是F的一个合一。称F1 ,F2 ,…,Fn是可合一的。

例：

设有公式集F=P(x, y, f(y)), P(a, g(x), z)，则 λ=a/x, g(a)/y, f(g(a))/z 是它的一个合一。

一般情况下,一个公式集的合一不惟一。

最一般合一：设σ是谓词公式集F的一个合一，如果对F的任意一个合一θ都存在一个置换λ，使得 θ= σ· λ，则称σ是一个最一般(或最简单)合一

消解原理

 消解 : 对谓词演算公式进行 分解、化简，消去一些符号 , 以求得导出 子句 ，又称 归结。  消解原理 ：  (1) 一种用于 子句公式集 的重要推理规则  (2) 子句 是由文字的析取组成的公式  (3) 一个原子公式、原子公式的否定叫作 文字 注意：不含任何文字的子句称为 空子句 。由 子句、空子句 所构成的集合称为 子句集  消解过程 ：消解规则应用于 母体子句对 , 以便产生导出子句 举例： E1 ∨ E2 , ～ E2 ∨ E3 消解导出 E1 ∨ E3

归结的方法：鲁滨逊归结原理

鲁滨逊归结原理

核心：两个子句的归结式、

定义1：若P是原子谓词公式，则称P与﹁P为互补文字

定义2：设C1和C2是子句集中的任意两个子句，如果C1中的文字L1与C2中的文字L2互补，那么可从C1和C2中分别消去L1和L2，并将C1和C2中余下的部分按析取关系构成一个新的子句C12，则称这一过程为归结，称C12为C1和C2的归结式，称C1和C2为C12的亲本(父辈)子句

总结

9步法求取子句集

(1)消去蕴涵符号
(2)缩小否定符号的辖域(狄·摩根定律)
(3)变量标准化(哑元唯一)
(4)消去存在量词()
(5)化为前束形
(6)化为合取范式(∧)
(7)消去全称量词()
(8)消去连词符号(∧)
(9)更换变量名(同一变量名不出现在一个以上子句)

例题

解：

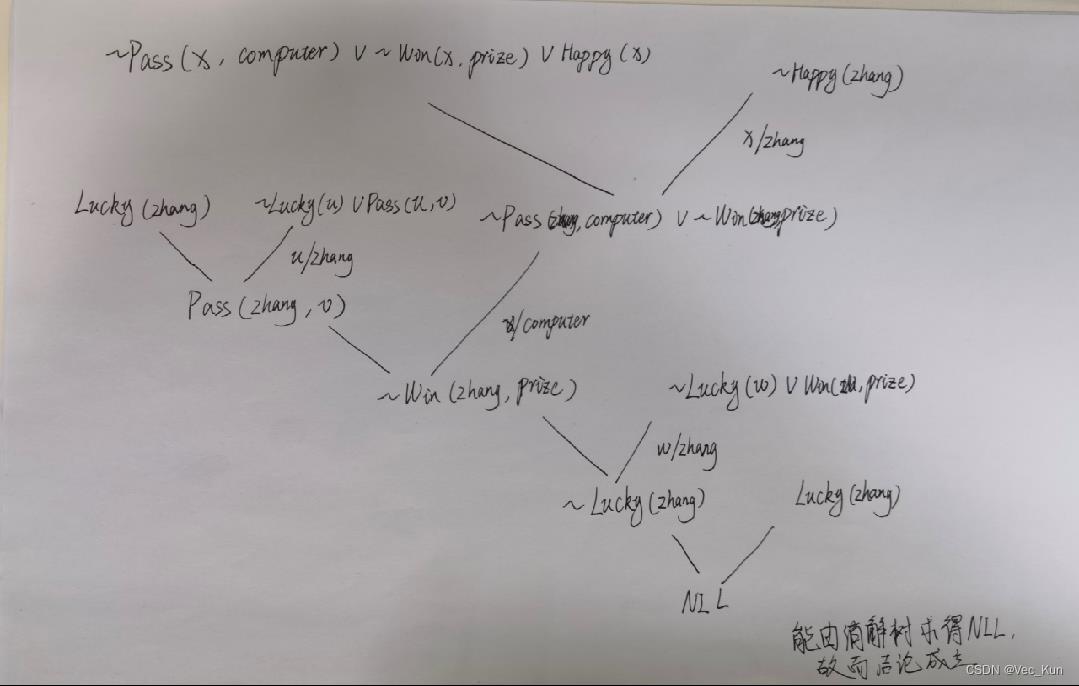
由①和⑦，用zhang置换x ~Pass(zhang, computer)∨~Win(zℎang,prize) ⑧
由③和⑤，用zhang置换u Pass(zhang, v) ⑨
由⑧和⑨，用computer置换v ~Win(zhang, prize) ⑩
由⑥和⑩，用zhang置换w ~Lucky（zhang）（11）
由⑤和11可得空子句NIL，所以结论成立，消解树如上图所示。

以上是关于电子科技大学人工智能期末复习笔记：一阶逻辑的主要内容，如果未能解决你的问题，请参考以下文章

电子科技大学人工智能期末复习笔记：MDP与强化学习

电子科技大学人工智能期末复习笔记：概率与贝叶斯网络

人工智能原理复习 | 归结原理

华南理工大学电力电子技术（王兆安）期末复习笔记2 第三章第四章