线性代数之特征值与特征向量的求法
Posted ShenLiang2025
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了线性代数之特征值与特征向量的求法相关的知识，希望对你有一定的参考价值。
线性代数之特征值与特征向量的求法
特征值与特征向量
已知如下矩阵A，求解其特征值和特征向量。
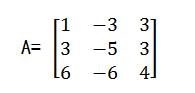
首先构造特征方程 det(λE-A)
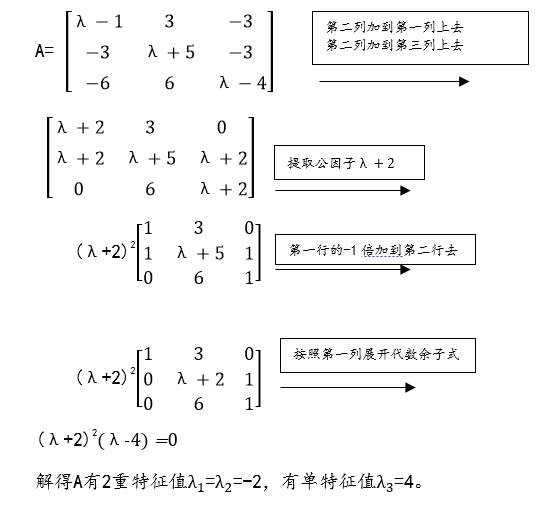
情况一:
特征值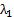
=
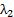=-2时解方程组(-2E-A)X=0，即得：
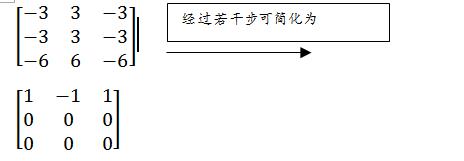
于是得同解方程组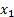 
-
+
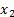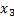=0，解为
=
-
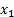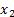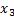(这里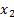
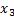, 为自由未知量)。
分别令自由未知量 =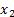 
, 
= 
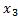进而得到基础解系为：
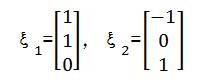
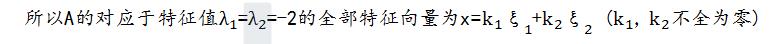
情况二：
特征值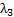
=4时解方程组(4E-A)X=0，即得
总结
Step1：先构造特征方程、展开特征多项式，求出特征值。
Step2：对得到的特征值分别带入原矩阵并化简为行简化型
Step3：求出对应行简化型对应的基础解系并通过通解表示出特征向量
以上是关于线性代数之特征值与特征向量的求法的主要内容，如果未能解决你的问题，请参考以下文章