线性代数之向量线性相关线性表示的求法
Posted ShenLiang2025
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性代数之向量线性相关线性表示的求法相关的知识,希望对你有一定的参考价值。
线性代数之线性相关线性表示的求法
线性相关
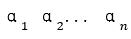 向量是n个m维(每个向量分量的个数)的向量,若存在一组不全为0的
向量是n个m维(每个向量分量的个数)的向量,若存在一组不全为0的
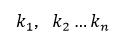 使得
使得 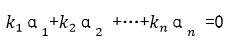 则
则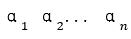 是线性相关的,反之线性无关。
是线性相关的,反之线性无关。
线性无关即等价于以下命题:
- 线性不相关
- 找不到一组不全0的
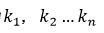 使得
使得 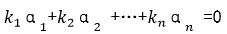
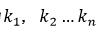 全为0
全为0
几种情况:
关于单个向量
- 向量组中两个向量成比例,则两个向量必线性相关
- 含零向量的任向量组必线性相关(取0向量的系数为1或者k,其余均为0)
- 一个零向量必线性相关
- 一个非零向量必然线性无关
- 一个向量线性相关的充要条件是向量为0向量
线性表示
如果向量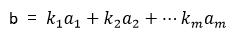 则b是向量组A的线性组合,这是向量b可有向量组A线性表示。这里其实转换为了方程有解,全是0也是有解。
则b是向量组A的线性组合,这是向量b可有向量组A线性表示。这里其实转换为了方程有解,全是0也是有解。
特别的:
- 线性表示时系数可以全是0
- 0向量可有任意向量组表示。
任何向量都可由 (1,0,...0),(0,1,0...0),(0,0,1...0) ...(0,0...0...1)表示
线性相关例子汇总
判断线性相关(不含参数)
该方法是根据矩阵的秩的定义来求,如果找到k阶子式为0,而k-1阶不为0,那么k-1即该矩阵的秩。
#Sample1(示例一),判断如下向量组是否线性相关:
1: 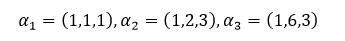
2: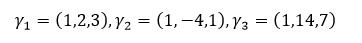
解:针对第一题:
Step1:首先我们先立方程 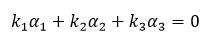
针对其解的情况来判断向量组是否线性相关(有解)或者无关(无解)。
Step2:于是我们得到下式:
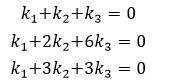
Step3: 我们对k的行列式化简得到如下行列式:
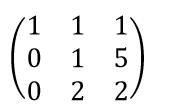
该行列式不为0,所以当前关于k的方程组有唯一解,即
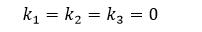 所以当前向量组里的向量
所以当前向量组里的向量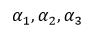 线性无关。
线性无关。
针对第二题:同样的思路
Step1:设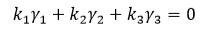
Step2:于是我们得到
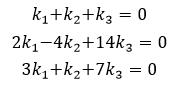
Step3:针对k化简得到如下行列式,易得其为0,所以k有非零解。
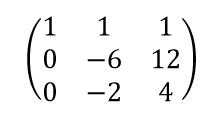
Step4:因为关于k的解有无穷个,所有这里取
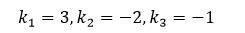
换言之存在不全为0的数使得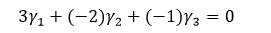 即
即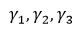 线性相关。
线性相关。
判断线性相关(含参数)
针对这种类型的问题,一般将它们按照列(行)的形式构成矩阵,对矩阵做行(列)变换,使矩阵变成阶梯型。最后根据矩阵中参数的取值是否使得其所在行(列)为零行来判断向量组的线性相关性。(参数所在行全为0则行列式为0,线性无关,否则相关)。
#Sample2(示例二):已知向量组
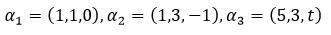 判断其相关性。
判断其相关性。
解:
Step1:因这里向量组的向量个数和向量的维数相同,所以可以按照列组成行列式。
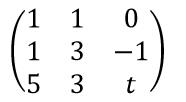
Step2:第1行的-1倍加到第2行上去,第1行的-5倍加到第3行上去,则得:
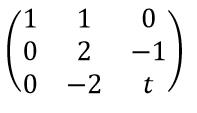
即行列式等于2(t-1)
Step3:针对Step2里的t进行讨论,如果t=1,则行列式等于0(即方程有无穷非非零解),则线性相关,如果t≠1则行列式不等于0(即方程只有零解),则线性无关。
线性表示例子汇总
阶梯法判断线性表示
利用矩阵的初等变换不改变矩阵的列的线性关系的特点求解。
#Sample3(示例三)
向量β=(4,4,1,2)是否可由如下向量组线性表示,如果可以,写出表达式。
1: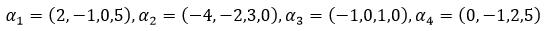
2: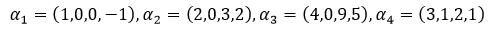
解:
针对第一题:
Step1:用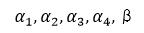 作为列向量构成矩阵A,则A为
作为列向量构成矩阵A,则A为

Step2:交换第1和第2行,则化为:

Step3:第1行的2倍加到第2行上去,第1行的5倍加到第4行上去,第1行乘-1,则最终化为:

Step4:在对step3里的矩阵化简,第3行的3倍加到第2、4行上去,则得:

Step5:在对step4里的矩阵化简,第2行的-3倍加到第3行上去,第2行的1倍加到第3行上去,则得:
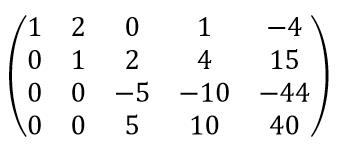
Step6:在对step5里的矩阵化简,第3行的1倍加到第4行上去,第3行除以-5,则得:

Step7:由A的阶梯型可知 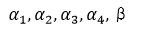 这5个向量的向量组的秩(阶梯型里非零行的行数)是4,所以该向量组的秩必定包含β,即β不能由
这5个向量的向量组的秩(阶梯型里非零行的行数)是4,所以该向量组的秩必定包含β,即β不能由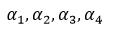 线性表示。
线性表示。
针对第二题:
类似第一题,可将构成的矩阵
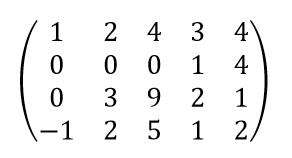
化简为:

则可见即β可由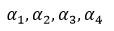 线性表示,即
线性表示,即
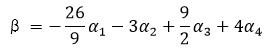
以上是关于线性代数之向量线性相关线性表示的求法的主要内容,如果未能解决你的问题,请参考以下文章