数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | 求 1 的傅里叶变换 )

Posted 2022-03-10 韩曙亮

文章目录

• 一、求 1 的傅里叶反变换
• • 0、周期 2π 的单位脉冲函数
  • 1、问题分析
  • 2、涉及公式介绍
  • 3、1 的傅里叶反变换
  • 4、1 的傅里叶反变换

一、求 1 的傅里叶反变换

---

已知 傅里叶变换

$$X(e^{j\omega })=2\pi \tilde{\delta }(\omega )$$

求该 傅里叶变换的 反变换

$$ISFT[X(e^{j\omega })]$$

0、周期 2π 的单位脉冲函数

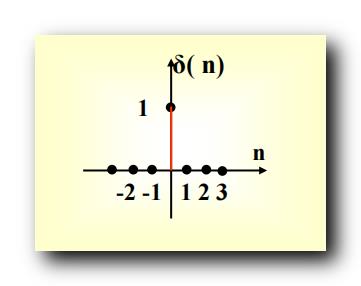
单位脉冲函数 ( 单位冲击函数 ) 对应的 函数图像 如下 : 横轴是 $n$ , 纵轴是 $\delta (n)$ ;

• $n=0$ 时 , $\delta (n)=1$
• $n=1$ 时 , $\delta (n)=0$
  

如果写成 $\tilde{\delta }(\omega )$ 样式 , 说明该 单位脉冲函数 是以 $2\pi$ 为周期的 , $\tilde{\delta }(\omega )$ 可以写成如下式子 :

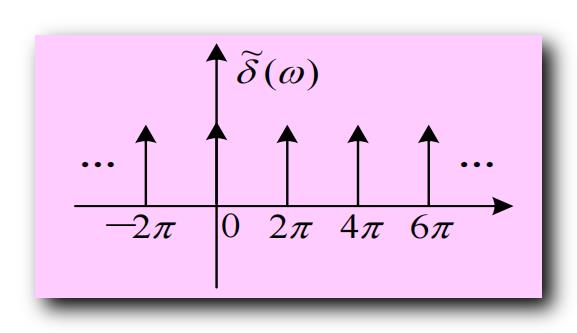
$$\tilde{\delta }(\omega )=\sum _{m=-\infty }^{\infty }\delta (\omega -2\pi m)$$

$m$ 取值 $(-\infty ,+\infty )$ ;

其函数图像如下样式 :

1、问题分析

求 1 的 傅里叶变换 SFT , 无法直接求出 , 这里求其 傅里叶反变换 ;

$\tilde{\delta }(\omega )$ 序列如下图所示 :

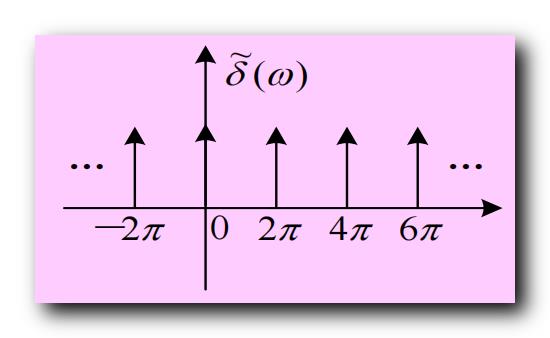
除了在 $0$ 位置外 , 在 $2\pi ,4\pi ,6\pi$ 等位置 , 都是 无限冲激响应 ,

其物理意义是 所有的能量 , 都集中在 $\omega =0$ 位置上 ;

周期信号 信息 都在其 周期组织区间内 , 其它区间都是周期性重复的 , 因此这里只分析 $[-\pi ,\pi ]$ 之间的信号 ;

$\tilde{\delta }(\omega )$ 的物理意义是 所有的能量 都集中在 $\omega =0,\pm 2\pi ,\pm 4\pi ,\cdots$ 位置上 ;

2、涉及公式介绍

傅里叶变换 : 时域 " 离散非周期 " 信号 , 其频域就是 " 连续周期 " 的 , 其频域 可以 展开成一个 " 正交函数的无穷级数加权和 " , 如下公式

$$X(e^{j\omega })=\sum _{n=-\infty }^{+\infty }x(n)e^{-j\omega n}$$

傅里叶反变换 : 利用 " 正交函数 " 可以推导出 " 傅里叶反变换 " , 即 根据 傅里叶变换 推导 序列 ;

$$x(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(e^{j\omega })e^{j\omega k}d\omega$$

3、1 的傅里叶反变换

将

$$X(e^{j\omega })=2\pi \tilde{\delta }(\omega )$$

带入到

$$x(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(e^{j\omega })e^{j\omega k}d\omega$$

傅里叶反变换 公式中 , 可以得到如下公式 :

$$ISFT[X(e^{j\omega })]=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }2\pi \tilde{\delta }(\omega )e^{j\omega k}d\omega$$

$-\pi$ ~ $\pi$ 之间 , 只有 $\omega =0$ 点有值为 $1$ , 其它点都为 $0$ ,

• 当 $\omega =0$ 时 , 结果是 $2\pi$
• 当 $\omega \ne 0$ 时 , $\tilde{\delta }(\omega )=0$ , 结果都是 $0$ ;

因此 ,

$${\int }_{-\pi }^{\pi }X(e^{j\omega })e^{j\omega 以上是关于数字信号处理序列傅里叶变换\; (\; 基本序列的傅里叶变换\; |\; 求\; 1\; 的傅里叶变换\; )的主要内容，如果未能解决你的问题，请参考以下文章}$$

数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | e^jωn 的傅里叶变换 )

数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | e^jωn 的傅里叶变换 )

数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | 单位脉冲序列 δ(n) 傅里叶变换 )

数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | 求 a^nu(n) 的傅里叶变换 )

数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | 求 a^nu(n) 的傅里叶变换 )

数字信号处理序列傅里叶变换 ( 基本序列的傅里叶变换 | 单位脉冲序列傅里叶变换 )