一元线性回归方程的计算步骤

Posted 2023-05-17

1、列计算表，求∑x，∑xx，∑y，∑yy，∑xy。

2、计算Lxx，Lyy，LxyLxx=∑(x-xˇ)(x-xˇ)Lyy=∑(y-yˇ)(y-yˇ)Lxy=∑(x-xˇ)(y-yˇ)

3、求相关系数，并检验；r = Lxy /( Lxx Lyy)1/2

4、求回归系数b和常数a；b=Lxy /Lxxa=y - bx

5、列回归方程。

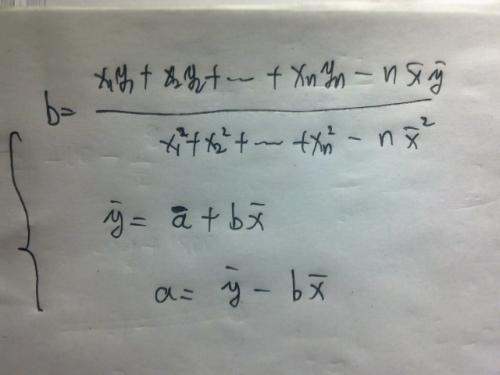
扩展资料：

根据最小平方法或其他方法，可以从样本数据确定常数项A与回归系数B的值。A、B确定后，有一个X的观测值，就可得到一个Y的估计值。回归方程是否可靠，估计的误差有多大，都还应经过显著性检验和误差计算。有无显著的相关关系以及样本的大小等等，是影响回归方程可靠性的因素。

如果只有一个自变量X，而且因变量Y和自变量X之间的数量变化关系呈近似线性关系，就可以建立一元线性回归方程，由自变量X的值来预测因变量Y的值，这就是一元线性回归预测。

如果因变量Y和自变量X之间呈线性相关，那就是说，对于自变量X的某一值 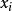 ，因变量Y对应的取值  不是唯一确定的，而是有很多的可能取值，它们分布在一条直线的上下，这是因为Y还受除自变量以外的其他因素的影响。

这些因素的影响大小和方向都是不确定的，通常用一个随机变量(记为  )来表示。

参考资料来源：百度百科——一元线性回归方程

参考技术A

1. 列计算表，求∑x，∑xx，∑y，∑yy，∑xy。
2.计算Lxx，Lyy，Lxy
Lxx=∑(x-xˇ)(x-xˇ)
Lyy=∑(y-yˇ)(y-yˇ)
Lxy=∑(x-xˇ)(y-yˇ)
3.求相关系数，并检验；
r = Lxy /( Lxx Lyy)1/2
2. 求回归系数b和常数a；
b=Lxy /Lxx
a=y - bx
3. 列回归方程。

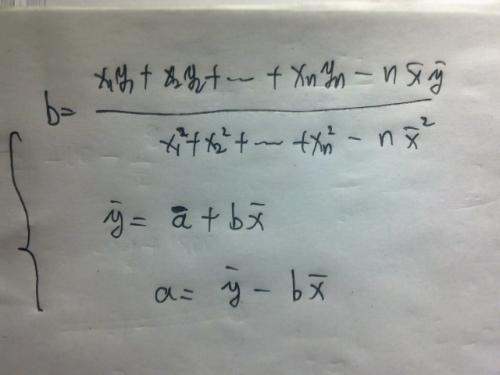
多元线性回归的模型可以是一元模型吗

第11章 一元线性回归
11.1 变量间关系的度量
变量之间的关系可分为两种类型，即函数关系和相关关系。其中，函数关系是一一确定的关系，给定一个自变量x，因变量y依确定的关系取相应的值；变量之间存在的不确定性的数量关系，则称为相关关系。

相关系数
相关关系可以通过散点图和相关系数来反映。相关系数是根据样本数据计算的度量两个变量之间线性关系强度的统计量，其计算公式为：

按照上述公式计算的相关系数也称为线性相关系数，或称为Pearson相关系数。
r的取值范围是[-1, 1]。若0 < r ≤ 1，表明x与y之间存在正线性相关关系；若-1 ≤ r < 0，表明x与y之间存在负线性相关关系。
r具有对称性，rxy = ryx。

11.2 一元线性回归
描述因变量y如何依赖自变量x和误差项ε的方程称为回归模型。只涉及一个自变量的一元线性回归模型可表示为：

回归模型中，假定ε的期望值等于0，因此y的期望值E(y) = β0 + β1x，也就是说，y的期望值是x的线性函数。描述因变量y的期望值如何依赖于自变量x的方程称为回归方程。
若总体回归参数 β0和 β1是未知的，必须利用样本去估计它们。用样本统计量去代替回归方程中的未知参数 β0和 β1，这时就得到了估计的回归方程。对于一元线性回归，估计的回归方程形式为：

最小二乘法就是通过使因变量的观测值yi与估计值之间的离差平方和最小来估计β0和 β1。

回归直线与各观测点的接近程度称为回归直线对数据的拟合优度。因变量y的取值是不同的，y取值的这种波动称为变差。n次观测值的总变差可由这些离差的平方和来表示，称为总平方和(SST)：

总平方和可以分解为两部分：回归值与均值的离差平方和称为回归平方和(SSR)；实际观测点与回归值的残差的平方和称为残差平方和或误差平方和(SSE)。回归平方和占总平方和的比例称为判定系数(R2)：

判定系数R2测度了回归直线对观测数据的拟合程度。R2的取值范围是[0, 1]，R2越接近1，回归的拟合度就越好。相关系数r实际上是判定系数的平方根。
判定系数可用于度量回归直线的拟合程度，而残差平方和则可以说明实际观测值与回归估计值之间的差异程度。估计标准误差就是度量各实际观测点在直线周围的散布状况的一个统计量，它是均方残差的平方根，用se来表示，其计算公式为：

估计标准误差是对误差项ε的标准差σ的估计，反映了用估计的回归方程预测因变量y时预测误差的大小。

11.3 利用回归方程进行预测
利用估计的回归方程，对于x的一个特定值x0，求出y的一个估计值的区间就是区间估计。区间估计包括置信区间估计和预测区间估计。

置信区间估计
置信区间估计是对x的一个给定值x0，求出y的平均值的区间估计。设x0为自变量x的一个特定值或给定值；E(y0)为给定x0时因变量y的平均值或期望值。一般来说，估计值不能精确地等于E(y0)。对于给定的x0，可以使用以下公式计算估计值标准差：

有了估计值的标准差之后，对于给定的x0，E(y0)在1-α置信水平下的置信区间可以表示为：

当x0=x均值时，估计值y的标准差的估计量最小，估计是最准确的。x0偏离均值越远，y的平均值的置信区间就变得越宽，估计效果越不好。

预测区间估计
预测区间估计是对x的一个给定值x0，求出y的一个个别值的区间估计。
为求出预测区间，首先必须知道用于估计的标准差，y的一个个别值y0的标准差的估计量sind计算公式如下：

对于给定的x0，y0在1-α置信水平下的预测区间可表示为：

和置信区间相比，预测区间的根号内多了一个1。因此，即使是对同一个x0，置信区间和预测区间的宽度也是不一样的，预测区间要比置信区间宽一些。两者的差别表明，估计y的平均值比预测y的一个特定值更精确。

第12章 多元线性回归
12.1 多元回归模型
在实际问题中，影响因变量的因素往往有多个，这种一个因变量同多个自变量的回归问题就是多元回归。
设因变量为y，k个自变量分别为x1，x2，…，xk，描述因变量y如何依赖自变量x1，x2，…，xk和误差项ε的方程称为多元回归模型：

与一元线性回归类似，多元线性回归模型的ε项有以下基本假定：误差项ε是一个期望为0的随机变量；对于自变量的所有值，ε的方差σ2都相同；误差项ε是一个服从正态分布的随机变量，且相互独立，ε~N(0, σ2)。

根据回归模型的假定，有：

上式称为多元回归方程，它描述了因变量y的期望值与自变量之间的关系。

回归方程中的参数β是未知的，需要利用样本数据去估计它们，当用样本统计量去估计回归方程中的位置参数时，就得到了估计的多元回归方程：

回归方程中样本统计量也可以根据最小二乘法求得，也就是使残差平方和最小，让残差平方和关于参数的偏导数为零可以求解。

12.2 显著性检验
线性关系检验是检验因变量y与k个自变量之间的关系是否显著，也称为总体显著性检验。检验的具体步骤如下：

提出假设。
H0：β1=β2=…=βk=0
H1：β1，β2，…，βk至少有一个不等于0
计算检验系数的统计量F。
回归平方和SSR和残差平方和SSE的计算方式同一元回归。

作出统计决策。
给定显著性水平α， 根据分子自由度=k， 分母自由度 = n - k - 1查F分布表得Fα。若F > Fα，则拒绝原假设，即自变量与因变量的线性关系是显著的。
在回归方程通过线性关系检验后，还要对各个回归系数βi有选择地进行一次或多次检验。回归系数检验的具体步骤如下：

提出假设。对于任意参数βi( i = 1, 2, …, k )有
H0：βi = 0
H1：βi ≠ 0
计算检验的统计量t

作出统计决策。给定显著性水平α， 根据自由度 = n - k - 1查t分布表，得tα/2的值。若 | t | > tα/2，则拒绝原假设，自变量对因变量的影响是显著的。
12.3 多重共线性与变量选择
当回归模型中使用两个或两个以上的自变量彼此相关时，则称回归模型中存在多重共线性。

当出现下列情况，暗示存在多重共线性：

模型中各对自变量之间显著相关；
当模型的线性关系显著时，几乎所有回归系数βi的t检验却不显著；
回归系数的正负号与预期的相反。
当回归模型存在多重共线性时，可以将相关的自变量进行剔除。

变量选择与逐步回归
在建立回归模型时，希望尽可能用最少的变量来建立模型。选择自变量的原则通常是对统计量进行显著性检验：讲一个或一个以上的自变量引入回归模型时， 是否使残差平方和(SSE)显著减少。如果增加一个自变量使SSE显著减少，则说明有必要将这个自变量引入回归模型，否则就没有必要将这个自变量引入。

文章知识点与官方知识档案匹配
算法技能树首页概览
31609 人正在系统学习中
打开CSDN，阅读体验更佳

Excel-一元线性回归和多元线性回归(借助数据分析功能和直接计算)_君琴...
一元线性回归 1、女士的身高-体重例子。–借助excel数据分析功能 使用excel中散点图功能将数据绘制成散点图。 散点图右键,选择“设置趋势线格式”。 弹出的设置框可以设置散点图样式,趋势线选择线性,勾选显示公式、显示R平方值。
继续访问
线性回归原理---简单线性回归、多元线性回归_温旧酒一壶~的博客-CSDN...
线性回归是回归分析的一种,评估的自变量X与因变量Y之间是一种线性关系,当只有一个自变量时,成为简单线性回归,当具有多个变量时,称为多元线性回归。 线性关系的理解: >画出来的图像是直的(简单线性回归是直线,多元线性回归是超平面) ...
继续访问
一元线性回归与多元线性回归
线性回归action精讲 线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。 一元与多元 回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关...
继续访问
一元线性回归VS多元线性回归
      一元线性回归和多元线性回归表面意思容易理解，但是结合实际的数据集，会混乱。这也是在编写线性回归博文的时候梳理知识点发现自己的不足，同时记录下来，让有疑问的同学也可以得到答案，拨开乌云。 1.在数据集上的异同 一元线性回归： 给定数据集，其中，样本有1个属性描述。 VS 多元线性回归： 给定数据集，其中 ，，样本有d个属性描述。   2.向量表达式 一元线性回归：  ...
继续访问
最新发布 机器学习：回归分析—— 一元线性回归、多元线性回归的简单实现
机器学习：回归分析—— 一元线性回归、多元线性回归的简单实现
继续访问

机器学习——一元线性回归和多元线性回归
一元线性回归：梯度下降法 一元线性回归是线性回归的最简单的一种，即只有一个特征变量。首先是梯度下降法，这是比较经典的求法。一元线性回归通俗易懂地说，就是一元一次方程。只不过这里的斜率和截距要通过最小二乘和梯度下降法不断迭代找到最优解。我们先来看看运用到的代价函数：最小二乘法。 这其实和高中学的最小二乘法一模一样，不过值得注意的是，这里的2其实是可以消去的，这对结果的影响不大，之所以保留是因为，方便与之后求导所得的2消掉。 梯度下降法： 开始就说过，斜率和截距是要通过迭代计算求得的。因为初始化的斜率和截距所
继续访问

R语言 一元线性回归、多元线性、多项式回归
关注微信号：小程在线 关注CSDN博客：程志伟的博客 R版本：3.6.1 本节主要介绍了一元线性回归、多元线性、多项式回归。 重点介绍了summary里面每个参数的意义； 创建训练集、测试集； 多项式poly()函数以及I()函数的使用。 ###########一元线性回归############# > library(MASS) > data(Boston) #...
继续访问

线性回归（一）---一元线性回归
线性回归（一） 线性回归是分析因变量与自变量呈现线性关系的一种方法，来确定一个因变量如何依赖一个或多个自变量的变化而变化，运用十分广泛。 在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，，则称为多元线性回归分析。 线性回归常用参数： regression.intercept_ ： 截距， 默认为True，可选False regression.coef_ ：
继续访问

机器学习--一元线性回归
线性方程    线性方程可以分为：一元线性方程，多元线性方程，广义线性方程。    一元线性方程是指拥有一个自变量一个因变量的方程，如y=ax+b    多元线性方程是指拥有多个自变量一个因变量的方程，如y=ax+bz+c    广义线性方程是指非线性方程问题可以使用线性求解。 ...
继续访问

什么是预测区间和置信区间
什么是预测区间和置信区间 最近需要画带有置信区间的拟合图，其中在matlab的doc中搜索“Confidence and Prediction Bounds”，出现了两种置信区间。 原博客：https://www.cnblogs.com/100thMountain/p/5539024.html 置信区间估计 (confidence interval estimate)：利用估计的回归方程，对于自变...
继续访问
一元线性回归个人梳理
一元线性回归 回归定义： 回归分析(regression analysis)用来建立方程模拟两个或者多个变量之间如何关联 被预测的变量叫做：因变量(dep 参考技术A 日只涉及一个自变量的一元线性回归模型可表示为: 回归模型中,