一元线性回归的数学原理

Posted 2023-05-17

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了一元线性回归的数学原理相关的知识，希望对你有一定的参考价值。

一元线性回归其实就是最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。

利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

根据最小平方法或其他方法，可以从样本数据确定常数项A与回归系数B的值。A、B确定后，有一个X的观测值，就可得到一个Y的估计值。

回归方程是否可靠，估计的误差有多大，都还应经过显著性检验和误差计算。有无显著的相关关系以及样本的大小等等，是影响回归方程可靠性的因素。

扩展资料：

在给定了X和Y的样本观察值之后，离差平方总和的大小依赖于a和b的取值，客观上总有一对a和b的数值能够使离差平方总和达到最小。利用微分法求函数极值的原理。

在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。最常用的线性回归建模是给定X值的y的条件均值是X的仿射函数。

不太一般的情况，线性回归模型可以是一个中位数或一些其他的给定X的条件下y的条件分布的分位数作为X的线性函数表示。像所有形式的回归分析一样，线性回归也把焦点放在给定X值的y的条件概率分布，而不是X和y的联合概率分布（多元分析领域）。

参考资料来源：百度百科——一元线性回归方程

参考技术A 一元线性回归的数学原理为：一元线性回归也可以叫做最小二乘法，这种乘法也叫做最小平方法，它是一种数学优化的技术。一般会经由最小化误差的平方与寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
估计方法很多，最小二乘只是其中一种。具体原理如果没有学过偏导数就不必深究了。
另外，一元线性回归的回归分析通常会牵扯到两个变量的，被称为一元回归分析。医院回归的主要任务是把两个相关变量中的一个变量去估计另一个变量，被估计的变量，称因变量，可设为Y；估计出的变量，称自变量，设为X。回归分析就是要找出一个数学模型Y=f(X)，使得从X估计Y可以用一个函数式去计算。当Y=f(X)的形式是一个直线方程时，称为一元线性回归。
这个方程一般可表示为Y=A+BX。根据最小平方法或其他方法，可以从样本数据确定常数项A与回归系数B的值。A、B确定后，有一个X的观测值，就可得到一个Y的估计值。回归方程是否可靠，估计的误差有多大，都还应经过显著性检验和误差计算。有无显著的相关关系以及样本的大小等等，是影响回归方程可靠性的因素。参考技术B 一元线性回归其实就是最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。估计方法很多，最小二乘只是其中一种。具体原理如果没有学过偏导数就不必深究了。

数学建模天天学_第四天_多元线性回归模型

附上川川大佬博客的pdf

自我理解：

一、一元线性回归

一元回归方程比较简单，我们只需要自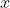变量,因变量的部分数据，经过绘出散点图，就可以进行拟合。

1.例题数据

2.转换代码

x=[168 145 128 138 145 135 127 111 102 94];
y=[661 631 610 588 583 575 567 502 446 379];

3.Matalb绘图

clc;
clear;
x=[168 145 128 138 145 135 127 111 102 94];
y=[661 631 610 588 583 575 567 502 446 379];
for i=1:10
    plot(x(i),y(i),'or');
    %plot(X,Y) 创建 Y 中数据对 X 中对应值的二维线图。
    %o代表以圆圈为图像，r为'red'红色。
    hold on
    %添加新绘图时保留当前绘图，使所有点一起绘出。
end
xlabel('x');%x轴元素为x
ylabel('y');%同上

效果图

此时我们已经可以进行拟合，因为它的点大致处于一条直线附近，但是我们可以发现，x与y似乎是对数关系，所以可以进行进一步的精细。

4.进一步拟合分析

由此经过观察我们可以另作,对z与x进行绘图。

clc;
clear;
x=[168 145 128 138 145 135 127 111 102 94];
y=[661 631 610 588 583 575 567 502 446 379];
z=zeros(size(x));
%获得向量x的大小
n=length(x);
%获得向量x的长度
for i=1:n
    z(i)=log(x(i));
    plot(x(i),z(i),'or');
    %plot(X,Y) 创建 Y 中数据对 X 中对应值的二维线图。
    %o代表以圆圈为图像，r为'red'红色。
    hold on
    %添加新绘图时保留当前绘图，使所有点一起绘出。
end
xlabel('x');%x轴元素为x
ylabel('z');%同上

效果图

现在可以看出它的拟合效果更加直观。

5.获得回归方程

根据第④步得到的图像，我们可以近似看为一条的直线。

因此

clc;
clear;
x=[168 145 128 138 145 135 127 111 102 94];
y=[661 631 610 588 583 575 567 502 446 379];
z=zeros(size(x));
%获得向量x的大小
n=length(x);
%获得向量x的长度
for i=1:n
    z(i)=log(x(i));
end
%p = polyfit(x,y,n)返回次数为 n 的多项式 p(x) 的系数
p=polyfit(x,z,1)

结果有：

二、多元线性回归

1、模型

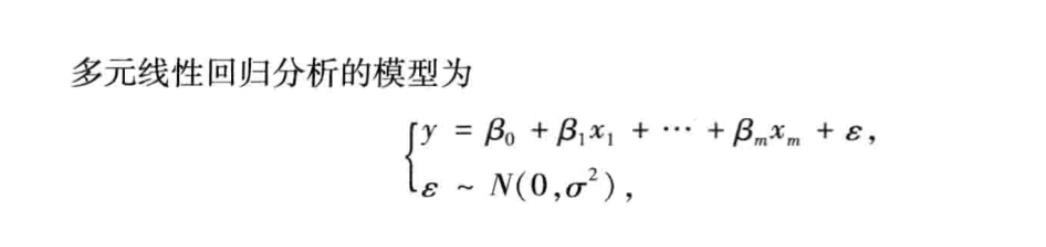
基础为最小二乘法

在Matlab中可以用到函数

[b,bint,r,rint,stats]=regress(y,x，alpha)

2、例题

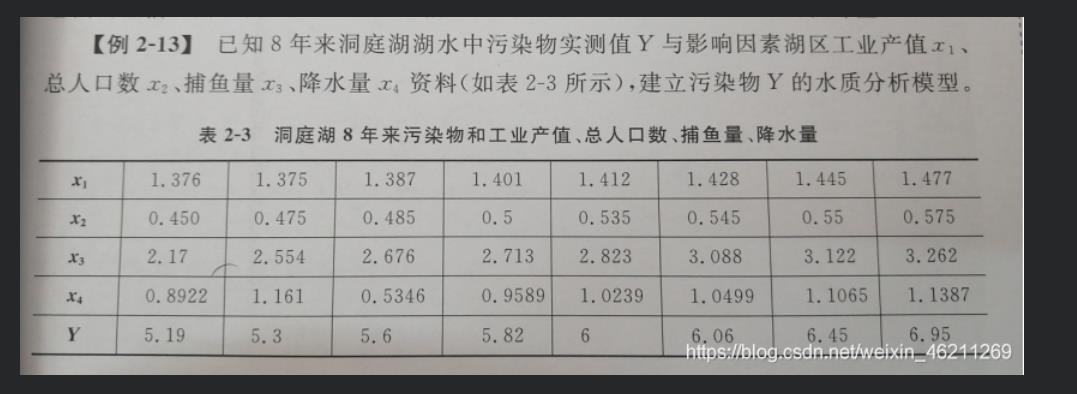
3、Matlab实现

clc;
clear;
x1=[1.376 1.375 1.387 1.401 1.412 1.428 1.445 1.477];
x2=[0.450 0.475 0.485 0.5 0.535 0.545 0.55 0.575];
x3=[2.17 2.554 2.676 2.713 2.823 3.088 3.122 3.262];
x4=[0.8922 1.161 0.5346 0.9589 1.0239 1.0499 1.1065 1.1387];
y=[5.19 5.3 5.6 5.82 6 6.06 6.45 6.95];
%数据输入
y=y';
%变为列向量
x=[ones(size(x1')),x1',x2',x3',x4'];
%构造成矩阵
[b,bint,r,rint,stats]=regress(y,x)

4、结果

因此由b的返回值可得

三、参考文档

%[b,bint,r,rint,stats]=regress(y,x)
https://ww2.mathworks.cn/help/stats/regress.html?s_tid=doc_ta
%plot
https://ww2.mathworks.cn/help/matlab/ref/plot.html?s_tid=srchtitle_plot_1
%ployfit
https://ww2.mathworks.cn/help/matlab/ref/polyfit.html?searchHighlight=ployfit&s_tid=srchtitle_ployfit_1
%hold on
https://ww2.mathworks.cn/help/matlab/ref/hold.html?searchHighlight=hold%20on&s_tid=srchtitle_hold%20on_1

以上是关于一元线性回归的数学原理的主要内容，如果未能解决你的问题，请参考以下文章