机器学习--线性回归的原理与基础实现

Posted 2021-12-07 胜天半月子

文章目录

• 一、一元线性回归的实现
• • 1.1 原理
  • 1.2 Python底层实现一元线性回归
• 二、多元线性回归的实现
• • 2.1 参考文献
  • 2.2 代码实现
  • 2.3 相关性分析
• 三、第三方库实现线性回归
• 四、线性回归案例
• • 4.1 回归知识复习
  • 4.2 案例编写

---

---

一、一元线性回归的实现

1.1 原理

• y=mx+c

y为结果，x为特征，m为系数，c为误差 在数学中m为梯度c为截距

最小二乘法求回归直线方程的推导过程

1.2 Python底层实现一元线性回归

• 导入包

import numpy as np
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
%matplotlib inline

• 计算

# 构造训练的数据集
x_train = [4,8,5,10,12]
y_train = [20,50,30,70,60]

# 定义函数求出斜率w和截距b
# 方法：使用最小二乘法斜率和截距求导并使得导数值等于0求解出斜率和截距
def fit(x_train,y_train):
    size = len(x_train)
    numerator = 0 # 初始化分子
    denominator = 0 # 初始化分母
    
    for i in range(size):
        numerator += (x_train[i]-np.mean(x_train)) * (y_train[i]-np.mean(y_train))
        denominator += (x_train[i]-np.mean(x_train)) ** 2
    
    w = numerator / denominator
    b = np.mean(y_train) - w * np.mean(x_train) # 用求出的斜率计算截距
    
    return w,b

# 预测函数
def predict(x,w,b):
    y = w * x + b
    return y

# 根据计算出的w,b进行画图
def fit_line(w,b):
    typ1 = plt.scatter(x_train,y_train,color='b') # 画出散点图
    # 测试集使用np.linspace()生成的数据集进行测试
    x = np.linspace(4,15,9)
    y = w * x + b
        
    typ2 = plt.scatter(x,y,color='red') # 测试集的散点图
    plt.plot(x,y)
    plt.legend((typ1,typ2),('train','test'))
    plt.show()

• 显示结果

w ,b = fit(x_train,y_train) # 根据训练集数据计算出斜率和截距
print('斜率：',w,'截距：',b)
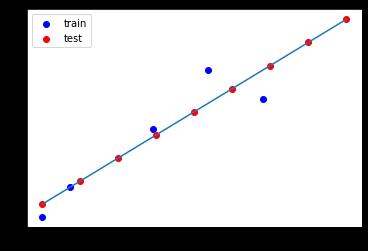
fit_line(w,b) # 绘制出测试集数据

斜率： 5.714285714285714 截距： 1.4285714285714306
x_test: [ 4. 5.375 6.75 8.125 9.5 10.875 12.25 13.625 15. ]
y_test: [24.28571429 32.14285714 40. 47.85714286 55.71428571 63.57142857
71.42857143 79.28571429 87.14285714]

---

二、多元线性回归的实现

2.1 参考文献

• 作者自己推导的：使用最小二乘法计算多元线性回归的公式推导⭐
• 系统介绍：机器学习中的线性代数之矩阵求导
• 作者自己的理解：最小二乘法（多元线性回归模型）
• 多变量相关性分析(一个因变量与多自变量)
• Scikit-learn中，性能评估所用的score到底是个什么意思（附Python实例）？

2.2 代码实现

# 导入模块
import numpy as np
import pandas as pd

# 构造数据，前三列表示自变量X，最后一列表示因变量Y
data = np.array([[3, 2, 9, 20],
                 [4, 10, 2, 72],
                 [3, 4, 9, 21],
                 [12, 3, 4, 20]])
print("data:", data, "\\n")

X = data[:, :-1] # 取 前三列
Y = data[:, -1]

# np.c_按列叠加两个矩阵，np.mat()数组转化为矩阵
# 将array数组转换为矩阵
X = np.mat(np.c_[np.ones(X.shape[0]), X])  # 为系数矩阵增加常数项系数
Y = np.mat(Y)  

# 根据最小二乘法对目标函数求导为0得到最优参数向量B 的解析公式如下：
B = np.linalg.inv(X.T * X) * (X.T) * (Y.T)
print("B:", B, "\\n")  # 输出系数,第一项为常数项，其他为回归系数

# 预测结果
print("1,60,60,60预测结果：", np.mat([1, 60, 60, 60]) * B, "\\n")  

# 多元线性相关分析
# 两个变量间的关系称为简单相关，多个变量称为偏相关或复相关
# 度量复相关程度的指标:复相关系数
# Y.size返回矩阵Y中元素的个数
Q_e = 0
Q_E = 0
Y_mean = np.mean(Y)
for i in range(Y.size):
    Q_e += pow(np.array((Y.T)[i] - X[i] * B), 2)
    Q_E += pow(np.array(X[i] * B) - Y_mean, 2)
R2 = Q_E / (Q_e + Q_E)
print("R2", R2)

最后结果中的Q_e与Q_E的数值：
Q_e: [[8.67070469e-24]]
Q_E: [[2002.75]]
(Q_e + Q_E): [[2002.75]]

• 涉及的numpy操作演示
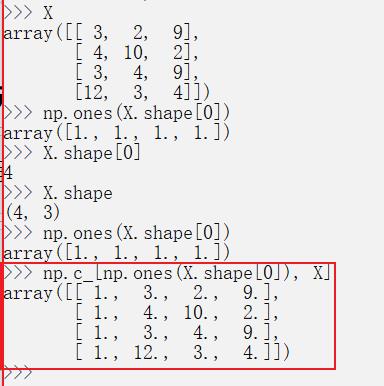
• np.c_

np.c_中的c 是 column(列)的缩写，就是按列叠加两个矩阵，就是把两个矩阵左右组合，要求行数相等。

• np.mat() 与np.array()

• np.mat()函数用于将输入解释为矩阵。
• np.array()函数用于创建一个数组。

• np.linalg.inv()与np.linalg.det()

• np.linalg.inv()：矩阵求逆
• np.linalg.det()：矩阵求行列式（标量）

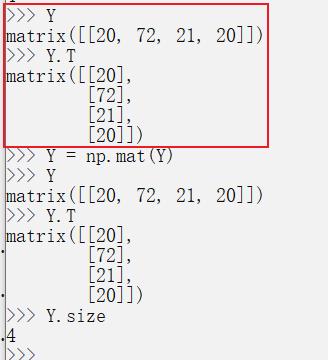
• .T与.size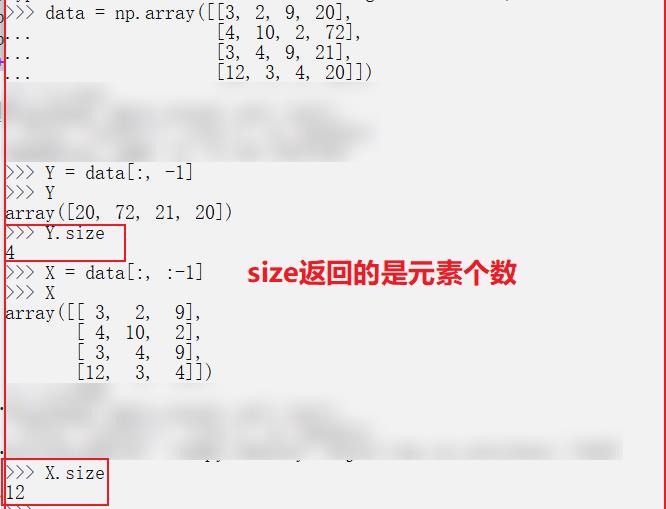
  

2.3 相关性分析

复相关分析:多元线性相关分析两个变量间的关系称为简单相关，多个变量称为偏相关或复相关，复相关指一个因素与多个因素之间的相关关系。

---

三、第三方库实现线性回归

# 导入sklearn下的LinearRegression 方法
from sklearn.linear_model import LinearRegression
import numpy as np

model = LinearRegression()

# 构造用于训练的数据集
x_train = np.array([[2, 4], [5, 8], [5, 9], [7, 10], [9, 12]])
y_train = np.array([20, 50, 30, 70, 60])

# 训练模型并输出模型系数和训练结果
model.fit(x_train, y_train)

# coef_ 系数w   intercept_截距b
print(model.coef_)  # 输出系数w
print(model.intercept_)  # 输出截距b
print(model.score(x_train, y_train))  # 输出模型的评估分数R2

[13.39207048 -6.03524229]
22.907488986784166
0.7433664583546766

四、线性回归案例

• 案例来源： 【菊安酱的机器学习】第7期 线性回归

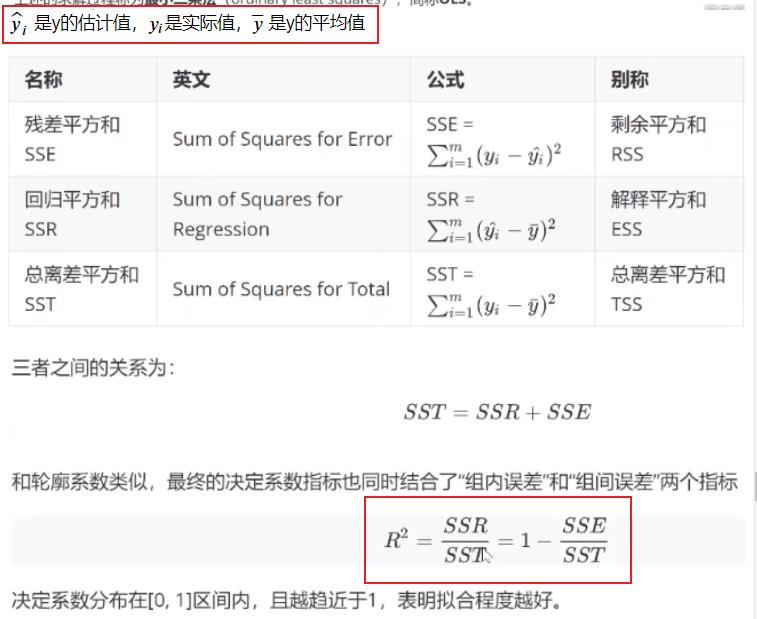
4.1 回归知识复习

• 简单线性回归
  
• 多元线性回归
  
• 线性回归的损失函数
  
  

4.2 案例编写

1. 导入包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['simhei']
%matplotlib inline

2. 导入数据集并探索数据

ex0 = pd.read_table('./data/ex0.txt',header=None)
ex0.head()

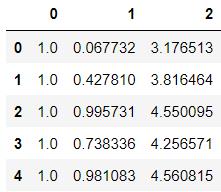
ex0.shape

(200, 3)

3. 构建辅助函数

# 方法：array数组转换为矩阵Maritx
def get_Mat(data):
    xMat = np.mat(data.iloc[:,:-1].values)
    yMat = np.mat(data.iloc[:,-1].values).T  # 200行1列
    return xMat,yMat


# 方法：可视化数据
def plotShow(data):
    xMat,yMat = get_Mat(data)
    plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5)# xMat.A[:,1]选择第一列的数据
    plt.show()

• 对其中不理解的程序进行展示

xMat,yMat = get_Mat(ex0)

yMat = np.mat(ex0.iloc[:,-1].values)
yMat # 1行200列
yMat.T  # 200行1列

xMat[:10]

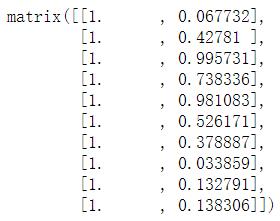
yMat[:10]

xMat.A[:10] # .A ： 矩阵转换成array的形式

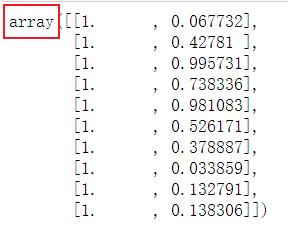
yMat.A[:10]

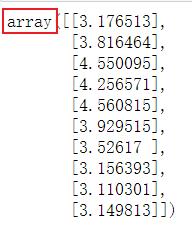
xMat.A[:,1][:10]

plotShow(ex0)

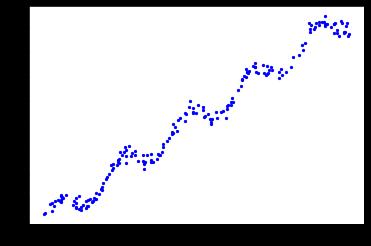
4. 计算回归系数

N阶方阵A为可逆的，重要条件是它的行列式不等于0，一般只要看它的行列式就可以啦。
矩阵可逆=矩阵非奇异=矩阵对应的行列式不为0=满秩=行列向量线性无关
det(A)指的是矩阵A的行列式（determinant），如果det(A)=0，则说明矩阵A是奇异矩阵，不可逆。
矩阵对象可以通过 .I更方便的求逆

"""
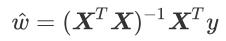
函数功能：计算回归系数
参数说明：
dataSet：原始数据集
返回：
ws：回归系数
"""
def standRegres(data):
    xMat,yMat = get_Mat(data)
    xTx = xMat.T * xMat
    if np.linalg.det(xTx) == 0:
        print('xMat矩阵为奇异矩阵，无法求逆！')
        return
    ws = xTx.I * (xMat.T*yMat)  #  .I:求逆
    return ws

xMat.shape

(200, 2)

xMat.T.shape

(2, 200)

ws = standRegres(ex0)
ws   # 分别对应x中第一列和第二列的系数 

matrix([[3.00774324],
[1.69532264]])

5. 绘制最佳拟合直线

"""
函数功能：绘制散点图和最佳拟合直线
"""
def plotReg(dataSet):
    plt.figure(figsize=(8,8))
    xMat,yMat=get_Mat(dataSet)
    plt.scatter(xMat.A[:,1],yMat.A,c='b',s=8)
    ws = standRegres(dataSet)
    yHat = xMat*ws # 使用矩阵进行计算  求出模型估计值
    print('yHat:',yHat[:15])
    plt.scatter(xMat.A[:,1],yHat.A,c='k',s=8)
    plt.plot(xMat[:,1],yHat,c='r')
    plt.show()

yMat[:15]

print('yHat:',yHat[:15])# 求出的模型估计值

plotReg(ex0)

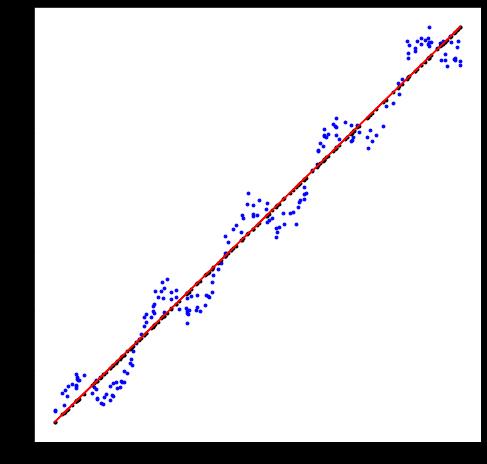
6. 求出相关系数

在python中，Numpy库提供了相关系数的计算方法：可以通过函数np.corrcoef(yEstimate,yActual)来计算预测值和真实值之间的相关性。这里需要保证的是，输入的两个参数都是行向量。

xMat,yMat =get_Mat(ex0)# 转换为矩阵
ws=standRegres(ex0) # 预测
yHat = xMat*ws # 估计值
np.corrcoef(yHat.T,yMat.T) #保证两个都是行向量

• Python Numpy库 numpy.corrcoef()函数讲解
• np.corrcoef(yHat.T,yMat.T)的矩阵的行数=列数=矩阵1的行数+矩阵2的行数

yHat.shape

(200, 1)

yMat.T.shape

(1, 200)

后续学了相关优化方法会进行总结，请大家耐心等待！