多元线性回归公式的计算方法？

Posted 2023-05-09

参考技术A

多元线性回归：

1.打开数据，依次点击：analyse--regression，打开多元线性回归对话框。

2.将因变量和自变量放入格子的列表里，上面的是因变量，下面的是自变量。

3.设置回归方法，这里选择最简单的方法：enter，它指的是将所有的变量一次纳入到方程。其他方法都是逐步进入的方法。

4.等级资料，连续资料不需要设置虚拟变量。多分类变量需要设置虚拟变量。

5.选项里面至少选择95%CI，点击ok。

计算模型

一元线性回归是一个主要影响因素作为自变量来解释因变量的变化，在现实问题研究中，因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归亦称多重回归。

当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元线性回归。 　

设y为因变量X1,X2…Xk为自变量，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：

Y=b0+b1x1+…+bkxk+e

机器学习之线性回归

文章目录

• 评价方法
• 一元线性回归
• • np.polyfit求解
  • 带入公式求解
  • 化简公式求解
  • lstsq求解
• 多元线性回归
• • 代码实现
• 一元多项式回归
• • 代码实现
• 参考

评价方法

回归问题有很多的评价方法。

这里主要想写一下R^2的计算方法。
需要计算R^2需要先弄清楚以下几个误差的计算方法：

SSE

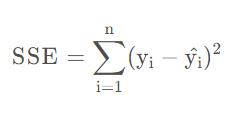
SSE为误差平方和，是指预测值和原样本值之间的误差。

SSR

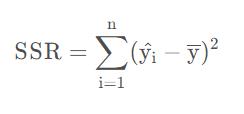
SSR为回归平方和，是指预测值和真实值之间的波动情况。

SST

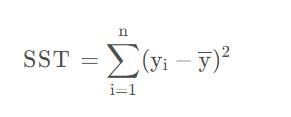
SST是指总偏差平方和，是指真实值的波动情况。

不难发现SSR + SSE = SST

R^2的定义为SSR / SST = 1 - SSE/SST

R^2的评价标准如下：

一元线性回归

首先给出一点点数据用作示例。

# coding:utf-8
# 2022.9.5
import matplotlib.pyplot as plt
x = [6, 8, 10, 14, 18]
y = [7, 9, 13, 17.5, 18]
plt.scatter(x, y)
plt.xlabel("D")
plt.ylabel("price")
plt.grid()
plt.show()

画个图看看：

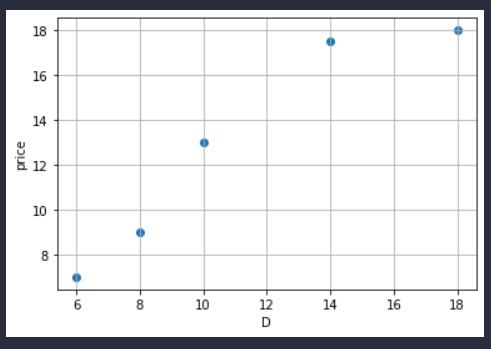
这是一个披萨直径和价格（x, y）的数据
看图我们可以发现，拟合出的直线k一定是大于0的。
接下来我们看一下西瓜书里关于线性回归的介绍：

以我们一元的数据为例，那么就是一元线性回归，比较简单。
那么就是求：

这里我们可以考虑成有那么一个wxi + bi的解析式，带入我们数据的x得出的y与真实的y越接近那么这个模型肯定拟合的越好的。

那么用什么来衡量这个接近呢？

课上老师提了三种：

1. xi - xj => 0
2. |xi - xj| => 0
3. (xi - xj)^2 => 0
   第一种是xi和xj的差越趋近于0越接近
   第二种是xi和xj的差的绝对值越接近于0越接近
   第三种是xi和xj的差的平方和越接近于0越接近

明显第三种好，但是为什么呢？

原因如下：

1. 会相互抵消
2. 不是处处可导
3. 处处可导
   因此选择第三种来衡量接近。
   那么问题就解决一半了，因为只需要求解出来就行了。
   
   西瓜书上也是这么个意思。
   现在就是要求3.4式子值最小的w和b就可以解决一元线性回归的问题了。
   
   
   
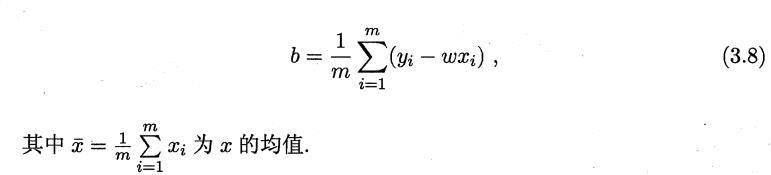
   公式可能一下子看不懂怎么来的，没事，自己推以下就可以了。
   自己不会推的话可以参考一下这篇：
   机器学习之线性回归(手推公式版)
   看人家推一遍也可以。
   
   这里是补充内容，为了严谨。
   到了这里，一元线性回归的逻辑解已经写出来了，那么如何带到上面那个示例真真切切算出来呢？
   最开始想到最快的方法是numpy:

np.polyfit求解

import numpy as np
# x: 类数组，形状（M，），表示M个采样点的x坐标
# y: 类似array_，形状为（M，）或（M，K）, 表示采样点的y坐标。
# 通过传递每列包含一个数据集的2D数组，可以一次拟合多个共享相同x坐标的采样点数据集
# deg: 度：整数, 表示拟合多项式的度
poly = np.polyfit(x,y,deg=1)
print(poly)
z = np.polyval(poly, x)
plt.scatter(x, y, label="True")
plt.plot(x, z, label="Pre", color="red")
plt.xlabel("D")
plt.ylabel("price")
plt.grid()
plt.legend()
plt.show()

运行结果：

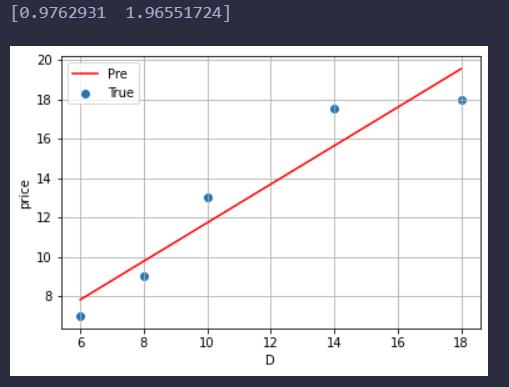
poly输出前面那个是w后面那个是b
得出的结果确实是k>0

带入公式求解

其实我们也可直接套西瓜书的一元求解公式：

import numpy as np
x = [6, 8, 10, 14, 18]
y = [7, 9, 13, 17.5, 18]

def get_w(x, y):
    x_mean = np.mean(x)
    m = len(x)
    res1 = 0 # 公式上面部分
    res2 = 0  # 公式下面左边部分
    for i in range(m):
        res1 += y[i] * (x[i] - x_mean) 
        res2 += np.power(x[i], 2)
    return res1 / (res2 - np.power(np.sum(x), 2) / m)
w = get_w(x, y)
print(w)

def get_b(x, y, w):
    b = 0
    m = len(x)
    for i in range(m):
        b += y[i] - w * x[i]
    return b / m
b = get_b(x, y, w)
print(b)

运行结果：

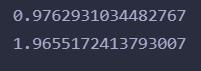
没什么毛病。

化简公式求解

然后老师上课说到，求出的解其实可以看成：
w = cov(x, y) / var(x)
b = $\overline{y}$ - w$\overline{x}$
算了一下：

import numpy as np
var = np.var(x, ddof=1) # 贝塞尔矫正
x = np.array(x)
y = np.array(y)
y_bar = y.mean()
x_bar = x.mean()
cov = np.multiply((x - x_bar).transpose(), (y - y_bar)).sum() / (x.shape[0] - 1)
var_x = np.var(x, ddof=1)
w = cov / var_x
b = y_bar - w * x_bar
print(w)
print(b)

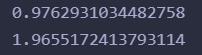
确实没毛病。

lstsq求解

也可以用numpy里的lstsq来求：

from numpy.linalg import lstsq
x = [[6, 8, 10, 14, 18], [1, 1, 1, 1, 1]]
x = np.array(x)
print(y.reshape(-1, 1).shape)
print(lstsq(x.transpose(), y.reshape(-1, 1)))
# lstsq的输出包括四部分：回归系数、残差平方和、自变量X的秩、X的奇异值。一般只需要回归系数就可以了。

当然还有很多很多求解方式。

求解完了我们可以评价一下模型：
理论上应该用测试集来评价（模型没见过的数据）
但是这里就用训练集浅浅套用一下：

x = [6, 8, 10, 14, 18]
y = [7, 9, 13, 17.5, 18]
x = np.array(x)
y = np.array(y)
pre_y = x * w + b
print(pre_y)
print(y)
print(np.power(pre_y - y, 2))
SSR = np.power(pre_y - y.mean(), 2).sum()
SST = np.power(y - y.mean(), 2).sum()
SSE = np.power(y - pre_y, 2).sum()
# R^2 = 1 - SSres / SStot
print(SSR, SST, SSE)
print(SSR + SSE)
print(1 - SSE / SST)

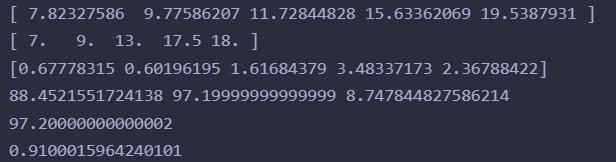
确实验证了SSR + SSE = SST（计算机小数会飘，实际上是相等的）
计算出的训练集的R^2 = 0.91
看上去蛮不错，但是应该再看测试集才能综合评价模型，因为这里没留测试集，就这样吧。

多元线性回归

一元的情况确实特殊，用各种方法都能乱解，但是多元的情况才是更加符合实际的，因此计算起来还是需要通过矩阵运算会比较有效率，之前遍历套公式就显得效率低下不太行了。

不过计算的思路还是一样的，只不过换成矩阵运算了。

为什么这里d+1维？
因为原本特征d个加上偏置b（被吸入w向量了）就相当于看成d+1维的向量了。
同样的思路求出w向量即可


后面还没看就不继续了。
多元公式推导也可以看
机器学习之线性回归(手推公式版)

代码实现

x = [[6,8,10,14,18],[2,1,0,2,0],[1,1,1,1,1]]
y = [[7],[9],[13],[17.5],[18]]
# y = w1 * x1 + w2 * x2 + b
from turtle import mode
from numpy.linalg import inv
from numpy import dot, transpose
x = np.array(x)
y = np.array(y)
x = x.transpose()
print(dot(inv(dot(transpose(x), x)), dot(transpose(x), y)))


from numpy.linalg import lstsq
print(lstsq(x, y))

两种代码解出结果是一样的

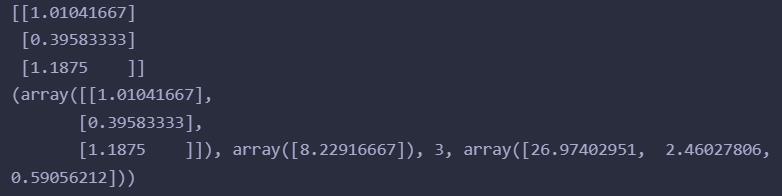
一元多项式回归

假设需要拟合一个最高次只有2的一元多项式。
那么此时思路也是和之前一样，算法也是。
就是求一个y = a0 + a1 * x + a2 * x ^2中的a0、a1、a2
带入x之后其实就是相当于求多元线性回归。
以开始的例子为例，求直径的多项式（最高次为2）的拟合曲线：

代码实现

x = [[6,8,10,14,18],[6 ** 2,8 ** 2,10 ** 2,14 ** 2,18 ** 2],[1,1,1,1,1]]
y = [[7],[9],[13],[17.5],[18]]
# y = w1 * x1 + w2 * x2 + b
from turtle import mode
from numpy.linalg import inv
from numpy import dot, transpose
x = np.array(x)
y = np.array(y)
x = x.transpose()
print(dot(inv(dot(transpose(x), x)), dot(transpose(x), y)))


from numpy.linalg import lstsq
print(lstsq(x, y))

两种方式解出结果是一样的

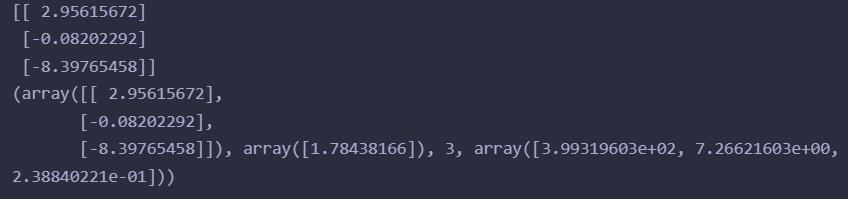
参考

#深度解析# SSR，MSE，RMSE，MAE、SSR、SST、R-squared、Adjusted R-squared误差的区别
机器学习07：线性回归评估 SST、SSE、SSR、R2
衡量线性回归法的指标：MSE, RMSE和MAE
周志华-机器学习