多元线性回归方程公式

Posted 2023-05-09

参考技术A 问题一：多元线性回归的方程公式 Y= a + b1X1 + b2X2 + … + bkXk

问题二：高分悬赏求数学达人帮忙，基于如图所示的EXCEL表格数据写出多元线性回归方程的偏回归系数的计算公式 1、在“数据”选项下的“数据分析”中，选择“回归”；
2、在“回归”中，选择Y值输入区域为A2:A7，X值输入区域为B2:D7，勾选默认的置信度95%，输出选项中的输出区域选择当前表格的F1单元格，确定；
3、F3:G8是“回归统计表”,F10:K14为“方差分析表”，F16:N20为回归参数表；
4、由回归统计表可以看出，数据之间的相关程度不大，相关性不明显，根据回归参数表，得到多元线性回归方程为y=-43.8823+0.49046*x_1+0.358891*x_2+0.495528*x_3

问题三：多元线性回归模型公式在word里怎么输入 公式编辑器当然可输入多元回归方程组

问题四：多元线性回归分析模型中估计系数的方法是什么 多元线性回归分析模型中估计系数的方法是：多元线性回归分析预测法

多元线性回归分析预测法：是指通过对两个或两个以上的自变量与一个因变量的相关分析，建立预测模型进行预测的方法。当自变量与因变量之间存在线性关系时，称为多元线性回归分析。

多元线性回归预测模型一般公式为： 多元线性回归模型中最简单的是只有两个自变量（n=2）的二元线性回归模型，其一般形式为：
下面以二元线性回归分析预测法为例，说明多元线性回归分析预测法的应用。
二元线性回归分析预测法，是根据两个自变量与一个因变量相关关系进行预测的方法。二元线性回归方程的公式为：式中：：因变量；
x1,x2：两个不同自变量，即与因变量有紧密联系的影响因素。
a,b1,b2：是线性回归方程的参数。
a,b1,b2是通过解下列的方程组来得到。
二元线性回归预测法基本原理和步骤同一元线性回归预测法没有原则的区别，大体相同。
“多元线性回归分析预测法”百度百科链接：baike.baidu/view/1338395

问题五：如何用Excel求多元线性回归方程 5分 excel貌似不能求多元回归方程，只能使用数据分析工具进行回归分析，不过求一元回归方程是可以的。
如果要求多元回搐方程，需要用到专业统计软件，如spss等。

线性回归的基本概念以及正规方程

目录

• 前言
• 1.基本概念
• • 1.1 连续值
  • 1.2 离散值
  • 1.3 简单线性回归
  • 1.4 基本名词的定义
  • 1.5 多元线性回归
• 2.正规方程
• • 2.1 最小二乘法的矩阵表示
  • 2.2 多元一次方程举例
  • • 2.2.1 二元一次方程
    • 2.2.2 三元一次方程
    • 2.2.3 八元一次方程
    • 2.2.4 $sklearn$ 算法使用
    • 2.2.5 带截距的线性方程
    • • 2.2.5.1 增加截距 $12$
      • 2.2.5.2 修改数据 $X$
  • 2.3 矩阵转置公式与求导公式
  • 2.4 推导正规方程 $\theta$ 的解
  • 2.5 凸函数判定

前言

本文属于 线性回归算法【AIoT阶段三】（尚未更新），这里截取自其中一段内容，方便读者理解和根据需求快速阅读。

线性回归是机器学习中有监督机器学习下的一种算法。 回归问题主要关注的是因变量(需要预测的值，可以是一个也可以是多个)和一个或多个数值型的自变量(预测变量)之间的关系。

需要预测的值:即目标变量，target，y，连续值预测变量。

影响目标变量的因素：$X_1$…$X_n$，可以是连续值也可以是离散值。

因变量和自变量之间的关系:即模型，model，是我们要求解的。

1.基本概念

1.1 连续值

🚩连续值就是连续的一连串数字，是可以无限细分下去的一段，比如我们的身高，你可以说你身高在 $175$至$185$，继续细分下去也是可以的，你甚至可以说你的身高在 $175.003$ 至 $182.231$ 甚至继续下分下去也没可以的，这就被称为是连续值。

1.2 离散值

🚩离散值就是单个孤立的点，比如我国共计34个省级行政区，我们绝不可以说成我国共计34.3个省级行政区，或者是33.6个省级行政区，必须是 34 整个，这就是离散值。

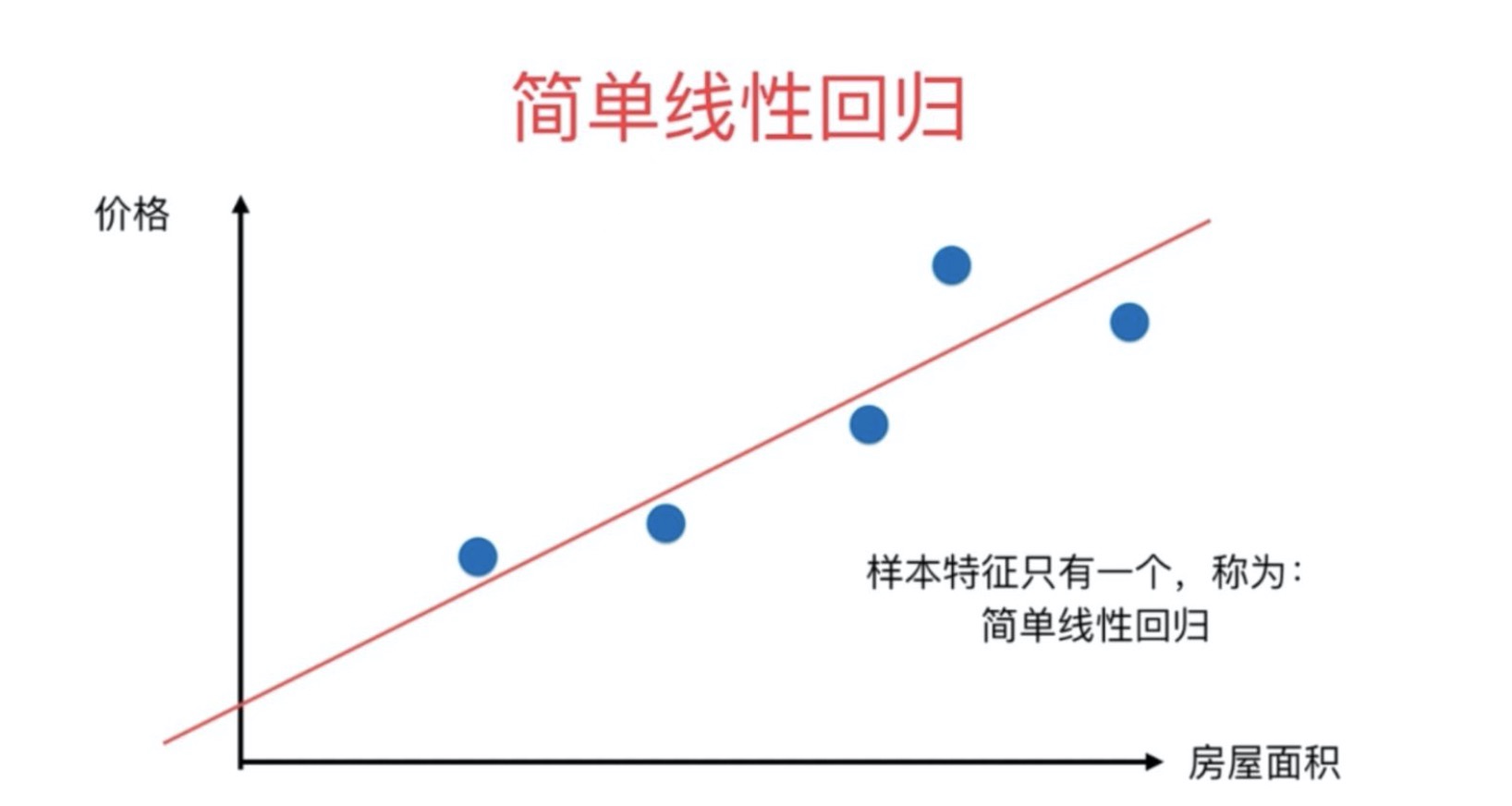
1.3 简单线性回归

🚩什么是算法？研究算法说白了还是在研究公式，简单线性回归属于一个算法，它所对应的公式：$y=wx+b$，这个公式中，$y$ 是目标变量即未来要预测的值，$x$ 是影响 $y$ 的因素，$w,b$ 是公式上的参数即要求的模型。其实 $b$ 就是咱们的截距，$w$ 就是斜率嘛！ 所以很明显如果模型求出来了，未来影响 $y$ 值的未知数就是一个 $x$ 值，也可以说影响 $y$ 值 的因素只有一个，所以这是就叫简单线性回归的原因，如下图所表示的直线，就是一个简单线性回归的意思：

1.4 基本名词的定义

$Actualvalue$:真实值，一般使用 $y$ 表示。

$Predictedvalue$:预测值，是把已知的 $x$ 带入到公式里面和猜出来的参数 $w,b$ 计算得到的，一般使用 $\hat{y}$ 表示。

$Error$:误差，预测值和真实值的差距，一般使用 $\epsilon$ 表示

最优解:尽可能的找到一个模型使得整体的误差最小，整体的误差通常叫做损失 $Loss$

$Loss$:整体的误差，$Loss$ 通过损失函数 $Loss$ $function$ 计算得到。

1.5 多元线性回归

🚩多元线性回归无非就是比简单线性回归变得： 多元，所谓多元，就是在某些情况下，影响结果 $y$ 的因素不止有一个，比如我们在预测股票的时候，国家的政策起到影响作用，国民的经济也是影响因素，甚至他国的经济政策也会影响到我们，等等等等有诸多原因，为此，仅仅一个变量 $x$ 就显得不够用了，这时，我们的 $x$ 就从 $1$ 个变成了 $n$ 个：$X_1$…$X_n$， 同时简单线性回归的公式也就不在适用了。多元线性回归公式如下：
$\hat{y}=w_1{X}_1+w_2{X}_2+\dots \dots +w_n{X}_n+b$

b是截距，也可以使用$w_0$来表示

$\hat{y}=w_1{X}_1+w_2{X}_2+\dots \dots +w_n{X}_n+w_0$

$\hat{y}=w_1{X}_1+w_2{X}_2+\dots \dots +w_n{X}_n+w_0\ast 1$

使用向量来表示，$X$表示所有的变量，是一维向量；$w$ 表示所有的系数（包含$w_0$），是一维向量，根据向量乘法规律，可以这么写：$\hat{y}=W^{T}X$

$$\hat{y}=|\begin{array}{c}{w}_1\\ w_2\\ ...\\ w_n\\ w_0\end{array}$$

多元线性回归的计算公式是怎样的？

多元线性回归公式推导及R语言实现

什么是线性回归方程？

一元线性回归模型和一元线性回归方程之间的区别

线性回归和线性回归方程是怎样的呢？

为啥要在多元回归方程中加入误差项