什么是线性回归方程？

Posted 2023-05-17

线性回归方程属于高中数学必修三，第二章，统计，属于回归分析，主要是介绍变量间的相互关系。

线性回归方程在全国卷是必考题，另外江苏，浙江，天津以及北京也会考线性规划。把公式的X、Y弄明白，然后在做相关的练习，这样做就会很快明白了。

线性回归方程的作用：

机器学习中常常用来解决相关性分析的问题，这里我们建立一个简单的数据集，这个数据集是关于学习时间和所得分数的相关性分析。机器学习的本质其实就是通过训练集建立一个模型，而后可以通过这个模型实现对于特征的识别，得出结果标签，而这个模型可以是多种多样的，简单线性回归模型只是其中的最基础最简单的一种模型。

参考技术A 线性回归方程是利用数理统计中的回归分析，来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一。线性回归也是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。按自变量个数可分为一元线性回归分析方程和多元线性回归分析方程。方法是通过对比残差，找到残差（线性方程预测值与真实值之差）最小的一个线性回归方程并作为预测方程。

机器学习线性回归的损失和优化

线性回归的损失和优化

• 线性回归的损失和优化
• 1. 损失函数
• 2. 优化算法
• • 2.1 正规方程
  • • 2.1.1 什么是正规方程
    • 2.1.2 正规方程求解举例
    • 2.1.3 正规方程的推导
    • • 推导方式一
      • 推导方式二
  • 2.2 梯度下降(Gradient Descent)
  • • 2.2.1 什么是梯度下降
    • 2.2.2 梯度的概念
    • 2.2.3 梯度下降举例
    • 2.2.4 梯度下降（Gradient Descent）公式
• 3. 梯度下降和正规方程的对比
• • 3.1 算法选择依据
• 4. 小结

线性回归的损失和优化

学习目标

• 知道线性回归中损失函数
• 知道使用正规方程对损失函数优化的过程
• 知道使用梯度下降法对损失函数优化的过程

假设刚才的房子例子，真实的数据之间存在这样的关系：

真实关系：真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

那么现在呢，我们随意指定一个关系（猜测）

随机指定关系：预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率

请问这样的话，会发生什么？真实结果与我们预测的结果之间是不是存在一定的误差呢？类似这个样子：

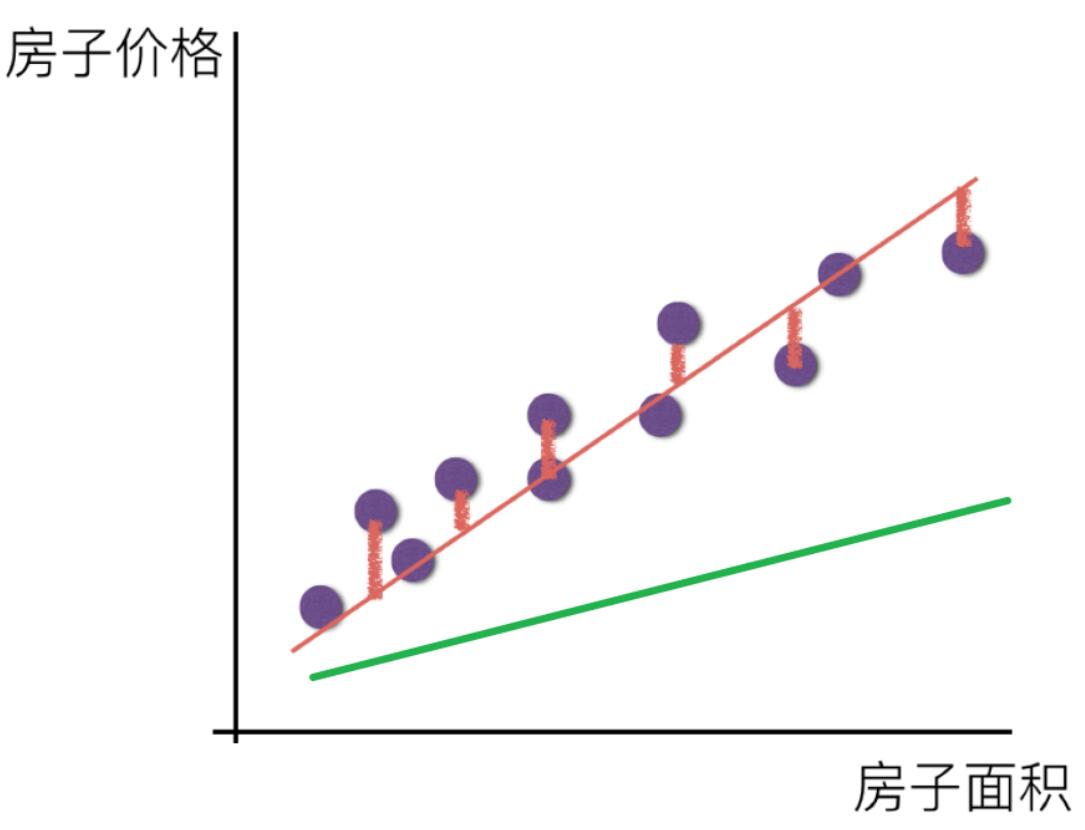
既然存在这个误差，那我们就将这个误差给衡量出来

1. 损失函数

总损失定义为：

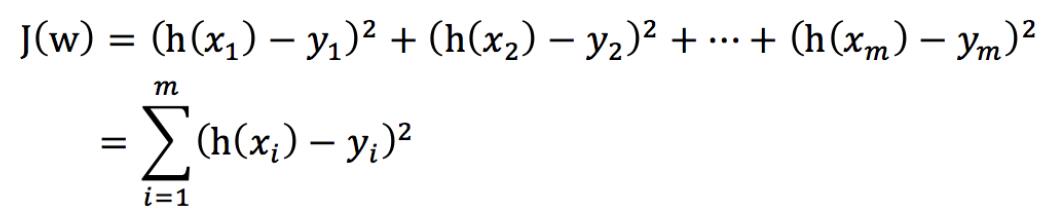
• yi为第i个训练样本的真实值
• h(xi)为第i个训练样本特征值组合预测函数
• 又称最小二乘法

如何去减少这个损失，使我们预测的更加准确些？既然存在了这个损失，我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实是数学当中的求导功能）回归的总损失！！！

2. 优化算法

如何去求模型当中的W，使得损失最小？（目的是找到最小损失对应的W值）

• 线性回归经常使用的两种优化算法

  • 正规方程
  • 梯度下降法

2.1 正规方程

2.1.1 什么是正规方程

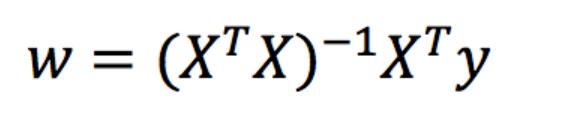
理解：X为特征值矩阵，y为目标值矩阵。直接求到最好的结果
缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

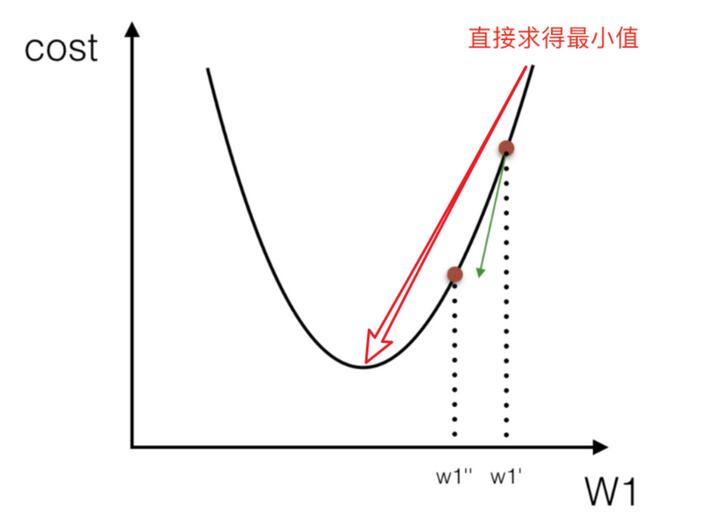
2.1.2 正规方程求解举例

以下表数据为例：

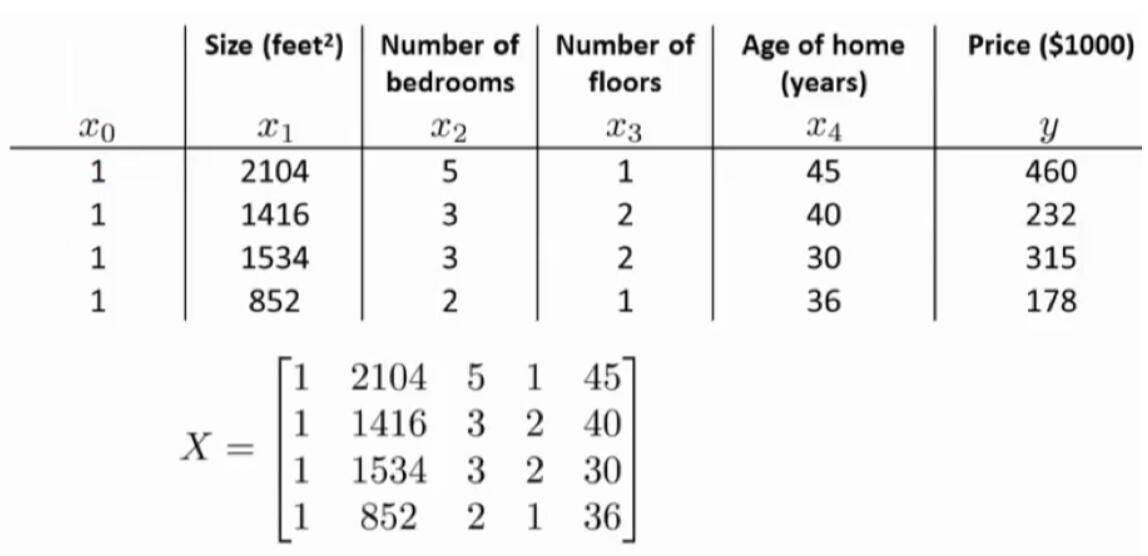
即：

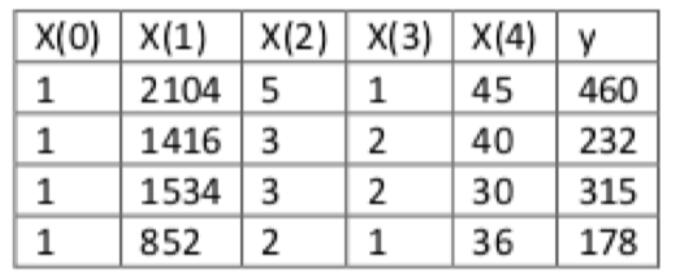
运用正规方程方法求解参数：

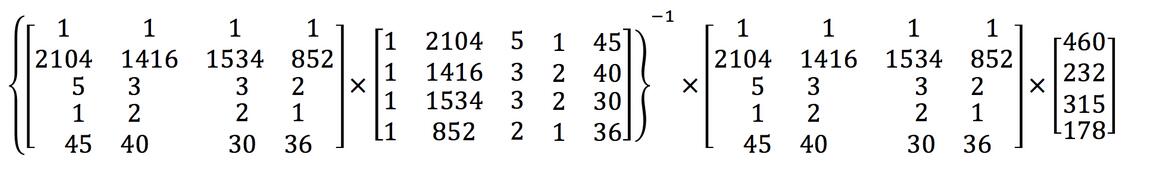
2.1.3 正规方程的推导

推导方式一

把该损失函数转换成矩阵写法：

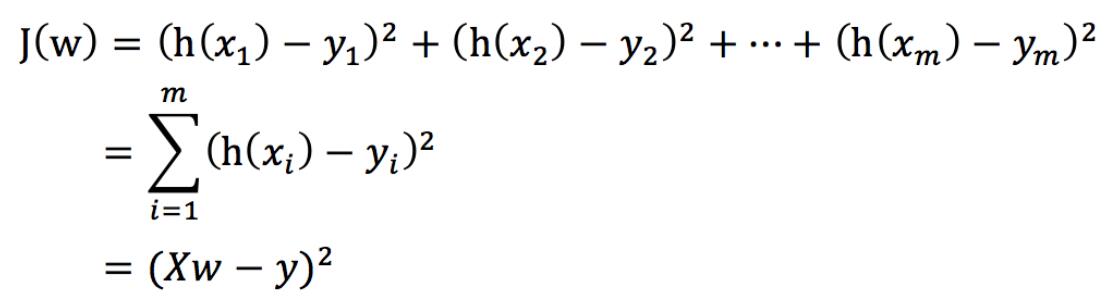
其中y是真实值矩阵，X是特征值矩阵，w是权重矩阵

对其求解关于w的最小值，起止y,X 均已知二次函数直接求导，导数为零的位置，即为最小值。

求导：

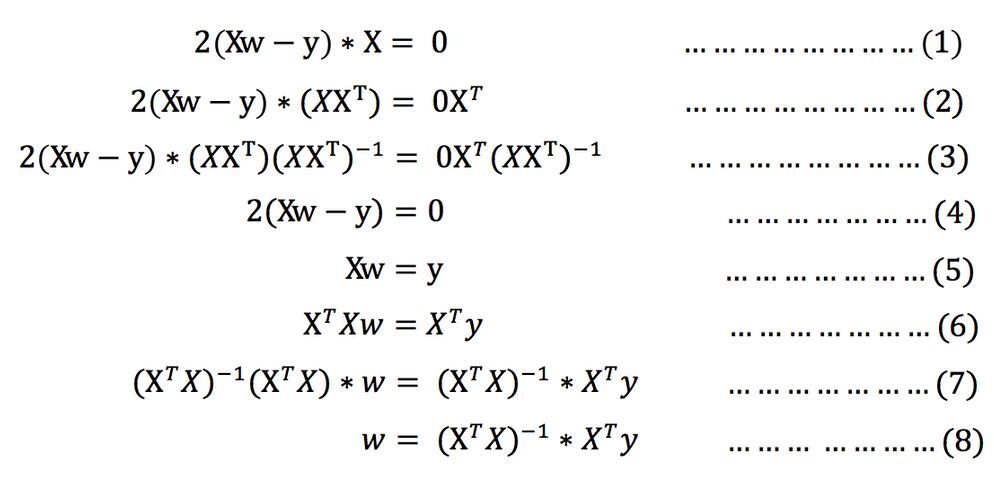
注：式(1)到式(2)推导过程中, X是一个m行n列的矩阵，并不能保证其有逆矩阵，但是右乘XT把其变成一个方阵，保证其有逆矩阵。

式(5)到式(6)推导过程中，和上类似。

推导方式二

损失表示方式

总损失定义为：

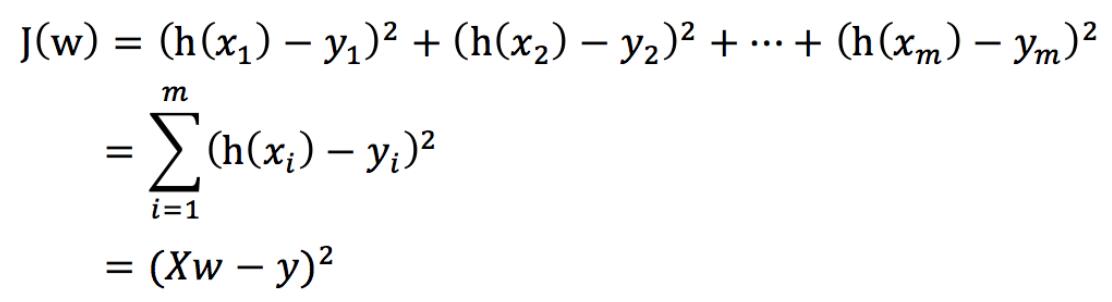
• yi为第i个训练样本的真实值
• h(xi)为第i个训练样本特征值组合预测函数
• 又称最小二乘法

另一种推导方式

把损失函数分开书写：

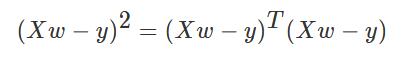
对展开上式进行求导：

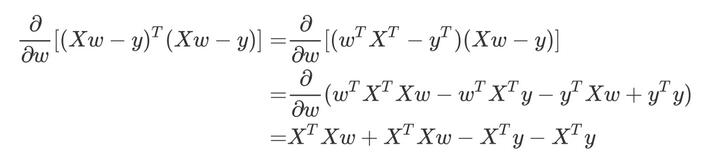
需要求得求导函数的极小值，即上式求导结果为0，经过化解，得结果为：

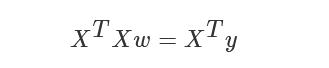
经过化解为：

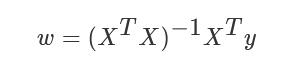
补充：需要用到的矩阵求导公式：

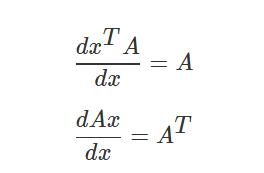
2.2 梯度下降(Gradient Descent)

2.2.1 什么是梯度下降

梯度下降法的基本思想可以类比为一个下山的过程。

假设这样一个场景：

一个人被困在山上，需要从山上下来(i.e. 找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。

因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。

具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，（同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走）。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

梯度下降的基本过程就和下山的场景很类似。

首先，我们有一个可微分的函数。这个函数就代表着一座山。

我们的目标就是找到这个函数的最小值，也就是山底。

根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数值变化最快的方向。 所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。

2.2.2 梯度的概念

梯度是微积分中一个很重要的概念

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率；

​ 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向；

这也就说明了为什么我们需要千方百计的求取梯度！我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的反方向一直走，就能走到局部的最低点！

2.2.3 梯度下降举例

1.单变量函数的梯度下降

我们开始进行梯度下降的迭代计算过程:

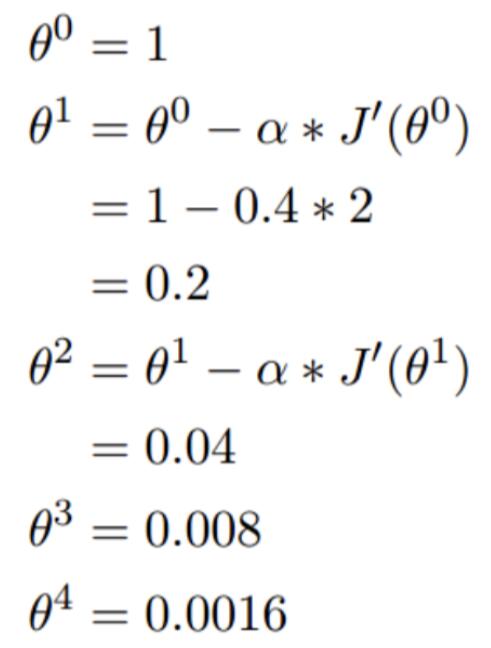
如图，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底。

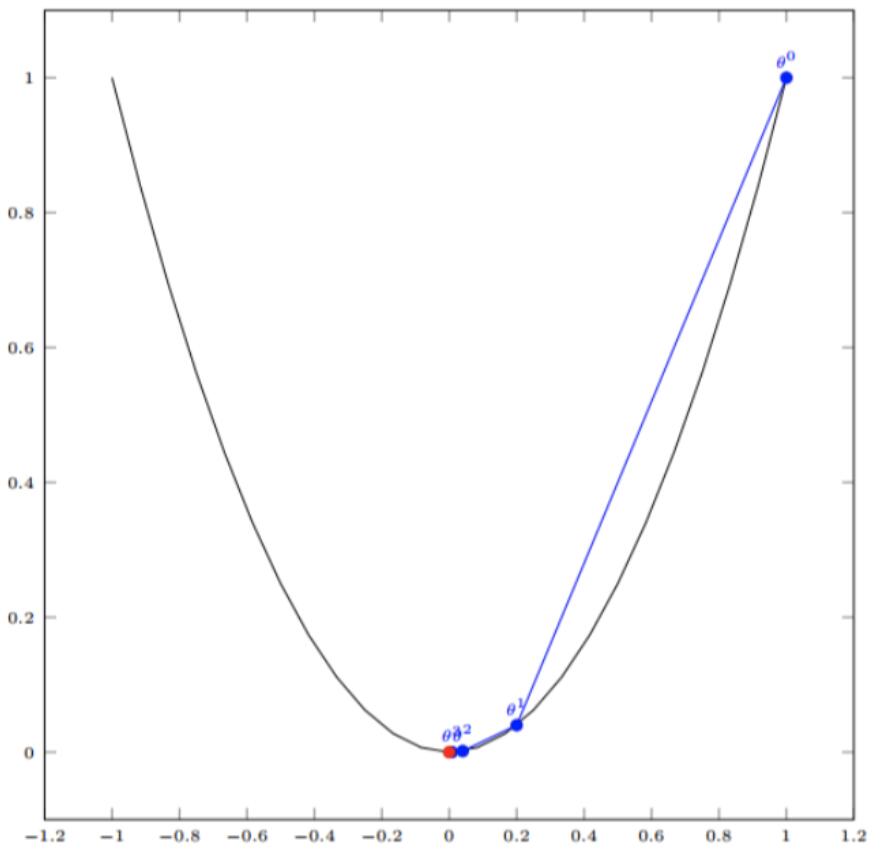
2.多变量函数的梯度下降

进行多次迭代:

我们发现，已经基本靠近函数的最小值点

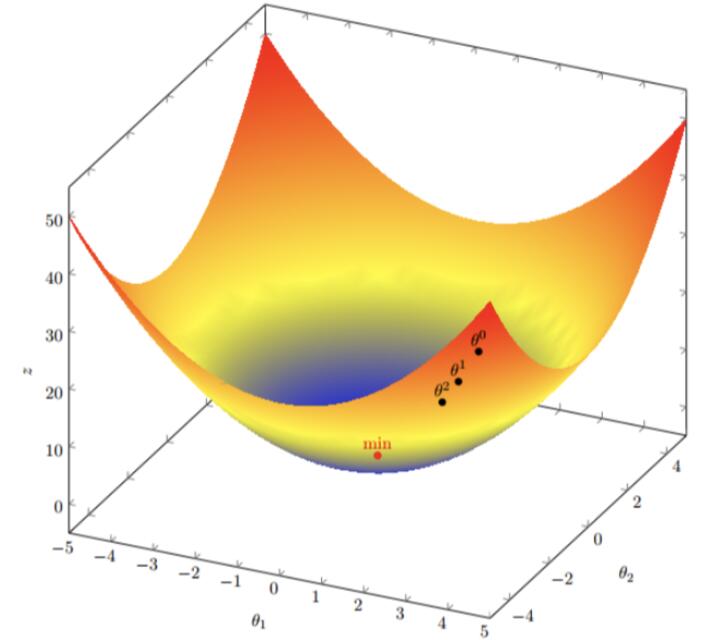
2.2.4 梯度下降（Gradient Descent）公式

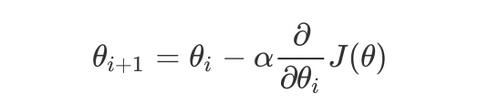
1) α是什么含义？

α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大扯着蛋，哈哈，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

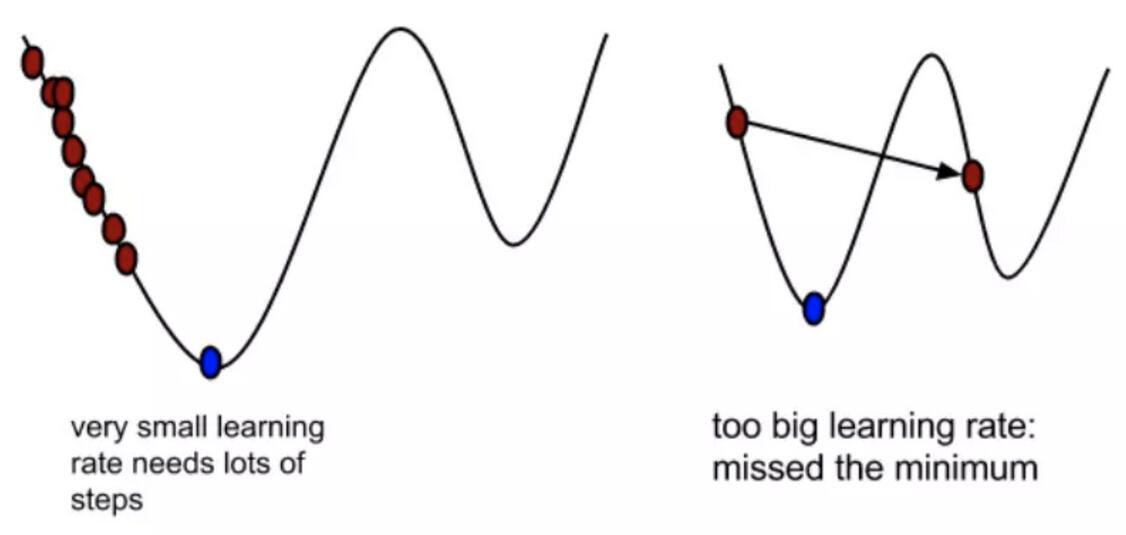
2) 为什么梯度要乘以一个负号？

梯度前加一个负号，就意味着朝着梯度相反的方向前进！我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号

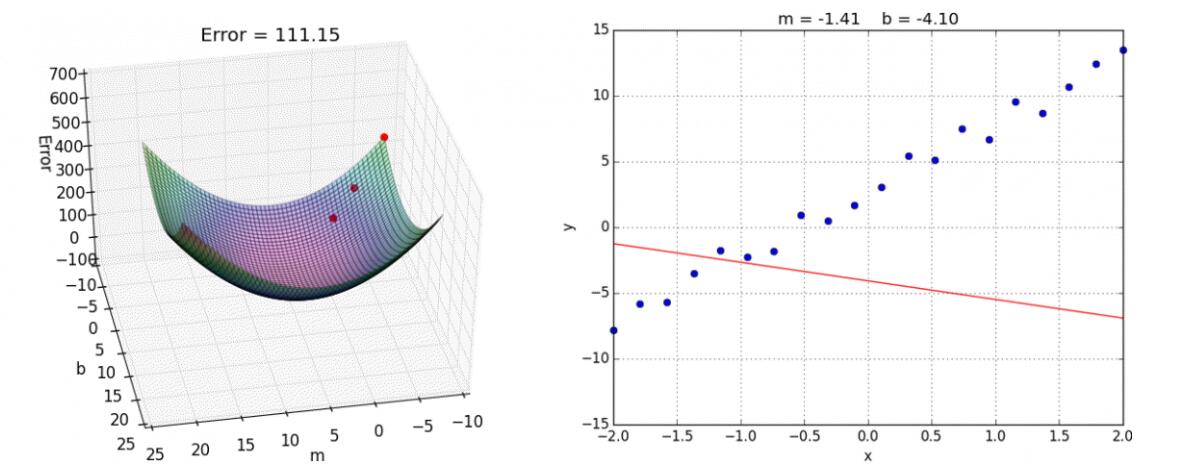
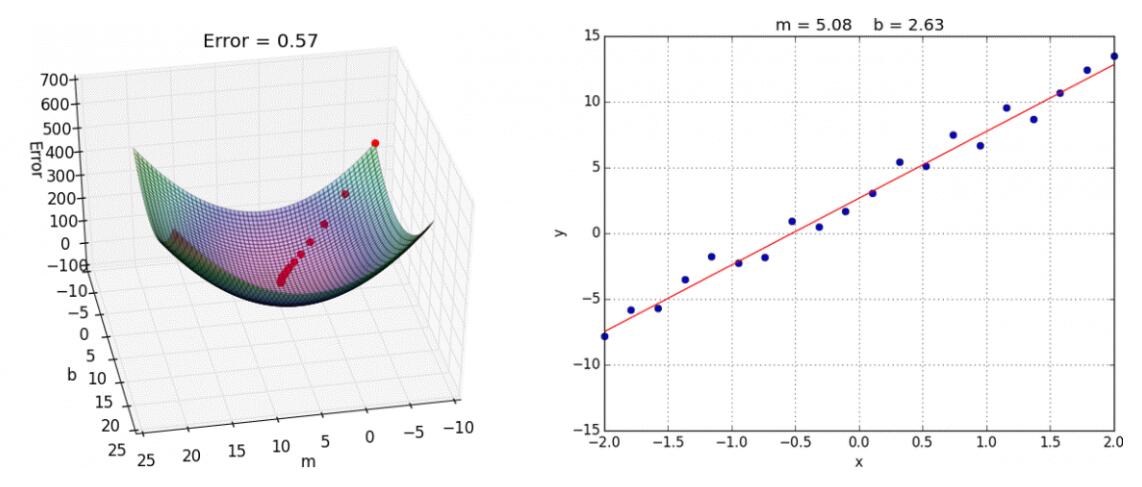
我们通过两个图更好理解梯度下降的过程

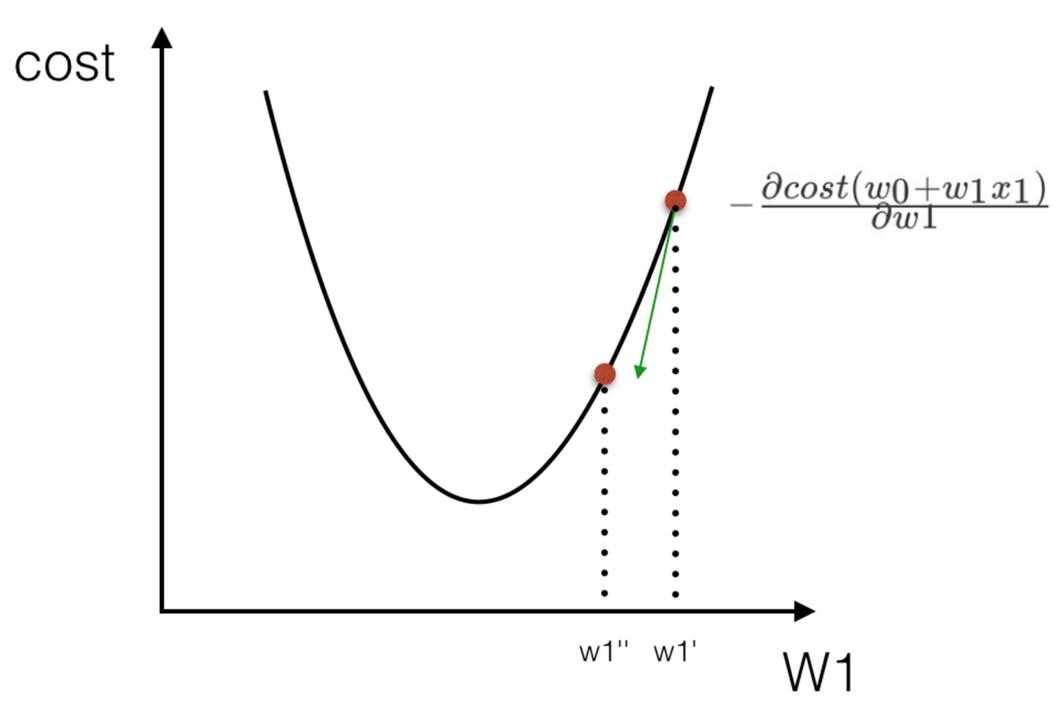
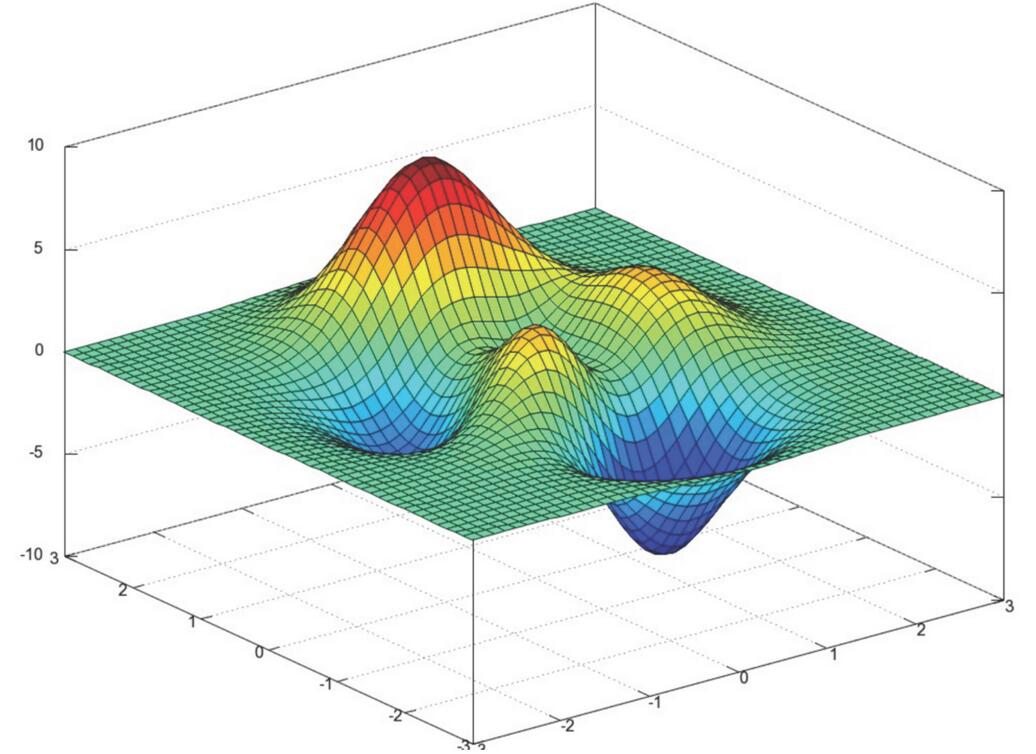
所以有了梯度下降这样一个优化算法，回归就有了"自动学习"的能力

• 优化动态图演示

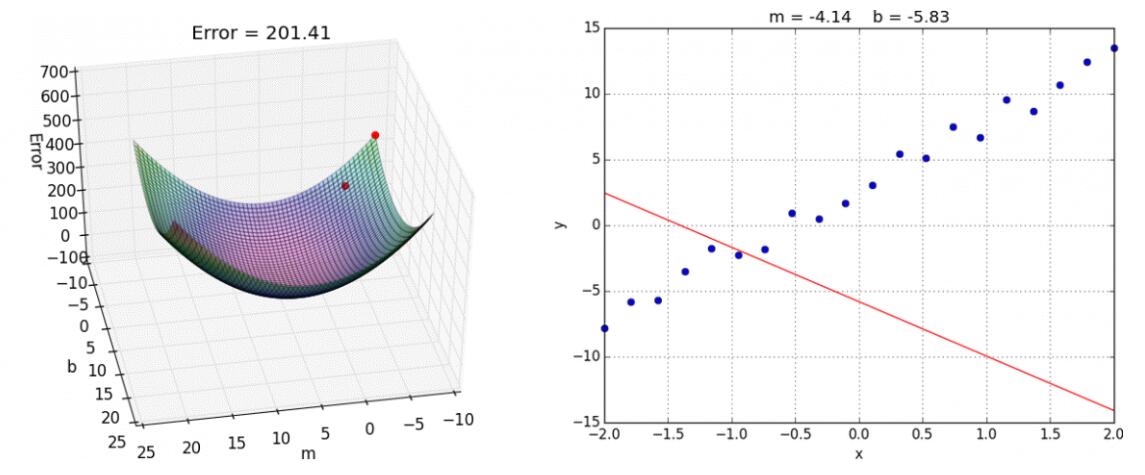
3. 梯度下降和正规方程的对比

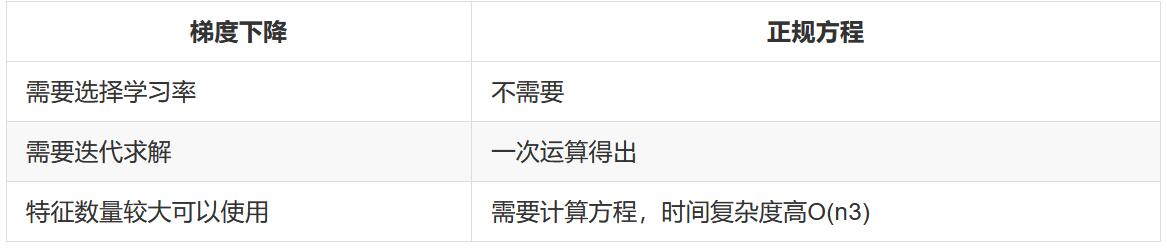
3.1 算法选择依据

• 小规模数据：
  • 正规方程：LinearRegression(不能解决拟合问题)
  • 岭回归
• 大规模数据：
  • 梯度下降法：SGDRegressor

4. 小结

• 损失函数
  • 最小二乘法
• 线性回归优化方法
  • 正规方程
  • 梯度下降法
• 正规方程 – 一蹴而就
  • 利用矩阵的逆,转置进行一步求解
  • 只是适合样本和特征比较少的情况
• 梯度下降法 — 循序渐进
  • 梯度的概念
    • 单变量 – 切线
    • 多变量 – 向量
  • 梯度下降法中关注的两个参数
    • α – 就是步长
      • 步长太小 – 下山太慢
      • 步长太大 – 容易跳过极小值点(*)
    • 为什么梯度要加一个负号
      • 梯度方向是上升最快方向,负号就是下降最快方向
• 梯度下降法和正规方程选择依据
  • 小规模数据：
    正规方程：LinearRegression(不能解决拟合问题)
    岭回归
  • 大规模数据：
    梯度下降法：SGDRegressor