UnityAPI.Quaternion四元数

Posted 2023-05-12

参考技术A Quaternion类

Quaternion类又称四元数，由x, y, z, w 4个分量组成，属于struct类型。

Unity中用其存储和表示对象的旋转角度

Quaternion的变换较为复杂，对于GameObject一般的旋转及移动，可用Transform中相关方法实现

A、Quaternion类实例属性

1、eulerAngles

public Vector3 eulerAngless get; set;

返回或设置Quaternion实例对应的欧拉角

对应GameObject对象的Transform进行欧拉角的变换次序是，先绕Z轴旋转相应角度，再绕X、Y轴旋转相应角度，不同的旋转次序得到的最终最终状态是不同的

对GameObject对象的旋转角进行赋值的方式通常有两种，一种是将Quaternion实例赋值给transform的rotation，第二种是将三维向量代表的欧拉角直接赋值给transform的eulerAngles

//rotations.eulerAngles=new Vector3(0.0f, speed*Time.time, 0.0f);

//A.rotation=rotations;

//eulerAngle=new Vector3(0.0f, speed*Time.time, 0.0f);

//B.eulerAngles=eulerAngle;

B、Quaternion类实例方法

1、SetFromToRotation

public void SetFromToRotation(Vector3 fromDirection, Vector3 toDirection);

创建一个从fromDirection到toDirection的rotation

Quaternion q1=Quaternion.identity;

q1.SetFromToRotation(v1,v2);

transform.rotation=q1;

相当于将GameObject对象进行如下变换，将GameObject对象自身坐标系的x,y,z轴方向和世界坐标系的x,y,z轴方向一致，然后将GameObject对象自身坐标系中向量v1指向的方向旋转到v2方向

不可直接使用transform.rotation.SetFromToRotation(v1,v2)方式进行设置，只能将实例化的Quaternion赋值给transfrom.rotation

2、SetLookRotation

public void SetLookRotation(Vector3 view);

Public void SetLookRotation(Vector3 view, Vector3 up);

对一个Quaternion实例的朝向进行设置

同样不能直接赋值，需要首先实例化一个Quaternion，然后调用方法后，赋值给transfrom.rotation

transform.forward方向与v1方向相同

transform.right垂直于由Vector3.zero, v1和v2三点构成的平面

v2用来决定transform.up的朝向，选取方式使得transform.up的方向和v2方向的夹角小于或等于90度

v1为Vector3.zero时，方法失效

3、ToAngleAxis

public void ToAngleAxis(out float angle, out Vector3 axis);

angle为旋转角，axis为轴向量

将Quaternion实例转换为角轴表示，即要将GameObject对象的rotation从Quaternion.Identity状态变换到当前状态，只需将GameObject对象绕着axis的轴向（指世界坐标系中）旋转angle角度即可。

此方法通常和静态方法AngleAxis（float angle, Vector3 axis）联合使用，使得一个物体的rotation始终和另一个物体的rotation保持一致

C、Quaternion类静态方法

1、Angle

public static float Angle(Quaternion a, Quaternion b);

用于返回从参数a到参数b变换的夹角，即GameObject对象从状态a转换到状态b时需要旋转的最小夹角

2、Dot

public static float Dot(Quaternion a, Quaternion b);

求参数a, b的点乘

q1=(x1,y1,z1,w1)

q2=(x2,y2,z2,w2)

float f=Quaternion.Dot(q1,q2)

f=x1*x2+y1*y2+z1*z2+w1*w2，f的范围为[-1,1]

当f=1时，他们的rotation相等

当f=-1时，其中一个rotation比另一个多旋转乐360度

3、Euler

public static Quaternion Euler(Vector3 euler);

public static Quaternion Euler(float x, float y, float z);

此方法用于返回欧拉角Vector3(x,y,z)对应的四元数Quaternion实例

四元数(qx,qy,qz,qw)与欧拉角(ex,ey,ez)的对应关系：

ex=ex*PIover180/2.0f;

ey=ey*PIover180/2.0f;

ez=ez*PIlover180/2.0f;

qx=sin(ex)cos(ey)cos(ez)+cos(ex)sin(ey)sin(ez);

qy=cos(ex)sin(ey)cos(ez)-sin(ex)cos(ey)sin(ez);

qz=cos(ex)cos(ey)sin(ez)-sin(ex)sin(ey)cos(ez);

qw=cos(ex)cos(ey)cos(ez)+sin(ex)sin(ey)sin(ez);

4、FromToRotation

public static Quaternion FromToRotation(Vector3 fromDirection, Vector3 toDirection);

用来创建一个从参数fromDirection到toDirection的Quaternion变换

功能和实例方法SetFromToRotation相同，只是用法上有些不同

5、Inverse

public static Quaternion Inverse(Quaternion rotation);

用于返回参数rotation的逆向Quaternion值

例如实例rotation=(x,y,z,w)

Inverse(rotatiom)=(-x, -y, -z, w)

效果上，rotation.eulerAngles=(a, b, c)

transform.rotation=Inverse(rotation)相当于transform依次绕自身坐标系的z轴、x轴、y轴分别旋转-c度，-a度和-b度

但由于时局部坐标系内的变换，最后transform的欧拉角的各个分量值并不一定等于-a，-b，-c

6、Lerp

public static Quaternion Lerp(Quaternion from, Quaternion to, float t);

用于返回从参数from到to的线性插值

当t<=0，返回from，当参数t>=1，返回to。执行速度比slerp方法快，一般可代替Slerp方法

7、LookRotation

public static Quaternion LookRotation(Vector3 forward);

public static Quaternion LookRotation(Vector3 forward, Vector3 upwards);

forward为返回Quaternion的forward朝向

用于返回一个Quaternion实例，使GameObject对象的z轴朝向参数forward方向

与方法SetLookRotation功能相同，只是用法上有些不同

8、RotateTowards

public static Quaternion RotateTowards(Quaternion from, Quaternion to, float maxDegreesDelta);

from为起始，to为结束，参数maxDegreesDelta为每帧最大角度值

用于返回从参数from到参数to的插值，且返回值的最大角度不超过maxDegreesDelta

功能与Slerp相似，只是maxDegreesDelta指角度值，而不是插值系数，<0时，将沿to到from方向插值计算

9、Slerp

public static Quaternion Slerp(Quaternion from, Quaternion to, float t);

用于返回从参数from到to的球面插值

参数t<=0时返回值为from，参数t>=1时返回值为to，一般情况下可用Lerp方法代替

四元数运动学笔记旋转的雅克比矩阵

1.相对于旋转向量的雅克比
2.相对于四元数的雅克比
2.1相关公式
2.2推导雅克比

1.相对于旋转向量的雅克比

• 这里在全局系下利用左扰动进行推导：
  $\frac{\mathrm{\partial }{a}^{{}^{\prime }}}{\mathrm{\partial }\theta }=\frac{\mathrm{\partial }Ra}{\mathrm{\partial }\theta }$

  

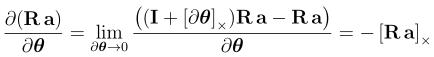
2.相对于四元数的雅克比

2.1相关公式

• 三叉积公式:

  

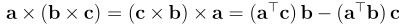
• 纯实部的四元数和四元数相乘,这里$q_w$是实数
  
  $$[q_w,0_3{]}^T\otimes q=q_w{q}_1\otimes q=q_{w}q$$
• 两个纯虚四元数相乘：

  

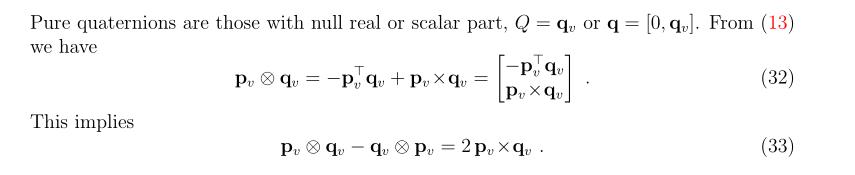
2.2推导雅克比

• 由以上三个公式可以得到以下公式的推导，其中这里的$w,v,a$在涉及到四元数相乘的情况时，都是四元数的表示形式（纯实部四元数和纯虚部四元数），其他情况下则是正常的标量和三维向量。

  

• 旋转过程相对于四元数的雅克比

  

null