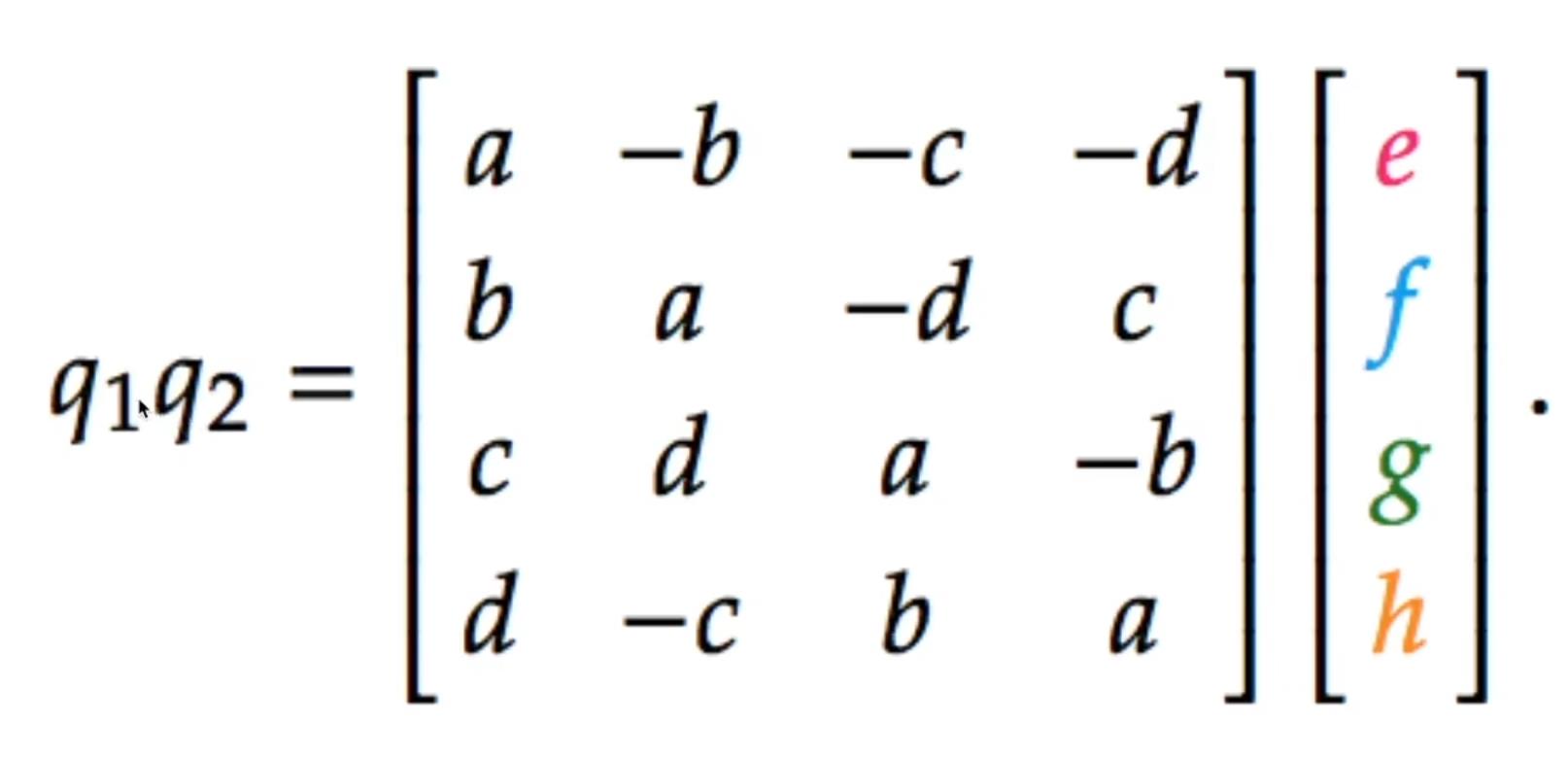四元数法

Posted 2023-04-01 zylyehuo

四元数法

概念

四元数是一种用于表示旋转和方向的数学对象，它由一个实部和三个虚部组成。四元数可以用来替代旋转矩阵，在计算机图形学、机器人学、物理学等领域有广泛的应用。

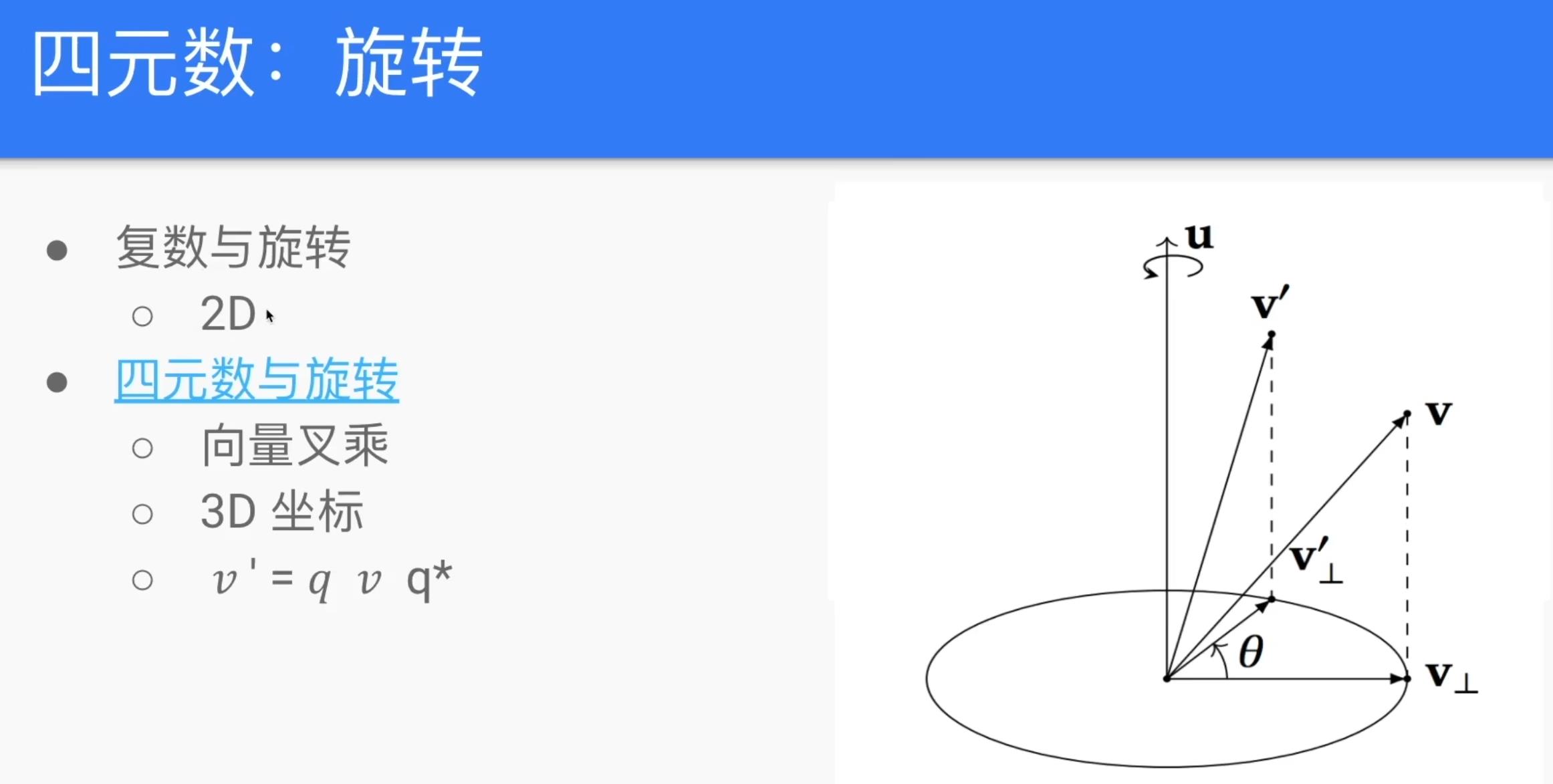
四元数的一般形式为：q = a + bi + cj + dk，其中a,b,c,d为实数，i,j,k为虚数单位，满足i^2=j2=k^2=ijk=-1。四元数的实部a表示旋转的余弦值，虚部bi+cj+dk表示旋转的轴向及其角度。

四元数法是一种使用四元数进行运动学计算的方法，包括旋转、位移、缩放等变换。与欧拉角相比，四元数法有更好的数值稳定性和计算效率，避免了万向锁问题。在3D游戏和动画领域，四元数法也是常用的动画插值方法之一，可以实现流畅的动画效果。

• 
• 
• 
• 
• 

举例

假设有一个物体在三维空间中，需要将其绕着一个轴旋转一定的角度，可以使用四元数来表示这个旋转变换。首先需要构造表示旋转的四元数：

首先需要确定旋转的轴向，可以将轴向向量归一化，得到单位向量 u = [ux, uy, uz]。
根据旋转角度 theta，计算旋转的复数部分 c = cos(theta/2)，以及旋转的虚数部分 s = sin(theta/2)。
构造四元数 q = c + su = [c, sux, suy, s*uz]。
通过构造的四元数 q，可以对物体进行旋转变换，具体地，对于三维空间中的一个点 p = [px, py, pz]，可以进行如下变换：

构造点 p 的四元数 p0 = [0, px, py, pz]，即将点 p 表示成四元数的形式，实部为 0。
计算旋转后的四元数 p1 = qp0q，其中 q 表示 q 的共轭四元数，即 q 的实部不变，虚部取相反数。
将旋转后的四元数 p1 表示成点的形式，即 p\' = [p1x, p1y, p1z]，其中 p1x, p1y, p1z 分别对应 p1 的三个虚数部分。
这样就完成了对点 p 的旋转变换。可以使用四元数法进行多个旋转的叠加，也可以使用四元数法进行插值，实现平滑的动画效果。

matlab练习程序（对应点集配准的四元数法）

这个算是ICP算法中的一个关键步骤，单独拿出来看一下。

算法流程如下：

1.首先得到同名点集P和X。

2.计算P和X的均值up和ux。

3.由P和X构造协方差矩阵sigma。

4.由协方差矩阵sigma构造4*4对称矩阵Q。

5.计算Q的特征值与特征向量。其中Q最大特征值对应的特征向量即为最佳旋转向量q。

6.通过四元数q得到旋转矩阵R。

7.根据R计算最佳平移向量qr。

具体公式我就不贴图了，可以参考这篇“ICP算法在点云配准中的应用”论文的3.1节。

处理效果如下：

原始点集：

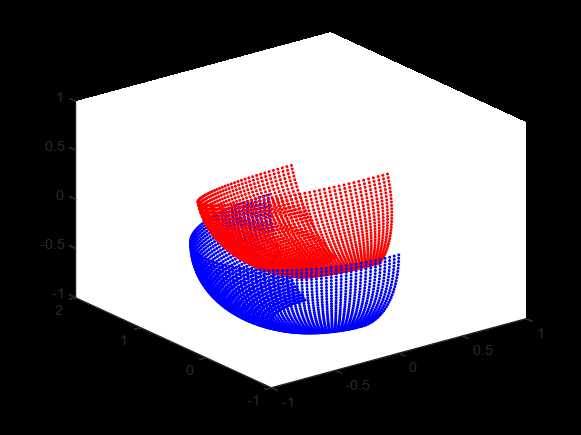
其中蓝点为原始点集，红点为旋转平移后的点集。

配准后点集：

 

 

计算得到的旋转平移矩阵，通过对蓝点集进行转换得到绿点集，比较红点集与绿点集是否基本一致。

matlab代码如下：

clear all;
close all;
clc;

%生成原始点集
X=[];Y=[];Z=[];
for i=-180:2:180
    for j=-90:2:90
        x = i * pi / 180.0;
        y = j * pi / 180.0;   
        X =[X,cos(y) * cos(x)];
        Y =[Y,sin(y) * cos(x)];
        Z =[Z,sin(x)]; 
    end
end
P=[X(1:3000)‘ Y(1:3000)‘ Z(1:3000)‘];

%生成变换后点集
i=0.5;j=0.3;k=0.7;
Rx=[1 0 0;0 cos(i) -sin(i); 0 sin(i) cos(i)];
Ry=[cos(j) 0 sin(j);0 1 0;-sin(j) 0 cos(j)];
Rz=[cos(k) -sin(k) 0;sin(k) cos(k) 0;0 0 1];
R=Rx*Ry*Rz;
X=P*R + [0.2,0.3,0.4];

plot3(P(:,1),P(:,2),P(:,3),‘b.‘);
hold on;
plot3(X(:,1),X(:,2),X(:,3),‘r.‘);

%计算点集均值
up = mean(P);
ux = mean(X);

P1=P-up;
X1=X-ux;

%计算点集协方差
sigma=P1‘*X1/(length(X1));
sigma_mi = sigma - sigma‘;
M=sigma+sigma‘-trace(sigma)*[1,0,0;0,1,0;0,0,1];

%由协方差构造4*4对称矩阵
Q=[trace(sigma) sigma_mi(2,3) sigma_mi(3,1) sigma_mi(1,2);
   sigma_mi(2,3) M(1,1) M(1,2) M(1,3);
   sigma_mi(3,1) M(2,1) M(2,2) M(2,3);
   sigma_mi(1,2) M(3,1) M(3,2) M(3,3)];

%计算特征值与特征向量
[x,y] = eig(Q);
e = diag(y);

%计算最大特征值对应的特征向量
lamda=max(e);
for i=1:length(Q)
    if lamda==e(i)
        break;
    end
end
q=x(:,i);

q0=q(1);q1=q(2);q2=q(3);q3=q(4);

%由四元数构造旋转矩阵
RR=[q0^2+q1^2-q2^2-q3^2 ,2*(q1*q2-q0*q3), 2*(q1*q3+q0*q2);
   2*(q1*q2+q0*q3), q0^2-q1^2+q2^2-q3^2, 2*(q2*q3-q0*q1);
   2*(q1*q3-q0*q2), 2*(q2*q3+q0*q1), q0^2-q1^2-q2^2+q3^2];

%计算平移向量
qr=ux-up*RR‘;

%验证旋转矩阵与平移向量正确性
Pre = P*RR‘+qr;

figure;
plot3(P(:,1),P(:,2),P(:,3),‘b.‘);
hold on;
plot3(X(:,1),X(:,2),X(:,3),‘r.‘);

plot3(Pre(:,1),Pre(:,2),Pre(:,3),‘go‘);