谁知道每行每列及两条对角线的三个数的和都相等

Posted 2023-04-12

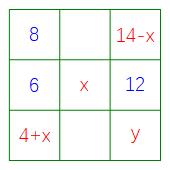
如图所示，设中间的数为x，则每行每列及两条对角线上的数字之和为6+x+12=18+x，

则左下角的数字为(18+x)-8-6=4+x，进而可知右上角的数字为14-x，

设右下角的数字为y，则有8+x+y=(14-x)+12+y，解得x=9，所以得解：

参考技术A

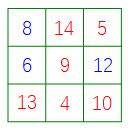
根据洛书九宫图提示，不管是每列每行和对角线，两边和的二分之一必定是中间数字，那么有条件的就是(6+12)/2＝9，中间是9，每列每行与对角线的和都是6+9+12＝27，所以看图

追答

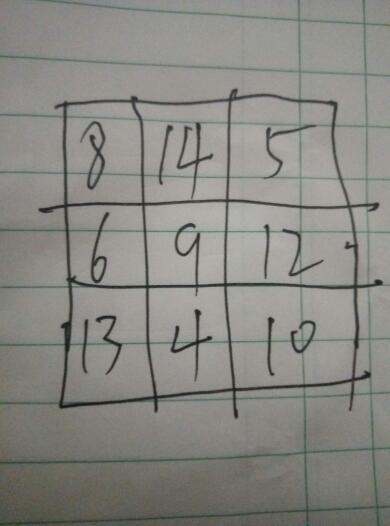
更正一下，不是每行每列，是跟中宫成行成列及对角线的中宫两边和的一半必定等于中宫数字

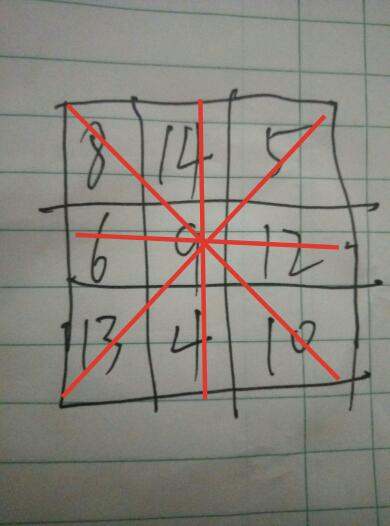
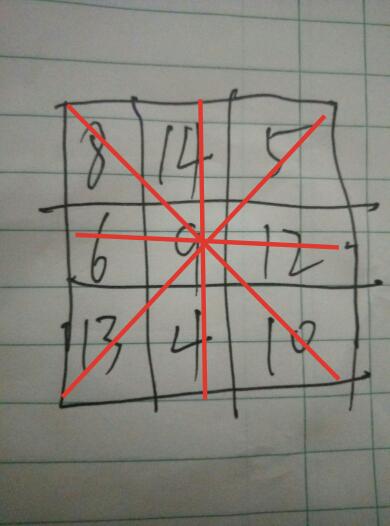
红线上的三个数，两边数和的一半等于中间数

本回答被提问者采纳

[解题报告][搜索+剪枝技巧]幻方

【Description】
请解决一个 N 阶幻方。(N=3或4)
为了凑够 15 字补一个幻方的简介好了。给定 N*N 个数，把它们填入 N*N 的方格中，使每
行每列和两个斜对角线里数的和都相等。
【Input】
第一行一个正整数 N
第二行 N*N 个整数，代表要填入幻方中的数
【Output】
N 行每行 N 个整数，用空格隔开，代表填好的幻方。
如果有多组解，输出任意一组即可。
保证有解。
【Sample Input1】
3
9 9 9 9 9 9 9 9 9
【Sample Output1】
9 9 9
9 9 9
9 9 9
【Sample Input2】
3
1 2 3 4 5 6 7 8 9
【Sample Output2】
2 7 6
9 5 1
4 3 8

思路:

 1.如果n=3,可以暴力枚举，复杂度为O(9!)

 2.n=4时，直接暴力4*4的话一定会挂，可以只暴力8个格子

　　　　　　　　　　# # # #

　　　　　　　　　　# 1 # 8

　　　　　　　　　　# 6 2 7

　　　　　　　　　　# 5 4 3

剪枝1:只搜8个格子（上)

剪枝2：按照一定的顺序搜索，当搜索到一些特定的格子就能推算出某个#的数值，如果#不在可用数字范围内，可以直接return

优化1:记录每个数字出现的个数，判断是否在可用范围内时直接判断个数，注意最好不要用map（似乎会消耗大量时间），可以用unordered_map或者自己离散化。

幻方和=所有数字总和/n

 

代码:

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <algorithm>
  4 #include <map>
  5 #include <ctime>
  6 #include <cstring>
  7 using namespace std;
  8 int pl[20],use[20];
  9 int n,pn,sum;
 10 int hf[5][5];
 11 int mm[20],mmct[20];
 12 int mp=0;
 13 #define covidx(x,y) (x-1)*4+(y-1)
 14 void prints()
 15 {
 16     for(int i=1; i<=n; i++)
 17         for(int j=1; j<=n; j++)
 18             {
 19                 printf("%d%c",hf[i][j],j==n?‘\n‘:‘ ‘);
 20             }
 21 }
 22 inline int getid(int a)
 23 {
 24     for(int i=0; i<mp; i++)
 25         {
 26             if(mm[i]==a) return i;
 27         }
 28     return 19;
 29 }
 30 inline int check()
 31 {
 32     int t1=0,t2=0,t3=0,t4=0;
 33     for(int i=1; i<=n; i++)
 34         {
 35             t1+=hf[i][i];
 36             t2+=hf[i][n-i+1];
 37             for(int j=1; j<=n; j++)
 38                 {
 39                     t3+=hf[i][j];
 40                     t4+=hf[j][i];
 41                 }
 42             if(t3!=t4 || t3!=sum || t4!=sum) return 0;
 43             else if(i!=n)
 44                 t3=t4=0;
 45         }
 46     if(t2!=t1) return 0;
 47     if(t3!=t2) return 0;
 48     if(t2!=sum) return 0;
 49     return 1;
 50 }
 51 void fuck3(int x,int y)
 52 {
 53 
 54     if(x==4)
 55         {
 56             if(check())
 57                 {
 58                     prints();
 59                     exit(0);
 60                 }
 61             else
 62                 return;
 63         }
 64     int tx,ty;
 65     for(int i=1; i<=pn; i++)
 66         {
 67             if(!use[i])
 68                 {
 69                     use[i]=1;
 70                     hf[x][y]=pl[i];
 71                     if(y==3)
 72                         {
 73                             ty=1;
 74                             tx=x+1;
 75                         }
 76                     else
 77                         {
 78                             ty=y+1;
 79                             tx=x;
 80                         }
 81                     fuck3(tx,ty);
 82                     use[i]=0;
 83                 }
 84         }
 85 }
 86 
 87 /*
 88  3 6 8 8
 89 #7 1 8 8
 90  7 6 2 7
 91  5 5 4 3
 92 
 93  1  2  3  4
 94  5  6  7  8
 95  9  10 11 12
 96  13 14 15 16
 97 */
 98 int xyidx[9][2]= {{-1,-1},{2,2},{3,3},{4,4},{4,3},{4,2},{3,2},{3,4},{2,4}};
 99 int deps[16][8]=
100 {
101     {1,2,3},{1,6,5},{-1,-2,-4},{8,7,3},
102     {-1,-9,-13},{0},{-5,1,8},{0},
103     {6,2,7},{0},{0},{0},
104     {5,4,3},{0},{0},{0}
105 };
106 int lin[16][4]=
107 {
108     {0},{0},{0},{3},
109     {0},{0},{4},{7},
110     {5},{2},{0},{9},
111     {0},{13},{0},{1}
112 };
113 
114 
115 
116 int prelin(int idx)
117 {
118     int i,j;
119     i=0;
120     if(idx>0)
121         idx=(xyidx[idx][0]-1)*4+xyidx[idx][1]-1;
122     else
123         idx=-idx;
124     while(lin[idx][i]!=0)
125         {
126             int cpa=lin[idx][i];
127             int x=(cpa-1)/4+1;
128             int y=(cpa-1)%4+1;
129             int nsum=0;
130             j=0;
131             cpa-=1;
132             while(deps[cpa][j]!=0)
133                 {
134                     int dalao=deps[cpa][j],x,y;
135                     if(dalao>0)
136                         {
137                             x=xyidx[dalao][0];
138                             y=xyidx[dalao][1];
139                         }
140                     else
141                         {
142                             dalao=-dalao;
143                             dalao-=1;
144                             x=dalao/4+1;
145                             y=dalao%4+1;
146                         }
147                     nsum+=hf[x][y];
148                     j++;
149                 }
150             int id;
151             if(mmct[id=getid(sum-nsum)]>0)
152                 {
153                     hf[x][y]=sum-nsum;
154                     mmct[id]--;
155                     prelin(-(covidx(x,y)));
156                 }
157             else
158                 {
159                     return 0;
160                 }
161             i++;
162         }
163     return 1;
164 }
165 void dfs4(int idx)
166 {
167     if(idx==9)
168         {
169             if(check())
170                 {
171                     prints();
172                     exit(0);
173                 }
174             else
175                 {
176                     return;
177                 }
178         }
179     //给idx填数
180     int x=xyidx[idx][0];
181     int y=xyidx[idx][1];
182     int bnaive[20];
183     memcpy(bnaive,mmct,sizeof(mmct));
184     int id;
185     for(int i=1; i<=pn; i++)
186         {
187             if(mmct[id=getid(pl[i])]>0)
188                 {
189                     mmct[id]--;
190                     hf[x][y]=pl[i];
191                     if(prelin(idx)==0)
192                         {
193                             memcpy(mmct,bnaive,sizeof(mmct));
194                             continue;
195                         }
196                     dfs4(idx+1);
197                     memcpy(mmct,bnaive,sizeof(mmct));
198                 }
199         }
200 }
201 int main()
202 {
203     //freopen("magicsquare.in","r",stdin);
204     //freopen("magicsquare.out","w",stdout);
205     scanf("%d",&n);
206     pn=n*n;
207     for(int i=1; i<=pn; i++)
208         {
209             scanf("%d",&pl[i]);
210             sum+=pl[i];
211         }
212     sort(&pl[1],&pl[pn+1]);
213     if(n==3)
214         fuck3(1,1);
215     else
216         {
217             sum/=4;
218             for(int i=1; i<=pn; i++)
219                 {
220                     int id;
221                     if((id=getid(pl[i]))==19)
222                         {
223                             mm[mp]=pl[i];
224                             mmct[mp]=1;
225                             mp++;
226                         }
227                     else
228                         {
229                             mmct[id]++;
230                         }
231                 }
232             dfs4(1);
233         }
234 }