Polygon zkEVM Binary状态机

Posted 2022-09-07 mutourend

1. 引言

前序博客有：

• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式

Binary状态机为Polygon zkEVM的六个二级状态机之一，该状态机内包含：

• executor part：sm_binary.js：负责生成execution trace，为常量多项式和隐私多项式赋值。
• 验证规则集PIL：binary.pil：定义了约束系统。

相应的test vectors见：binary_test.js：包含了所支持的各类计算的测试集。

Polygon zkEVM Binary状态机针对的是256-bit字符串的二进制运算，当前支持的二进制运算有：

Table 1: All Operations Checked by the Binary SM

$\text{Operation Name}$	$\text{Mnemonic}$	$\text{Symbol}$	$\text{BinOpCode}$
$\text{Addition}$	$\mathrm{ADD}$	$+$	$0$
$\text{Subtraction}$	$\mathrm{SUB}$	$-$	$1$
$\text{Less Than}$	$\mathrm{LT}$	$<$	$2$
$\text{Signed Less Than}$	$\mathrm{SLT}$	$<$	$3$
$\text{Equal To}$	$\mathrm{EQ}$	$=$	$4$
$\text{Bitwise AND}$	$\mathrm{AND}$	$\wedge$	$5$
$\text{Bitwise OR}$	$\mathrm{OR}$	$\vee$	$6$
$\text{Bitwise XOR}$	$\mathrm{XOR}$	$\oplus$	$7$
$\text{No Operation}$	$\mathrm{NOP}$	$\mathrm{NOP}$	$\star$

相应的运算定义可参见zkasmcom中的zkasm_parser.jison中：

    | ADD
        
            $$ =  bin: 1, binOpcode: 0
        
    | SUB
        
            $$ =  bin: 1, binOpcode: 1
        
    | LT
        
            $$ =  bin: 1, binOpcode: 2
        
    | SLT
        
            $$ =  bin: 1, binOpcode: 3
        
    | EQ
        
            $$ =  bin: 1, binOpcode: 4
        
    | AND
        
            $$ =  bin: 1, binOpcode: 5
        
    | OR
        
            $$ =  bin: 1, binOpcode: 6
        
    | XOR
        
            $$ =  bin: 1, binOpcode: 7
        

2. 将256位字符串编码为有符号位和无符号位整数

在理解以上运算规则的工作原理之前，需首先了解zkEVM是如何将256位字符串编码为signed integers和unsigned integers。

以3-bit字符串为例，相应的uint和int编码表示为：【可很容易将其扩展至256-bit字符串】【对于int表示，需注意-4和4具有相同的编码方式。】

ADD和SUB可逐bit运算，如以3-bit string 0b001和0b101（0b表示二进制）为例，逐bit add为：

• 初始$carry=0$，最低有效位相加有：$1+1+carry=1+1+0=0$，因此，下一carry值为$carr{y}^{\prime }=1$。

• 其次，将次低有效位相加，并与前一carry相加，有$0+0+carry=0+0+1=1$，此时，下一carry值为$carr{y}^{\prime }=0$。

• 最后，将最高有效位相加，并与前一carry相加，有$0+1+carry=0+1+0=1$，最终carry值为$carr{y}^{\prime }=0$。

• 最终结果为：$0b001+0b101=0b110$ with $carry=0$。

不过LT（less than）与 SLT（unsigned less than）有所不同，LT按正常顺序直接比较即可，而SLT：

• 1）若最高有效位相同，则按正常顺序直接比较，如101<110，即-3<-2。
• 2）若最高有效位不同，则顺序相反（以0为最高有效位的值更大），如110<001，即-2<1。

而AND/OR/XOR/NOT运算均为bit-wise运算，即可逐位计算，且无需考虑进位（carry）情况：

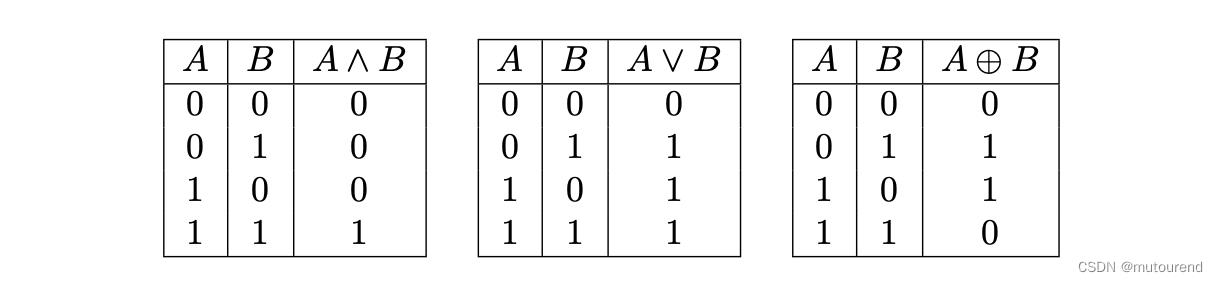
注意，zkEVM中未单独设置NOT运算符，因NOT运算可看成是与0xff…ff的XOR运算。

3. polygon zkEVM Binary状态机设计思想

polygon zkEVM Binary状态机的executor part：sm_binary.js，负责记录状态机内的每个computation trace，该computation trace可用于证明计算的正确性。
execution trace通常以256-bit字符串来表示，每个正确的execution trace必须满足相应的多项式约束，这些多项式约束定义在PIL代码文件中。

3.1 internal Byte Plookups

Binary状态机内部使用plookups of bytes来表达所有二进制运算。
在其plookups table中，包含了所有可能的input bytes和output byte组合：
$${\text{byte}}_{i{n}_0}\star {\text{byte}}_{i{n}_1}={\text{byte}}_{out},$$
其中$\star$表示所有可能的运算。
当对256-bit字符串进行二进制运算时，某execution trace可 以cycles of 32 steps 来实现一个运算。（因32*8=256）
在每一个step，对应为byte-wise操作 和 ‘carries’ 或其它任何辅助值信息，来构成computation trace。
此外，每个256-bit字符串（2个输入、1个输出）使用8个 32-bit的寄存器来表示。

3.2 Main状态机与Binary状态机的连接

Polygon zkEVM的Main状态机的execution trace 与 Binary状态机的execution trace 之间的约束是通过一个Plookup来连接的——即，当cycle结束（即名为RESET的寄存器为1）时，会对Binary状态机execution trace中的每一行进行运算。该Plookup会检查相应的operation code、输入和输出的256-bit字符串的寄存器 以及 最终的carry。

4. Byte-wise运算

由于Polygon zkEVM Binary状态机选用byte plookups，因此接下来将256-bit运算转换为了byte-wise运算。

将$256$-bit整数$\mathbf{a}$表示为：$(a_{31},\dots ,a_1,a_0)$，即：
$$\mathbf{a}=a_{31}\cdot (2^8{)}^{31}+a_{30}\cdot (2^8{)}^{30}+\cdots +a_1\cdot 2^8+a_0=\sum _{i=31}^0{a}_i\cdot (2^8{)}^i,$$
其中每个$a_i$为一个字节，其取值范围为$0$到$2^8-1$。

如$\mathbf{a}=29967$，将其按byte分解表示为$\mathbf{a}=(0x75,0x0F)$，因$\mathbf{a}=29967=以上是关于Polygon\; zkEVM\; Binary状态机的主要内容，如果未能解决你的问题，请参考以下文章$

Polygon zkEVM Memory Align状态机

Polygon zkEVM可验证计算简单状态机示例

Polygon zkEVM Arithmetic状态机

Polygon zkEVM哈希状态机——Keccak-256和Poseidon

Polygon zkEVM的pil-stark Fibonacci状态机代码解析

Polygon zkEVM的pil-stark Fibonacci状态机初体验