机器学习算法：支持向量机 SVM

Posted 2021-04-26 腐烂的橘子

一、简介

支持向量机是机器学习算法中的一个非常强大的分类算法，它的目标不仅是分类数据，还会寻找最佳潜在曲线。

比如下面这两组数据，你要做的是找到一条线，将这两组样本分开。划分的方式有很多，但是你认为哪条线更好地划分了这些点呢？

如果你选择了右边的直线，恭喜你回答正确。直观上来讲，我们应该尽量使这条线位于两个样本的“中间”，这样该划分超平面对训练样本的局部扰动的“容忍性”最好。简单来讲，支持向量机就是这样工作的。

现在你已经有了基本的概念，下面让我们进一步了解一下。

二、误差最小化

首先我们回顾一下什么叫做分类，分类就是找到一条线来划分这些点，如下图中的黄色线所示。而支持向量机的要求则更高一些，即找到一条黄色的线使得白色虚线的间隔尽可能地大。

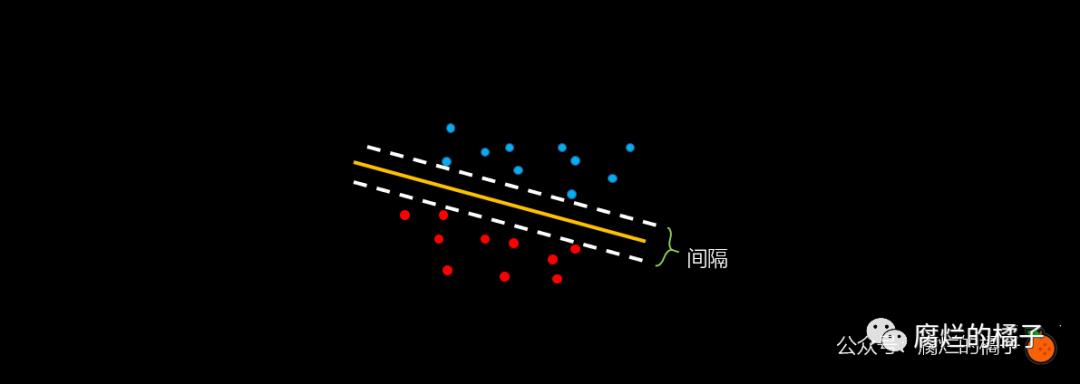
上面的例子比较特殊，我们再来看一个稍微复杂一些的例子：

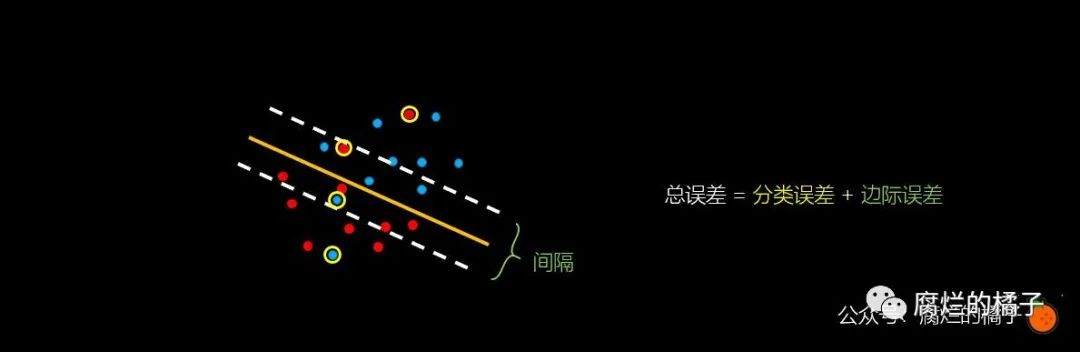
这次我们仍然用黄色的线对样本进行了划分，不同的是，有一些点被错误地进行了分类，即图中用黄色圆圈圈起来的点。

这次我们仍然想要虚线的间隔尽可能地大。通过思考我们发现，我们有两种方式来衡量这个模型。一种是看它错误分类了多少点，另一种是看这两个虚线的间隔到底有多宽。

误分类的点就是用黄色圆圈圈起来的点，我们称之为分类误差；除此之外，我们还希望如之前的图一样，虚线间隔内没有点存在，我们要惩罚这些点，将它作为边际误差。总之，我们得到一个基本的结论：

将此误差最小化，有助于我们学习支持向量机的算法。

三、分类误差

为了构建这个误差函数，我们先来简单回顾一下感知器算法。

假设我们现在有一些点需要我们找到一条完美的直线将他们分开，现在我们有了一条黄色的线 ，其中 和 为向量而 为标量（比如 ）,我们希望使用误差函数来惩罚这些被错误分类的点。

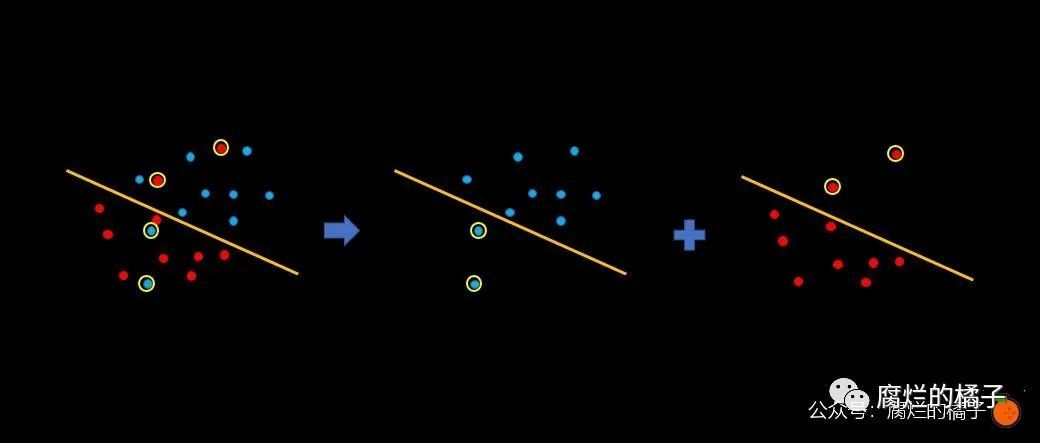
如上图所示，我们将红色和蓝色的点分开，发现黄色圆圈圈起来的点是被错误分类的点。我们惩罚的原则就是：被错误分类的点中，离直线越远的点，受到的惩罚越大；相反，如果离直线越近，受到的惩罚则越小。

下面我们来计算一下这四个点的误差到底是多少。被错误分类点的误差等于该点到直线的距离，其实就是 的值。

图中我们已经将每个值表示的直线标出。通过观察发现，左边两个蓝色点的误差分别为 1 和 3，而右边红色点的误差分别为 1.5 和 3.5，因此总误差就是 。

现在我们知道了这个模型的误差是 9，然后，我们通过梯度下降法来最小化误差，从而找到理想的 和 来获得可能给出的理想分割，这就是感知器算法。

回顾完感知器算法，现在我们只需做一件同样的事，不同的是加入了支持向量机的算法。

这次，我们将惩罚下边界上方的错误分类的红点，和上边界下方错误分类的蓝点。

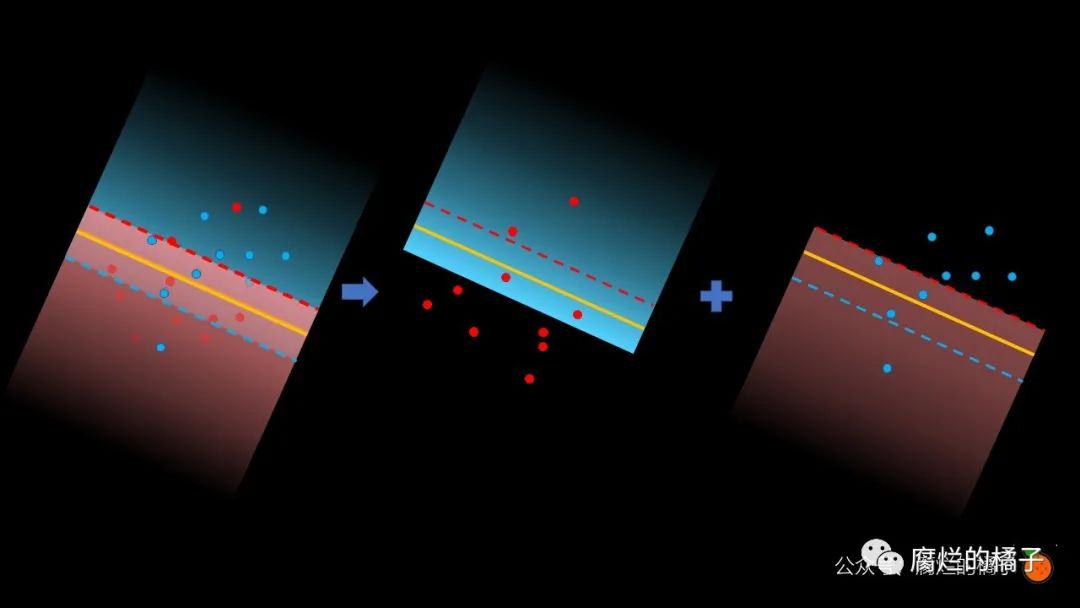
是的，计算这些错误分类点的误差方法和感知器的计算方法完全一样！

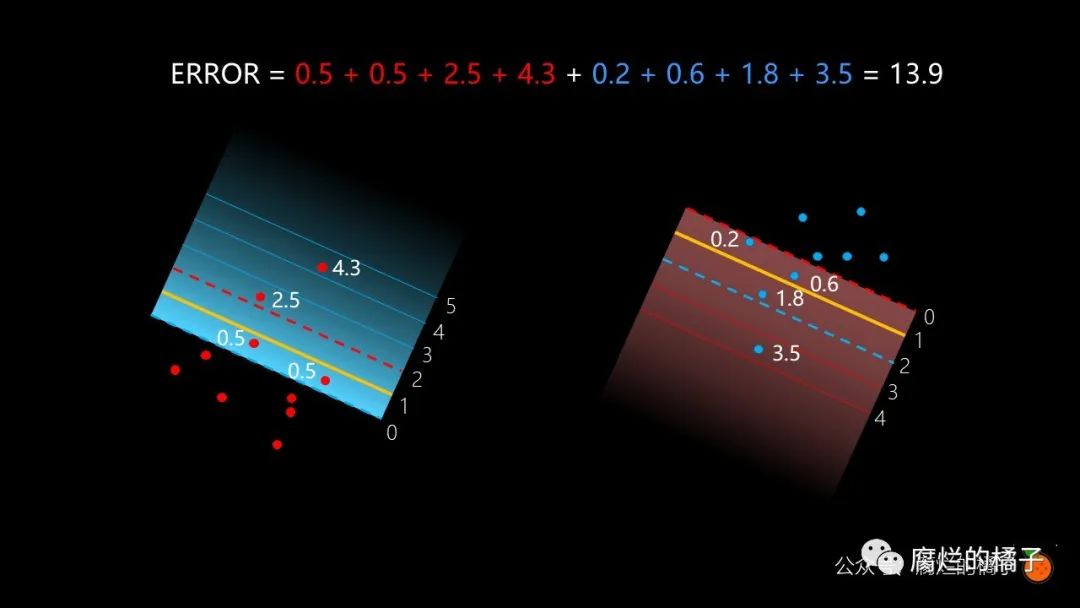
同样地，我们看到蓝色区域有四个错误分类的红点，误差是 ， 红色区域有四个错误分类的点，误差是 ，因此总误差是 。而这个误差，就是支持向量机的误差。

四、边际误差

我们再来讨论一下间隔的问题。间隔就是两条虚线之间的距离，现在我们想要把间隔转化为误差，这样就能使用梯度下降法将误差最小化。我们将编写一个函数，这个函数可以使得间距增大时，误差减小；而在间距减小时，误差增大，如下图所示。

这个函数其实很简单，我们只需将两条曲线的函数选择成 和 ，这时它们之间的间隔就是 ，因为我们想要当间隔增大时误差减小，而我们又不想用绝对值来表示，因此误差可以等于 。这个误差就是边际误差。

这里需要注意一点的是，因为我们之前谈到 是一个向量，因此 。

到这里，我们的支持向量机基本公式已经得到了，即：

意思就是找到一个一个合适的 和 ，使得间隔最大。显然，最大化间隔等价于最小化 。于是上面的式子可以重新改写为

这就是支持向量机（Support Vector Machine，SVM）的基本型，相信你会发现其实并不难。

五、误差函数

我们已经知道了分类误差和边际误差，只需将它们合在一起，就是支持向量机的误差。那我们如何最小化误差呢？只需通过梯度下降法来最小化误差即可。

总结

支持向量机是机器学习算法中很重要的一个算法，而在算法面试中面试官也会经常问到支持向量机的问题。很多情况下，我们是只知其一，不知其二，知道有支持向量机这个模型，谈到公式层面时却无所适从。现在我们知道支持向量机其实就是讲述了一个如何通过改变 和 来使得间距最大而误差最小的故事。了解了基本层面后，我们下次将再来讲讲支持向量机中的核函数问题。

觉得好看，点亮“在看”