机器学习的分类算法之SVM（支持向量机）

Posted 2021-04-26 畅游DT时代

引言

SVM（Support Vector Machine，支持向量机）是机器学习中的有监督线性分类算法，最初正式发表于1995年[Cortes and Vapnik, 1995]。SVM在文本分类尤其是针对二分类任务显示出卓越的性能，因此得到了广泛的研究和应用，后期在多分类任务也进行了专门推广[Hsu and Lin, 2002]。下面从二维线性分类问题出发引入SVM。

SVM：从二维线性分类器出发

以二维空间（平面）中的二分类问题为例，如下图所示：

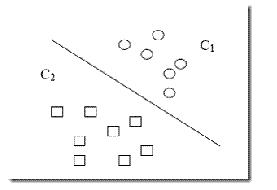
C1和C2是平面上要区分开的两类，中间的那条直线是一个线性函数。通常，如果样本的两类可以用线性函数区分开的，称为数据是线性可分的，否则，称为线性不可分。所谓线性函数，是指拥有一个变量的一阶多项式函数。在二维空间（平面），线性函数呈现为一条直线，而在一维空间（一条直线），线性函数退化为一个点。同理，在三维空间，线性函数是一个平面。不区分维数的情况下，统称这里的线性函数为“超平面”。因此，超平面的表达式为：

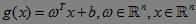
这里，ω、x是n维空间里的实向量；x是函数变量；ω是法向量，决定了超平面的方向；b为位移项；g(x)是实值函数（即函数的值是连续的实数）。对于二维空间，n=2；对于二维空间的线性分类问题，每一个x属于二维空间的样本数据。由于为了方便描述分类，可以取阈值为0，即分类直线描述为: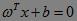。当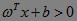时为C1类，当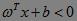时为C2类（当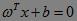时不判断）。此时判别函数为f(x)=sgn[g(x)]注意到，阈值并不是唯一的，旋转或平移上述分类直线可能并不影响分类结果。如何寻找对训练集外的样本分类影响最小的直线呢？通常采用的依据为“分类间隔”。

SVM的基本型

进行文本分类时，将训练样本集表示为：

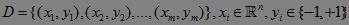
每一个样本点：Di=(xi,yi)。注意，每一个样本点可能维数很高。样本Di=(xi,yi)到超平面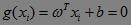的"距离”di计算过程为:

a)     设点xi在超平面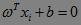的投影为xi撇，则。

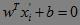b)     注意到向量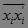和法向量ω平行，因此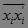和法向量ω的夹角θ为0，有

。

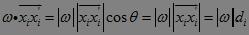这里的符号|ω|是指向量ω的长度，通常指的是它的2-范数。

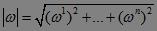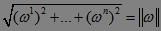，通常记，则：

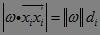
c)      由于

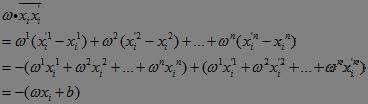
则，

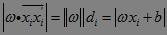
于是有，

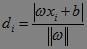
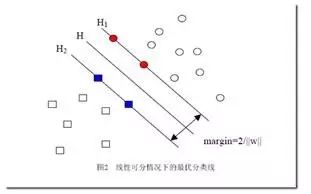
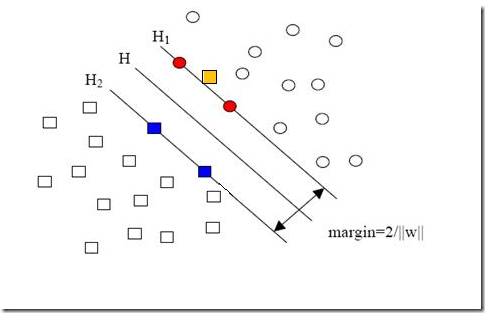
di称为几何间隔，它表示的正是点xi到超平面ωxi+b=0的欧氏距离。某类样本集到超平面的距离我们定义为该样本集合内的样本到超平面的最短距离，因此要求得di的最小值。固定|ωxi+b|，这里当|ωxi+b|=1时，有间隔（margin）为（如下图所示）：

γ=2di=2/||ω||

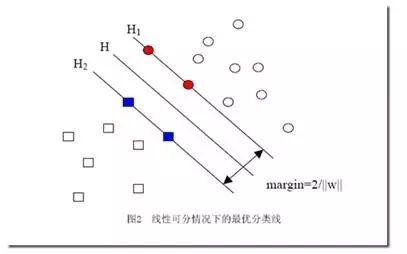
注意到图2中距离超平面最近的蓝色方框样本点和红色圆圈样本点使得等号成立，即ωxi+b=1，以及ωxi+b=-1，因此它们被称为“支持向量”（Support Vector）。要找到具有最大值的“间隔”γ，也就是找到满足如下式子中的ω和b使得γ最大，即：

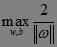
最大化||ω||的倒数等价于最小化||ω||的平方，因此，上式的等价问题为：

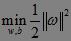
如果不考虑上述优化问题的约束，那么取||ω||=0即为最优解，事实上由于固定分类边界的支持向量为ωxi+b=1,yi=1或ωxi+b=-1,yi=-1，隐含的约束为对于其它非边界点有：

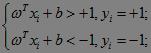
即分类问题的约束为：

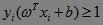
于是，支持向量机SVM的基本型可重新记为：

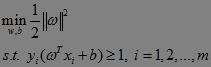
需要注意的是，由于硬性要求所有训练样本点都满足和分类平面间的距离必须大于某个值（不忽略任意一个训练样本），这里的几何间隔称为“硬间隔”。

SVM：线性分类器问题求解的转化——凸二次规划

在继续之前，我们先介绍最优化理论中的凸二次规划。函数f(x)在一组约束下的最小值（或最大值）的优化问题有如下基本形式：

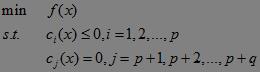
这里，ci(x)<=0,(i=1,2,…,p)为不等式约束条件,cj(x)=0,k=p+1,p+2,…,p+q为等式约束条件，f(x)为目标函数。如果目标函数为变量的二次函数，约束条件为变量的线性函数，可行域（约束条件划分出的空间）为凸集，则称该最优化问题为凸二次规划（凸二次优划）问题。凸二次规划问题的优点在于最优化理论已经证明它有解，且为全局最优解，而且这个解可以找到！求解约束优化问题的重要方法，在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件（广义拉格朗日乘子法），即在满足不等式约束的条件下, 一个非线性规划问题能有最优化解法的一个必要和充分条件。

因此，对于SVM二分类问题：

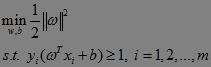
存在一个最优的ω，且可以找到它。即存在一个最优的超平面，使得两类能够区分开。求解的基本思路是，根据最优化理论带有不等式约束的优化问题，将SVM二分类问题转化为它的对偶问题，找出对偶问题中满足KKT条件的解，对偶问题：

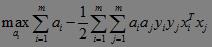
KKT条件：

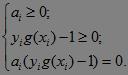
这里的ai是拉格朗日乘子，对于任意训练样本，总有ai=0或者yig(xi)-1=0。再来回顾SVM二分类问题：

要找到n维空间的分类线性函数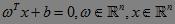，由于样本x是给定、已知的，因此本质就是要确定ω（找到ω，通过等式即可计算出b）。ω是由给定的样本集唯一确定的（全局最优解是唯一的），因此可以表示为：

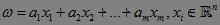
注意到，样本不仅与位置有关，而且与样本的分类符号有关，因此将ω修改为：

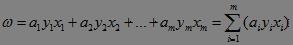
那么，分类线性函数可表示为：

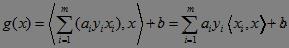
其中ai>=0拉格朗日乘子。由于ai(yig(xi)-1)=0，则对于训练样本，如果ai=0，则该样本不会出现在上述求和的式子中，如果yig(xi)-1=0，则对应的样本点位于间隔边界上，是一个支持向量，因此大部分的训练样本不需要保留，最终的线性函数模型只与支持向量有关。需要注意的是，在通过训练集训练线性分类器时，g(x)中的x是已知的，是给定样本，ω和b才是未知变量。

SVM：核函数

到目前的介绍为止，我们只能解决线性可分的二分类问题，对于非线性可分的问题还没有讨论。例如二维空间中的一个线性不可分问题：

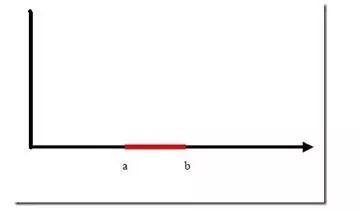
设横轴中红色为正类，黑色为负类，无法找到一个线性函数（一个点）将两类区分开。但是可以找到一个非线性函数将两类区分开，如下图中非线性函数，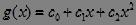

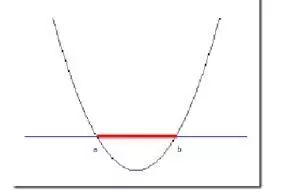
根据目标函数在非线性分类函数的上方或下方可以区分正负两类。虽然g(x)在二维空间不是线性函数，但注意到，当设

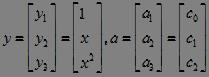
有，

g(x)=g(y)=ay

即在四维空间中解决了二维空间中的线性不可分问题。因此，解决线性不可分问题转化为通过向高维度空间映射，使样本线性可分。那么，选择什么样的高维映射方法才能使得线性不可分的问题能够解决呢？

假设高维空间的线性分类函数为：

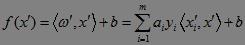
其中， x撇是由x映射而来，ω撇是由常向量ω映射而来，由于我们只关心ω撇和x撇的内积值，而它们又是x和ω的函数，因此我们希望能在低维空间找到一个核函数K，使得

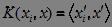
这样我们就不必费力找映射函数了，而这样的K函数也确实存在。Mercer 定理指出，任何半正定的函数都可以作为核函数。此时，所求线性分类器为：

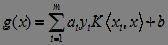
核函数选择是SVM中性能差别的最大原因。核函数选择不合适，意味着样本被映射到了不合适的特征空间，很可能导致性能不佳。虽然核函数的选择没有限制，但现实中通常采用少数几种，常用的核函数有：

高斯核函数是一种经典的径向基核函数（RadialBasis Function 简称RBF），拉普拉斯核是高斯核函数的一个变种，也是一种径向基核函数。

然而在现实中，很难确定合适的核函数使得训练样本在高维空间线性可分，那么，我们关注的问题进一步演变为，如果通过核函数向高维空间映射后，样本仍然是线性不可分的应如何处理？或者虽然找到的核函数使训练集线性可分，但不确定是否是由于过拟合造成的。解决问题的办法就是允许SVM在一些训练样本上出错，将前面所述的“硬间隔”改为下面所述的“软间隔”，即允许部分训练样本不满足约束：

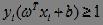
SVM：软间隔

在前述二维线性分类问题的基础上，考虑有一个样本，使得原本线性可分的问题变成了线性不可分，如下图中黄色方框：

引入“松弛变量”>=0来描述两类点间隔比1小的情况，

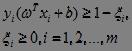
那么优化的目标函数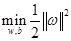由于松弛变量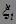的存在而趋于增大，我们用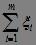来衡量松弛变量对目标函数带来的损失，并用常数C（称为惩罚因子）来表示我们对松弛变量的重视程度，因此常用的“软间隔支持向量机”目标函数表示为，

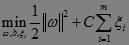
在这个目标函数里，我们注意到，C无穷大时，说明我们不想放弃任意一个训练样本点，此时，只要有一个点离群，目标函数的值马上变成无限大，则问题变成无解，这就退化成了硬间隔问题。C为有限值时，说明我们允许部分训练样本点不满足大于等于1的约束。软间隔SVM仍然是一个二次规划问题，解决方法和硬间隔SVM类似，不再赘述。

一个例子：LibSVM和sklearn.svm

LibSVM是一个开源的SVM软件包，由台湾大学林智仁(Lin Chih-Jen)教授等开发设计，目前提供多种语言版本。LibSVM包含了针对径向基函数和其它核函数的支持，能够对SVM模型进行训练、给出预测，是机器学习中一个经典的工具箱。

Sklearn中的SVM分为SVC（支持向量分类）和SVR（支持向量回归）模块。SKlearn中使用SVC的一个例子（Recognizing hand-written digits）见如下链接：

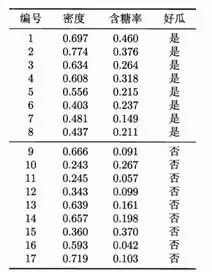
这里，我们使用《机器学习》（周志华）给出的西瓜数据集来测试，西瓜数据集如下：

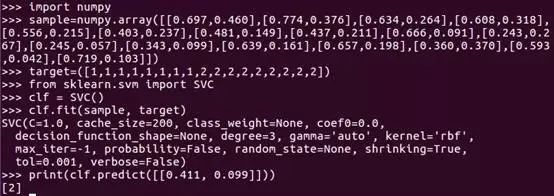
Import numpy

Sample=numpy.array([[0.697,0.460],[0.774,0.376],[0.634,0.264],[0.608,0.318],[0.556,0.215],[0.403,0.237],[0.481,0.149],[0.437,0.211],[0.666,0.091],[0.243,0.267],[0.245,0.057],[0.343,0.099],[0.639,0.161],[0.657,0.198],[0.360,0.370],[0.593,0.042],[0.719,0.103]])

Target=([1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2])

from sklearn.svm import SVC

clf = SVC()

clf.fit(Sample, Target)

print(clf.predict([[0.411,0.099]]))

总结

本文简介了SVM的基本理论，给出了SKlearn一个简短的应用示例。在本文的基础上，可进一步讨论SVM的结构风险、基于支持向量的线性回归以及基于支持向量的多类分类等问题。

-END-

声明：

本文为中国联通网研院网优网管部IT技术研究团队独家提供。

如需转载或合作，请联系管理员（[e-mail]）

---

长按既可添加关注

---