auc原理与实现

Posted 2023-05-16

参考技术A

AUC（Area under curve）是机器学习常用的二分类评测手段。
AUC：一个正例，一个负例，预测为正的概率值比预测为负的概率值还要大的可能性。
所以根据定义：我们最直观的有两种计算AUC的方法

ROC曲线指受试者工作特征曲线 / 接收器操作特性曲线(receiver operating characteristic curve), 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系，它通过将连续变量设定出多个不同的临界值，从而计算出一系列敏感性和特异性，再以敏感性为纵坐标、（1-特异性）为横坐标绘制成曲线，曲线下面积越大，诊断准确性越高。

auc直接含义是ROC曲线下的面积，如下图：

AUC直观地反映了ROC曲线表达的分类能力。

假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0),阈值最小时，对应坐标点(1,1)。

一个通俗解释：

降序rank--> 去掉（正，正）样本对数--> 求取比例

其实就是，按正样本score降序排列情况下，负样本pk失败的数目总数占所有样本对的比例。 （网上说取M，M-1，……1比M-1，M-2，……1更简便的，个人以为理解错了，其实不是去掉了比rank_i的score低的i-1个（正，正）样本对，而是留下了失败的（正，负）样本对）

知乎的解释： https://www.zhihu.com/question/39840928

参考：
https://blog.csdn.net/natsuka/article/details/78546645
https://blog.csdn.net/u013385925/article/details/80385873
https://zhuanlan.zhihu.com/p/35583721
https://blog.csdn.net/hnu2012/article/details/87892368

练习1 循环拟合与AUC

logistic回归、SVM、AUC、ROC

R需要包：mice包；AUC包或pROC包

需要知识:logistic回归；SVM；GAM；缺失值多重插补法；拟合效果ROC、AUC

 

In cancer studies, a question of critical interest is the progression of cancer. Here we consider a study on cancer progression.

The dataset contains the following variables:

Response: cancer development, which is a binary variable indicating whether there is any new cancer development;

Covariates: we have six covariates: size, stage, age, treatment type, dose I, dose II. Among them, stage and treatment type are categorical; the reminders are continuous.

Our question: in clinical practice, whether it is possible to predict cancer development using the six covariates we measure.

数据示例如下

 

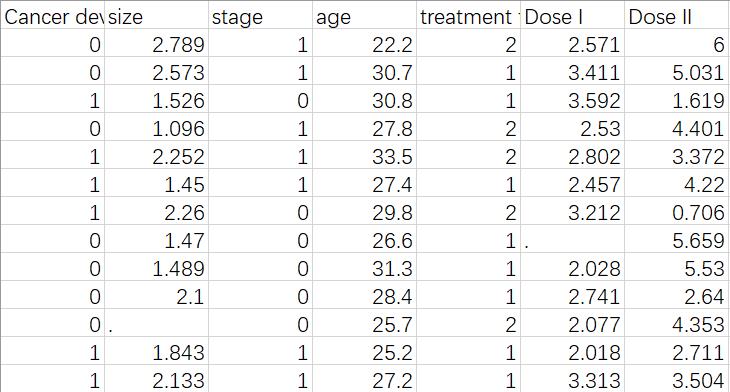
Cancer development: Yes (coded as 1) or No (coded as 0)

size: tumor size (which is measured with the diameter of tumor)

stage: tumor stage (categorial)

age: age (continuous)

treatment type: different type of treatment

Dose I: dose of drug A

Dose II: dose of drug B

".": missing measurements. You can assume MAR.

 

• 读取数据

cancer <- read.csv("cancer-pred.csv", stringsAsFactors = FALSE)
cancer <- cancer[ , 1:7]
str(cancer)

查看数据结构，200个观测值和7个变量，并且存在缺失值。

由于数据集中缺失值由点号代替，故读取后变量为字符型，需将其转化为数值型。

无法通过设置read.csv中参数na.strings="."实现跳过转化步骤，因为最后两个变量含有小数点。

cancer <- sapply(cancer, as.numeric)     #警告信息是由于点号转化为NA值
cancer <- as.data.frame(cancer)          #转化为数据框更适用于建模
colnames(cancer) <- c("develop", "size", "stage", "age", "type",  "Dose.I", "Dose.II")

• 探索性分析

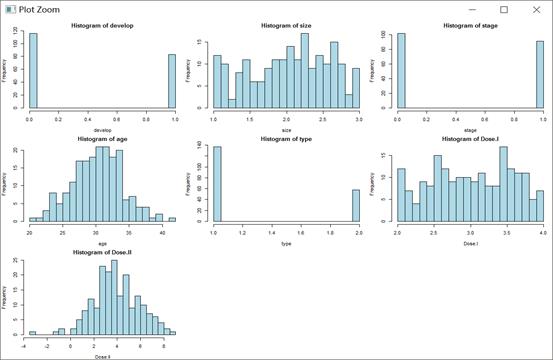
变量箱线图、柱状图、连续变量相关图，图片仅展示柱状图

old.par <- par(mfrow=c(3, 3))
apply(cancer, 2, boxplot)             
par(old.par)

par(mfrow=c(3, 3), mar=c(4, 4, 2, 0.5))
for (j in 1:ncol(cancer)) {
  hist(cancer[ , j], xlab=colnames(cancer)[j],
       main=paste("Histogram of", colnames(cancer)[j]),
       col="lightblue", breaks=20)
}
par(mfrow=c(1, 1))

pairs(~size+age+Dose.I+Dose.II, data=cancer)

•  补全缺失值

对于缺失值的处理方法有几种，参考《R语言实战》

此处处理方法有三种：删除缺失值，平均值众数替代法，多重插补法。

# #缺失值删除法
# cancer <- na.omit(cancer)
# #平均数众数替代法
# cancer.mean <- sapply(cancer[c(2, 4, 6, 7)], mean, na.rm=TRUE)
# cancer.table <- sapply(cancer[ , c(1, 3, 5)], table)
# cancer[which(is.na(cancer[ , 2])), 2] <- round(cancer.mean[1], 3)
# cancer[which(is.na(cancer[ , 4])), 4] <- round(cancer.mean[2], 1)
# cancer[which(is.na(cancer[ , 6])), 6] <- round(cancer.mean[3], 3)
# cancer[which(is.na(cancer[ , 7])), 7] <- round(cancer.mean[4], 3)
# for(i in c(1, 3, 5)){
#   cancer[which(is.na(cancer[ , i])), i] <- 
#     as.numeric(rownames(cancer.table)[which.max(cancer.table[1])])
# }
# #多重插补法
imp <- mice(cancer, seed=1)
fit <- with(imp,glm(develop~., family=binomial, data = cancer))
pooled <- pool(fit)
cancer <- complete(imp,action=3)

cancer[ , c(3, 5)] <- sapply(cancer[ , c(3, 5)], as.factor)   #部分变量转化为因子

• 抽样拟合计算AUC

1. logistic回归

将数据分为训练集（150个样本）和测试集（50个样本），用训练集拟合logistic模型，用得到的模型对测试集的因变量进行预测

将预测值与真实值比较得到错判矩阵、tpr、fpr，针对不同的cutoffs得到roc曲线并计算AUC值。

将以上步骤循环3000次处理，对3000个AUC取平均并进行t检验。

cancer.auc <- c(length=3000)    #生成空向量以填充
for (i in 1:3000){
  set.seed(i)
  sample.i <- sample(1:nrow(cancer), 3/4*nrow(cancer))
  cancer1  <- cancer[sample.i, ]; cancer2 <- cancer[-sample.i, ]
  glm.can  <- glm(develop~., data=cancer1)
# glm.new  <- step(glm.can, trace=0)   #trace=0不返回结果
  cancer.pred   <- predict(glm.can, family=binomial, 
                           newdata = cancer2, type = "response")
  cancer.roc    <- roc(cancer.pred, as.factor(cancer2$develop))
  cancer.auc[i] <- auc(cancer.roc)
}

mean(cancer.auc)            #3000次AUC均值
t.test(cancer.auc, alternative = "greater", mu=0.5)

hist(cancer.auc, freq = F, breaks = 40) 
lines(density(cancer.auc, bw=0.05), col="red", lwd=2)

　　

 

 

因变量为是否型，虽然t检验通过，但是预测效果并不好

 

2. 支持向量机（SVM）

下面使用支持向量机的方法

#SVM
cancer.auc <- c(length=3000)
for (i in 1:3000){
  set.seed(i)
  sample.i <- sample(1:nrow(cancer), 3/4*nrow(cancer))
  cancer1  <- cancer[sample.i, ]; cancer2 <- cancer[-sample.i, ]
  cancer.svm <- svm(develop~., data=cancer1kernel= "linear")
  cancer.pred   <- predict(cancer.svm, newdata = cancer2, 
                           type="response")
  cancer.roc    <- roc(cancer.pred, as.factor(cancer2$develop))
  cancer.auc[i] <- auc(cancer.roc)
}
mean(cancer.auc)
t.test(cancer.auc, alternative = "greater", mu=0.5)

尝试SVM四种核方法，即kernel参数“linear”、“polynomial”、“radial”、“sigmoid”

最后线性方法得到AUC均值最大，但也只有0.5837262，与logistic模型相比并不具有显著优势

 

3. 广义加性模型（GAM）

#GAM
cancer.auc <- c(length=300)
for (i in 1:300){
  set.seed(10*i)
  # set.seed(3)
  sample.i <- sample(1:nrow(cancer), 3/4*nrow(cancer))
  cancer1  <- cancer[sample.i, ]; cancer2 <- cancer[-sample.i, ]
  cancer.gam <- gam(develop ~ s(size, bs="cr") + stage + 
                      s(age, bs="cr") + type + s(Dose.I, bs="cr") +
                      s(Dose.II, bs="cr"), family = binomial, 
                    data=cancer1, trace=TRUE)
  cancer.pred   <- predict(cancer.gam, newdata = cancer2, 
                           type="response")
  cancer.roc    <- roc(cancer.pred, as.factor(cancer2$develop))
  # auc(cancer.roc)
  cancer.auc[i] <- auc(cancer.roc)
}
mean(cancer.auc)
t.test(cancer.auc, alternative = "greater", mu=0.5)

　　GAM函数得到300次AUC均值为0.5694343，且GAM循环3000次较GLM运算速度相比很慢

 

 

Tips:

问题一：随机抽样，以下得到的试验集与测试集不是互补关系，会导致AUC上升。

   set.seed(1)

   cancer1  <-  cancer[sample(1:nrow(cancer),  3/4*nrow(cancer)),  ]

   cancer2  <-  cancer[-sample(1:nrow(cancer),  3/4*nrow(cancer)),  ]

问题二：三种处理缺失值方法（缺失值剔除法、均值众数替代法、多重插补法）结果相差不大，差距在0.01左右。

问题三：DoseII数据出现小于0的值如果当作异常值处理删去结果为0.5770816，不处理结果为0.5873808，AUC降低了0.01，故放弃。

问题四：循环中使用step函数筛选不显著变量，AUC降低0.3左右，故放弃。

问题五：计算AUC值有两个包“AUC”和“pROC”，两个包roc函数参数输入方式不同。设立了随机数种子，但是二者得到结果测试集差0.01，试验集到小数点后20位才不一致，未确定是用AUC计算方式不同解释还是测试集出现问题解释。

 

若需原始数据试验可回复联系