机器学习：基于sklearn的AUC的计算原理

Posted 2020-11-24 xiaofeiido

AUC原理

一、AUC起源

AUC是一种用来度量分类模型好坏的一个标准。这样的标准其实有很多，例如：大约10年前在 machine learning文献中一统天下的标准：分类精度；在信息检索(IR)领域中常用的recall和precision，等等。其实，度量反应了人们对” 好”的分类结果的追求，同一时期的不同的度量反映了人们对什么是”好”这个最根本问题的不同认识，而不同时期流行的度量则反映了人们认识事物的深度的变 化。近年来，随着machine learning的相关技术从实验室走向实际应用，一些实际的问题对度量标准提出了新的需求。特别的，现实中样本在不同类别上的不均衡分布(class distribution imbalance problem)。使得accuracy这样的传统的度量标准不能恰当的反应分类器的performance。

举个例子：测试样本中有A类样本90个，B 类样本10个。分类器C1把所有的测试样本都分成了A类，分类器C2把A类的90个样本分对了70个，B类的10个样本分对了5个。则C1的分类精度为 90%，C2的分类精度为75%。但是，显然C2更有用些。

另外，在一些分类问题中犯不同的错误代价是不同的(cost sensitive learning)。这样，默认0.5为分类阈值的传统做法也显得不恰当了。 

为了解决上述问题，人们从医疗分析领域引入了一种新的分类模型performance评判方法——ROC分析。

ROC分析本身就是一个很丰富的内容，有兴趣的读者可以自行Google。

二、ROC曲线

 

roc曲线：接收者操作特征(receiveroperating characteristic),roc曲线上每个点反映着对同一信号刺激的感受性。

横轴：负正类率(false postive rate FPR)特异度，划分实例中所有负例占所有负例的比例；(1-Specificity)

纵轴：真正类率(true postive rate TPR)灵敏度，Sensitivity(正类覆盖率)

2针对一个二分类问题，将实例分成正类(postive)或者负类(negative)。但是实际中分类时，会出现四种情况.

(1)若一个实例是正类并且被预测为正类，即为真正类(True Postive TP)

(2)若一个实例是正类，但是被预测成为负类，即为假负类(False Negative FN)

(3)若一个实例是负类，但是被预测成为正类，即为假正类(False Postive FP)

(4)若一个实例是负类，但是被预测成为负类，即为真负类(True Negative TN)

TP:正确的肯定数目

FN:漏报，没有找到正确匹配的数目

FP:误报，没有的匹配不正确

TN:正确拒绝的非匹配数目

列联表如下：

 

 

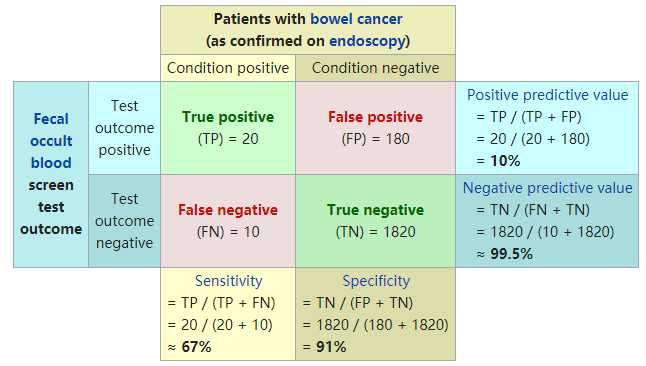
由上表可得出横，纵轴的计算公式：

(1)真正类率(True Postive Rate)TPR: TP/(TP+FN),代表分类器预测的正类中实际正实例占所有正实例的比例。Sensitivity

(2)负正类率(False Postive Rate)FPR: FP/(FP+TN)，代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity

(3)真负类率(True Negative Rate)TNR: TN/(FP+TN),代表分类器预测的负类中实际负实例占所有负实例的比例，TNR=1-FPR。Specificity

假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0),阈值最小时，对应坐标点(1,1)。

如下图中实线为ROC曲线，线上每个点对应一个阈值。

 

 

 

 

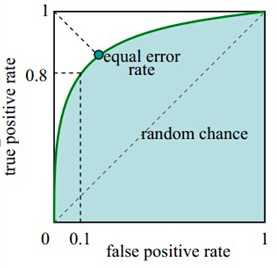
横轴FPR:1-TNR,1-Specificity，FPR越大，预测正类中实际负类越多。

纵轴TPR：Sensitivity(正类覆盖率),TPR越大，预测正类中实际正类越多。

理想目标：TPR=1，FPR=0,即图中(0,1)点，故ROC曲线越靠拢(0,1)点，越偏离45度对角线越好，Sensitivity、Specificity越大效果越好。

三、绘制ROC曲线

假设已经得出一系列样本被划分为正类的概率，然后按照大小排序，下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率。

 

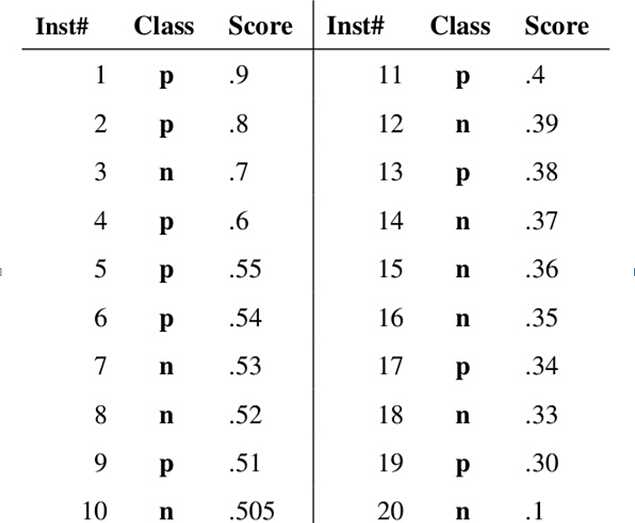
接下来，我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本（预测标签），否则为负样本（预测标签）。

举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本（预测标签），因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本（预测标签）。每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：

 

 

 

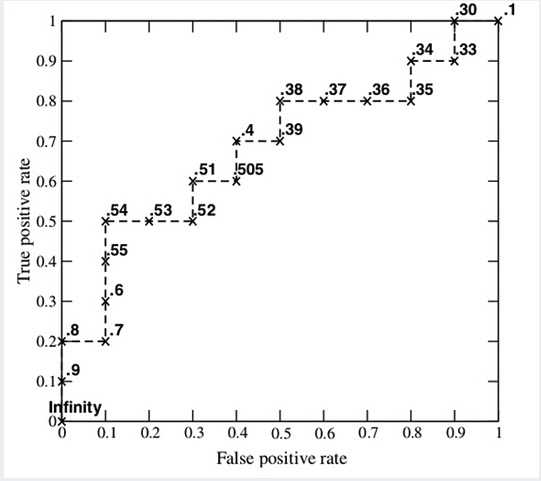
AUC(Area under Curve)：Roc曲线下的面积，介于0.1和1之间。Auc作为数值可以直观的评价分类器的好坏，值越大越好。

首先AUC值是一个概率值，当你随机挑选一个正样本以及负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好地分类。

接下来，我们来具体一个实现的列子：

sklearn给出了一个计算roc的例子：

y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)

通过计算，得到的结果（TPR, FPR, 截断点）为

fpr = array([ 0. ,  0.5,  0.5,  1. ])
tpr = array([ 0.5,  0.5,  1. ,  1. ])
thresholds = array([ 0.8 ,  0.4 ,  0.35,  0.1 ])    #截断点

详细计算过程：

y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])

 (1). 分析数据

y是一个一维数组（样本的真实分类）。数组值表示类别（一共有两类，1和2）。我们假设y中的1表示反例，2表示正例。即将y重写为：

y_true = [0, 0, 1, 1]

score即各个样本属于正例的概率。

(2). 针对score，将数据排序

样本	预测属于P的概率(score)	真实类别
y[0]	0.1	N
y[2]	0.35	P
y[1]	0.4	N
y[3]	0.8	P

(3). 将截断点依次取值为score值

将截断点依次取值为0.1, 0.35, 0.4, 0.8时，计算TPR和FPR的结果。

 3.1. 截断点为.01

说明只要score>=0.1，它的预测类别就是正例。 
此时，因为4个样本的score都大于等于0.1，所以，所有样本的预测类别都为P。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [1, 1, 1, 1]

 

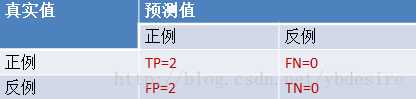
TPR = TP/(TP+FN) = 1 

FPR = FP/(TN+FP) = 1

3.2. 截断点为0.35

说明只要score>=0.35，它的预测类别就是P。 
此时，因为4个样本的score有3个大于等于0.35。所以，所有样本的预测类有3个为P（2个预测正确，1一个预测错误）；1个样本被预测为N（预测正确）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 1, 1, 1]

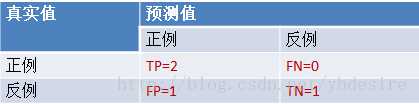
TPR = TP/(TP+FN) = 1 
FPR = FP/(TN+FP) = 0.5

3.3. 截断点为0.4

说明只要score>=0.4，它的预测类别就是P。 
此时，因为4个样本的score有2个大于等于0.4。所以，所有样本的预测类有2个为P（1个预测正确，1一个预测错误）；2个样本被预测为N（1个预测正确，1一个预测错误）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 1, 0, 1]

 TPR = TP/(TP+FN) = 0.5 

FPR = FP/(TN+FP) = 0.5

 3.4. 截断点为0.8

说明只要score>=0.8，它的预测类别就是P。所以，所有样本的预测类有1个为P（1个预测正确）；3个样本被预测为N（2个预测正确，1一个预测错误）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 0, 0, 1]

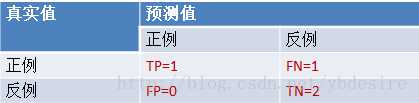
TPR = TP/(TP+FN) = 0.5 
FPR = FP/(TN+FP) = 0

计算完毕！

四、AUC的计算

   1.  最直观的，根据AUC这个名称，我们知道，计算出ROC曲线下面的面积，就是AUC的值。事实上，这也是在早期 Machine Learning文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此，计算的AUC也就是这些阶梯 下面的面积之和。这样，我们先把score排序(假设score越大，此样本属于正类的概率越大)，然后一边扫描就可以得到我们想要的AUC。但是，这么做有个缺点，就是当多个测试样本的score相等的时候，我们调整一下阈值，得到的不是曲线一个阶梯往上或者往右的延展，而是斜着向上形成一个梯形。此时，我们就需要计算这个梯形的面积。由此，我们可以看到，用这种方法计算AUC实际上是比较麻烦的。 

   2. 一个关于AUC的很有趣的性质是，它和Wilcoxon-Mann-Witney Test是等价的。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score（在实际预测过程中，分类器总是分别给正负样本一个概率（score）值，并根据设定的阈值，将样本预测为正或负样本标签）。有了这个定义，我们就得到了另外一中计算AUC的办法：得到这个概率。我们知道，在有限样本中我们常用的得到概率的办法就是通过频率来估计之。这种估计随着样本规模的扩大而逐渐逼近真实值。这和上面的方法中，样本数越多，计算的AUC越准确类似，也和计算积分的时候，小区间划分的越细，计算的越准确是同样的道理。具体来说就是统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。n为样本数（即n=M+N） 
   3.  第三种方法实际上和上述第二种方法是一样的，但是复杂度减小了。它也是首先对score（预测为正标签的概率值或得分）从大到小排序，然后令最大score对应的sample的rank为n=M+N，第二大score对应sample的rank为n-1，以此类推。然后把所有的正类样本的rank相加，再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以M×N。即 

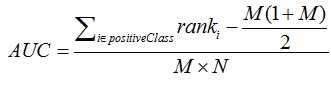
特别需要注意的是，再存在score相等的情况时，对相等score的样本，需要 赋予相同的rank(无论这个相等的score是出现在同类样本还是不同类的样本之间，都需要这样处理)。具体操作就是再把所有这些score相等的样本 的rank取平均。然后再使用上述公式。 

 

 

 

参考：

https://www.cnblogs.com/keye/p/9367347.html

http://www.360doc.com/content/19/0420/21/34772704_830203547.shtml

https://blog.csdn.net/pzy20062141/article/details/48711355