1.6 分类模型的评估方法

Posted 2021-09-07 炫云云

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了1.6 分类模型的评估方法相关的知识，希望对你有一定的参考价值。

分类模型的评估方法

混淆矩阵

在讲矩阵之前，我们先复习下之前在讲分类评估指标中定义的一些符号含义，如下：

正例

如果是预测疾病，这项的结果是“患有疾病”
二元目标变量中的1

负例

如果是预测疾病，这项的结果是“未患有疾病”
二元目标变量中的0

TP(True Positive)真正：将正类预测为正类数，真实为1，预测也为1.
TN(True Negative)真负：将负类预测为负类数，真实为0，预测也为0
FN(False Negative)假负：将正类预测为负类数，真实为1，预测为0
FP(False Positive)假正：将负类预测为正类数，真实为0，预测为1

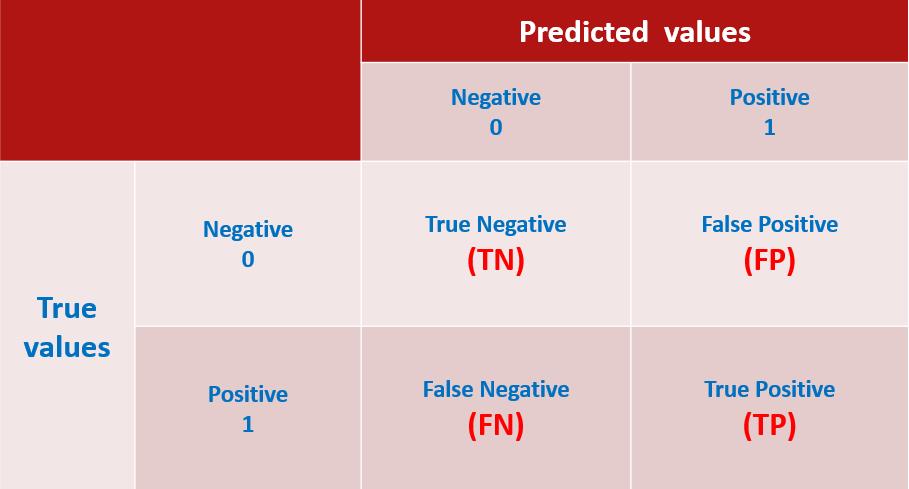
1、混淆矩阵定义及表示含义

混淆矩阵是机器学习中总结分类模型预测结果的情形分析表，以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。

Confusion Matrix，前面的True和False代表预测本身的结果是正确还是不正确的，而后面的Positive和Negative则是代表预测的方向是正向还是负向的。

下面我们先以二分类为例，看下矩阵表现形式，如下：

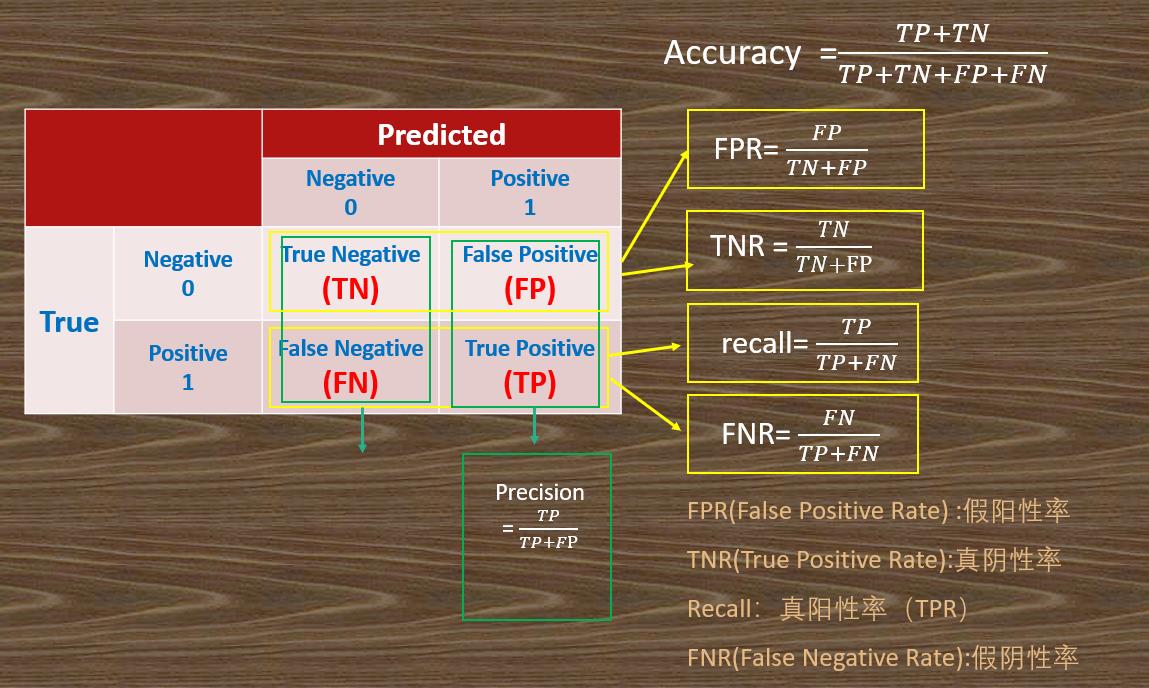
2、评价指标

1）正确率（accuracy）

正确率是我们最常见的评价指标，，这个很容易理解，就是被分对的样本数除以所有的样本数，通常来说，正确率越高，分类器越好；

2）错误率（error rate)

错误率则与正确率相反，描述被分类器错分的比例， $e r r o r r a t e = (F P + F N) / (T P + T N + F P + F N)$ ，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 - error rate；

3）召回率（recall）；灵敏度（sensitivity）也叫真阳性率（TPR） ；

$R e c a l l = T P / (T P + F N)$ ，表示的是正确识别的正例个数在实际为正例的样本数中的占比，衡量了分类器对正例的识别能力；也叫"正例覆盖率"：表示正确预测的正例数在实际正例数中的比例。召回率是覆盖面的度量，该指标反映的是模型能够在多大程度上覆盖所关心的类别。

4）特异度（specificity)，真阴性率(TNR)

$s p e c i f i c i t y = T N / （ T N + F P ）$ ，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力；也叫"负例覆盖率"：正确预测的负例数在实际负例数中的比例。

5）精度（precision），精确率

精度是精确性的度量，表示在预测正例数中，正确预测的比例，即 $p r e c i s i o n = T P / （ T P + F P ）$ ；也叫“正例命中率”。

这个指标在做市场营销的时候非常有用，例如对预测的目标人群做活动，实际响应的人数越多，说明模型越能够刻画出关心的类别。

6）F-Measure(F度量)

计算公式为 :
$F_{\\beta}=\\frac{\\left(\\beta^{2}+1\\right) P R}{\\beta^{2} P+R}$
其中 $\\beta$ 是参数， P是精确率(Precision), R是召回率(Recall)。 $\\beta=1$ 就是F1分数。

7）F1分数(F1-Measure)
$F1\\text{-}score = \\frac{2\\times \\text{Precision} \\times \\text{Recall}}{ \\text{Precision}+\\text{Recall}}$

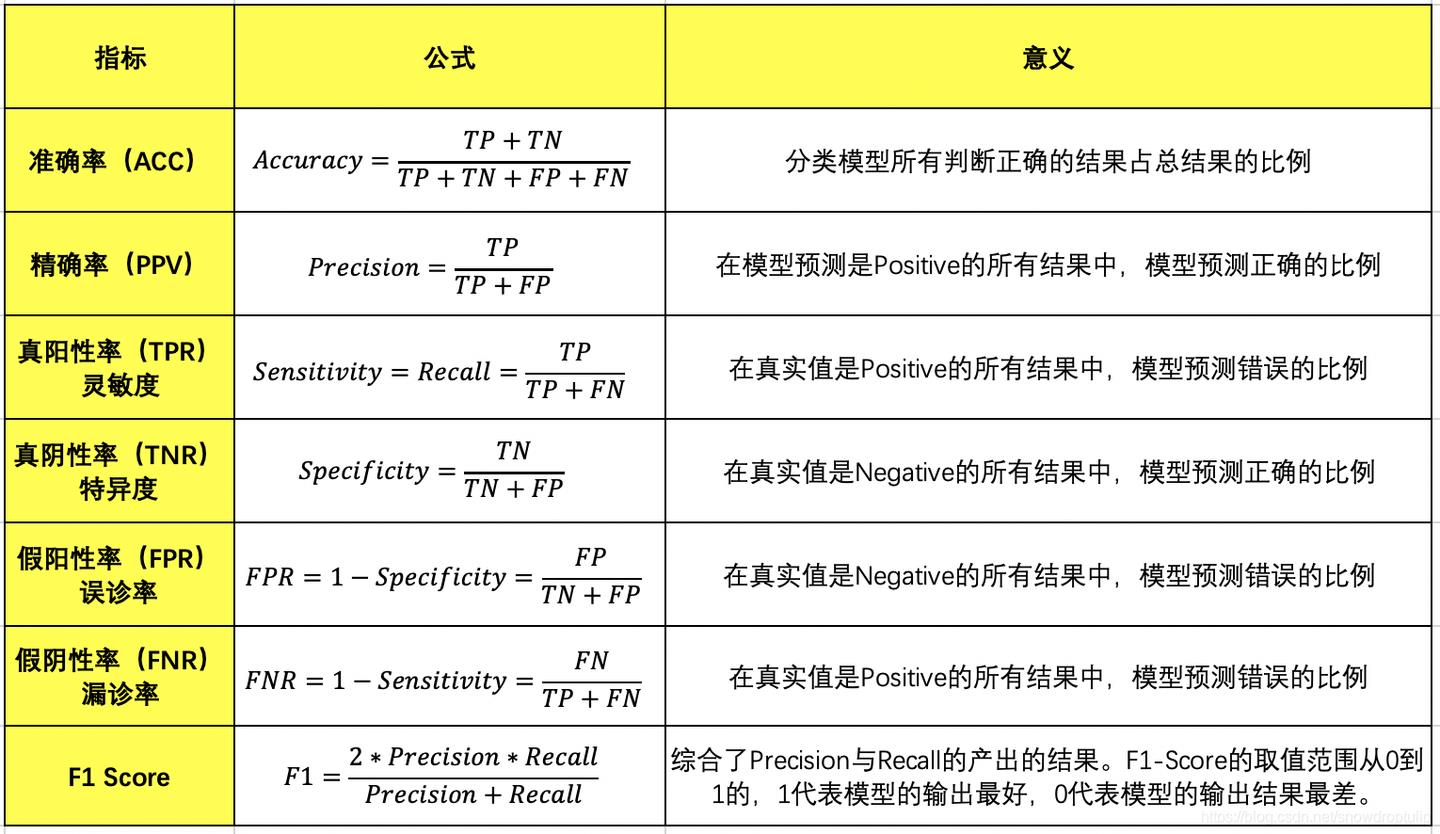
8）其他评价指标

计算速度：分类器训练和预测需要的时间；
鲁棒性：处理缺失值和异常值的能力；
可扩展性：处理大数据集的能力；
可解释性：分类器的预测标准的可理解性，像决策树产生的规则就是很容易理解的，而神经网络的一堆参数就不好理解，我们只好把它看成一个黑盒子。

对于一个给定类，精度和召回率的不同组合如下：

高精度+高召回率：模型能够很好地检测该类；
高精度+低召回率：模型不能很好地检测该类，但是在它检测到这个类时，判断结果是高度可信的；
低精度+高召回率：模型能够很好地检测该类，但检测结果中也包含其他类的点；
低精度+低召回率：模型不能很好地检测该类。

我们举个例子，如下图所示，我们有 10000 个产品的混淆矩阵：

注意「not defective」精度不可计算。

根据上图，准确率为 96.2%，无缺陷类的精度为 96.2%，有缺陷类的精度不可计算；无缺陷类的召回率为 1.0（这很好，所有无缺陷的产品都会被检测出来），有缺陷类的召回率是 0（这很糟糕，没有检测到有缺陷的产品）。因此我们可以得出结论，这个模型对有缺陷类是不友好的。有缺陷产品的 F1 分数不可计算，无缺陷产品的 F1 分数是 0.981。在这个例子中，如果我们查看了混淆矩阵，就会重新考虑我们的模型或目标，也就不会有前面的那种无用模型了。

总结：

3、python实现

我们利用 sklearn中的 confusion_matrix 函数来得到混淆矩阵，函数原型为：

sklearn.metrics.confusion_matrix(y_true , y_pred,labels=None, sample_weight=None)

y_true：样本真实的分类标签列表
y_pred：样本预测的分类结果列表
labels：类别列表，可用于对类别重新排序或选择类别子集。如果默认，则将y_true 或y_pred 中至少出现一次的类别按排序顺序构成混淆矩阵。
sample_weight：样本权重

二分类

from sklearn.metrics import confusion_matrix, classification_report
y_true = [0, 1, 0, 1]
y_pred = [1, 1, 1, 0]
confusion_matrix(y_true,y_pred)

array([[0, 2],
       [1, 1]], dtype=int64)

返回值是一个形状为[n_classes, n_classes]的混淆矩阵，对于二分类模型，这个2x2的矩阵表示如下：

TN|FP
FN|TP

所以我们可以通过ravel()来直接得到这四个值：

tn, fp, fn, tp = confusion_matrix(y_pred, y_true).ravel()

混淆矩阵:

C2= confusion_matrix(y_true,y_pred)#混淆矩阵
sns.heatmap(C2, annot = True, cmap = 'GnBu', fmt = 'd') #画热力图
plt.title('confusion matrix') #标题
#  x轴和y轴标签
plt.xlabel('predicted value ')
plt.ylabel('True value')
# 显示图形
plt.show()

模型的评估报告：

print(classification_report(y_true,y_pred))

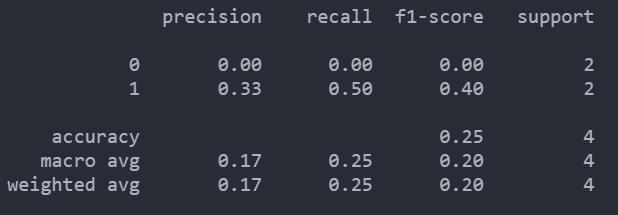
多分类

# classes表示不同类别的名称，比如这有6个类别
classes = ['A', 'B', 'C', 'D', 'E', 'F']

random_numbers = np.random.randint(6, size=50)  # 6个类别，随机生成50个样本
y_true = random_numbers.copy()  # 样本实际标签
random_numbers[:10] = np.random.randint(6, size=10)  # 将前10个样本的值进行随机更改
y_pred = random_numbers  # 样本预测标签

# 获取混淆矩阵
cm = confusion_matrix(y_true,y_pred)#混淆矩阵


sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd') #画热力图
plt.title('confusion matrix') #标题
#  x轴和y轴标签
plt.xlabel('predicted value ')
plt.ylabel('True value')
#设置标签
xlocations = np.array(range(len(classes)))+ 0.5
plt.xticks(xlocations, classes, rotation=90)
plt.yticks(xlocations, classes)
# 显示图形
plt.show()

我们看类别A，预测结果和实际标签都为A的有9个样本，把A样本预测为其他类别的有3个样本（同一行的其他样本），而把其他类别预测为A样本的有0个样本（同一列的其他样本）。其他类别也同样这样分析。

通常我们会在绘图前对混淆矩阵按行做一个标准化处理，即得到的是概率值，每行所有的概率之和为1，所以对角线就代表每个类别的查全率（召回率）。

# Normalize by row
cm_normalized = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print(cm_normalized)

[[0.75       0.08333333 0.         0.08333333 0.         0.08333333]
 [0.         0.77777778 0.         0.11111111 0.11111111 0.        ]
 [0.         0.         1.         0.         0.         0.        ]
 [0.         0.         0.         1.         0.         0.        ]
 [0.         0.         0.         0.         0.88888889 0.11111111]
 [0.         0.         0.11111111 0.         0.         0.88888889]]

模型的评估报告：

print(classification_report(y_true,y_pred))

G-mean

在样本不均衡的情况下，由于少量样本占比较小, 如果仅考虑Error Rate或者 accuracy, 即使模型全部把少量样本分错, 其整体的Error Rate和Accuracy还是比较高的。因此, 对于样本不平衡的情况下，引入另外一个评价指标- $G$ -mean。
$n=\\sqrt{\\frac{T P}{T P+F N} \\times \\frac{T N}{T N+F P}}$

MacroP, MicroP

Precision和Recall只是在一个简单的二分分类的情况下进行评价。当基于同一数据集多次训练/测试不同模型，或者基于多个数据集测试评价同一个模型，再或者执行多分类的任务时，会产生很多混淆矩阵。怎么评价？

macro-P宏查准率和macro-R宏查全率以及macro-F1:
$\\begin{gathered} \\operatorname{marcoP}=\\frac{1}{n} \\sum_{1}^{n} P_{i} \\\\ \\operatorname{marco} R=\\frac{1}{n} \\sum_{1}^{n} R_{i} \\\\ \\operatorname{marcoF} 1=\\frac{2 \\times \\operatorname{macroP} \\times \\operatorname{macro} R}{\\operatorname{macroP}+\\text { macro } R} \\end{gathered}$
micro-P微查准率和micro-P微查全率以及micro-F1: