图的存储结构：必须掌握的深度优先算法和广度优先算法

Posted 2021-04-11 全球人工智能

1.写在前面

图的存储结构有两种：一种是基于二维数组的邻接矩阵表示法。另一种是基于链表的的邻接表。

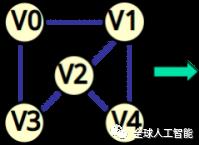
在邻接矩阵中，可以如下表示顶点和边连接关系：

　　　　

说明：

将顶点对应为下标，根据横纵坐标将矩阵中的某一位置值设为1，表示两个顶点向联接。

图示表示的是无向图的邻接矩阵，从中我们可以发现它们的分布关于斜对角线对称。

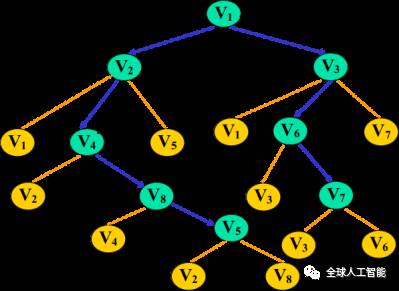
我们在下面将要讨论的是下图的两种遍历方法（基于矩阵的）：

 　　　　

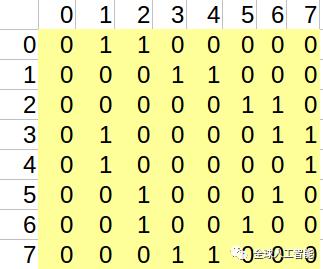
我们已经说明了我们要用到的是邻接矩阵表示法，那么我首先要来构造图：

矩阵图的数据结构如下表示：

这样我们可以首先来创建上述图，为了方便，我们直接在代码中书写矩阵，而不用每次调试手动输入了

这样我们就已经完成了准备工作，我们可以正式来学习我们的两种便利方式了。

2.深度优先遍历算法

分析深度优先遍历

从图的某个顶点出发，访问图中的所有顶点，且使每个顶点仅被访问一次。这一过程叫做图的遍历。

深度优先搜索的思想：

①访问顶点v；
②依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
③若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

比如：

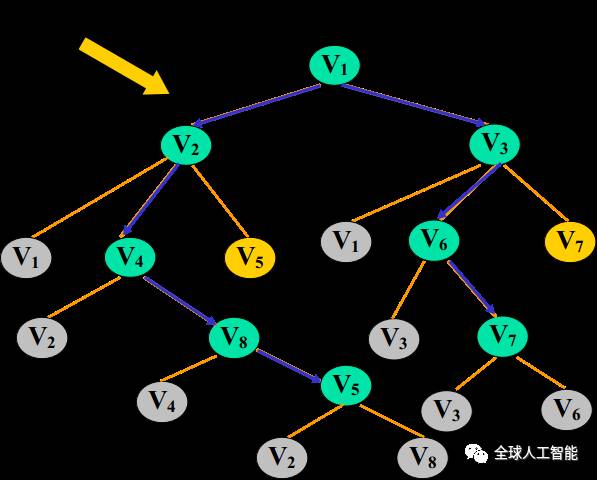
在这里为了区分已经访问过的节点和没有访问过的节点，我们引入一个一维数组bool visited[MaxVnum]用来表示与下标对应的顶点是否被访问过，

流程：
☐ 首先输出 V1，标记V1的flag=true;
☐ 获得V1的邻接边 [V2 V3],取出V2，标记V2的flag=true;
☐ 获得V2的邻接边[V1 V4 V5],过滤掉已经flag的，取出V4，标记V4的flag=true;
☐ 获得V4的邻接边[V2 V8],过滤掉已经flag的，取出V8，标记V8的flag=true;
☐ 获得V8的邻接边[V4 V5],过滤掉已经flag的，取出V5，标记V5的flag=true;
☐ 此时发现V5的所有邻接边都已经被flag了，所以需要回溯。（左边黑色虚线，回溯到V1，回溯就是下层递归结束往回返）
☐
☐ 回溯到V1，在前面取出的是V2，现在取出V3，标记V3的flag=true;
☐ 获得V3的邻接边[V1 V6 V7]，过滤掉已经flag的,取出V6，标记V6的flag=true;
☐ 获得V6的邻接边[V3 V7],过滤掉已经flag的,取出V7，标记V7的flag=true;
☐ 此时发现V7的所有邻接边都已经被flag了，所以需要回溯。（右边黑色虚线，回溯到V1，回溯就是下层递归结束往回返）

深度优先搜索的代码

3.广度优先搜索算法

分析广度优先遍历

所谓广度，就是一层一层的，向下遍历，层层堵截，还是这幅图，我们如果要是广度优先遍历的话，我们的结果是V1 V2 V3 V4 V5 V6 V7 V8。

广度优先搜索的思想：

① 访问顶点vi ；

② 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ；

③ 依次从这些邻接点（在步骤②中访问的顶点）出发，访问它们的所有未被访问的邻接点; 依此类推，直到图中所有访问过的顶点的邻接点都被访问；

说明：

为实现

③，需要保存在步骤②中访问的顶点，而且访问这些顶点的邻接点的顺序为：先保存的顶点，其邻接点先被访问。 这里我们就想到了用标准模板库中的queue队列来实现这种先进现出的服务。

老规矩我们还是走一边流程：

说明：　

☐将V1加入队列，取出V1，并标记为true(即已经访问)，将其邻接点加进入队列，则 <—[V2 V3]　☐取出V2，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V3 V4 V5]

☐取出V3，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V4 V5 V6 V7]

☐取出V4，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V5 V6 V7 V8]

☐取出V5，并标记为true(即已经访问)，因为其邻接点已经加入队列，则 <—[V6 V7 V8]

☐取出V6，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V7 V8]

☐取出V7，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V8]

☐取出V8，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[]

广度优先搜索的代码

两种算法的复杂度分析

深度优先

数组表示：查找所有顶点的所有邻接点所需时间为O(n²)，n为顶点数，算法时间复杂度为O(n²) 　　

广度优先

数组表示：查找每个顶点的邻接点所需时间为O(n²)，n为顶点数，算法的时间复杂度为O(n²)

本文转自博客园 阅读原文点击原文链接

❈

全球人工智能近期经典文章推荐

❈