二分查找的高阶应用实战
Posted 天空的代码世界
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二分查找的高阶应用实战相关的知识,希望对你有一定的参考价值。
以前介绍过二分查找的基础知识,现在来看看高阶应用吧!
一、背景
在上周的文章《》里提到,本来想介绍一下二分查找的基础知识的,结果发现很早之前介绍过《》,就没有冗余介绍了。
后来,发现如果大家只是学习那些基本的二分查找,其实没啥用。
还会产生一种错觉:理论只是太强,没啥实际用处。
今天就给一些二分查找的高阶应用,来感受一下二分查找的魅力吧。
PS:本来计划正常的写文章,结果最近工作上确实很忙。
这段时间一天写一篇文章是不可能了,尽量两天写一篇文章吧,之前构思了两篇纯项目实践相关的技术文章也一直没时间写,这周末看能不能动笔吧。
二、寻找旋转排序数组中的最小值
题意:一个升序的数组进行了循环右移,求查找最小值。
循环右移样例:数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2]。
思路:二分查找的时候,关键是需要判断最小值在mid左边还是右边。
这个可以通过mid和最右边的值来比较。
还是用上面的样例来讲解。
如果mid大于最右边的值,说明mid是4,5,6,7里面的某一个值,最小值肯定在mid的右边。
如果mid小于最右边的值,说明mid是0,1,2里面的某一个值,最小值肯定在mid的左边。
PS:这里暂时忽略等于的情况,实际你们自己考虑吧。
三、寻找两个有序数组的中位数
题意:给两个有序的数组,求中位数。
如果有两个中位数,则求和除2。
思路:这道题可以转化为在[left1, right1]和[left2,right2]区间内,求第k小的数字。
每次求出两个区间的中位数,比如值分别是mid1和mid2,且假设mid1 < mid2。
如果len(mid1) + len(mid2)>=k,那么我们可以确定答案不在[mid2,right2]内,此时k不变。
如果len(mid1) + len(mid2)< k,则可以确定答案肯定不在[left1, mid1]内,此时k = k - len(mid1)。
依靠上面的理论,可以二分最终找到第k小的数字。

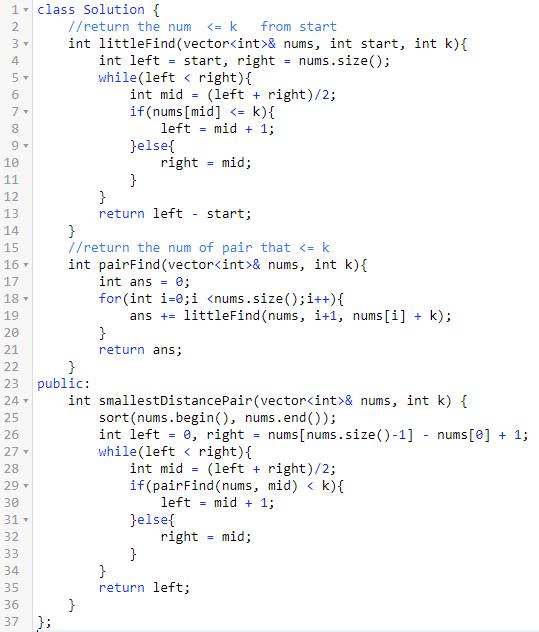
四、找出第 k 小的距离对
题意:给定一个整数数组,返回所有数对之间的第 k 个最小距离。
一对 (A, B) 的距离被定义为 A 和 B 之间的绝对差值。
输入:nums = [1,3,1] k = 1
输出:0
解释:
所有数对如下:
(1,3) -> 2
(1,1) -> 0
(3,1) -> 2
因此第 1 个最小距离的数对是 (1,1),它们之间的距离为 0。
思路:这道题需要先根据样例输入来理解题意。
n个数字,大概会有C(n,2)种差值,求最第k小的差值。
起初看到这道题,我是没有思路的。
想到这道题属于二分专题,我就有思路了。
既然是寻找第k小的差值,我们可以二分差值,判断是否满足有k个。
预先对数组排序,则差值可以划分为n-1组。
(1,2) (1,3) (1,4) ... (1,n)
(2,3) (2,4) ... (2,n)
(3,4) ... (3,n)
...
(n-2,n) (n-1,n)
(n-1,n)
对于每组差值,从左到右是递增的。
所以可以二分判断每组有多少个差值满足要求。
这样就可以求出所有满足差值的个数。
总体复杂度O(n * log(n) * log(n))
五、分割数组的最大值
题意:给一个非负整数组成的数组和一个整数m。
需要将这个数组划分为m个连续的子数组,使得这m个子数组的和的最大值最小。
思路:对于求满足某个规则的最大值最小或者最小值最大,一般都是使用二分搜索。
具体就是二分答案可能所属的区间,判断是否满足条件,直到找到最优的满足条件的答案。
而对于这道题,二分之后,则是给一个最大值K,需要判断是否满足划分,这个一层循环即可判断一个数组是否可以划分为m部分且最大和不超过K。
复杂度O(n * log(sum))。
实际上,如果预处理前缀和或者后缀和,可以再次使用二分来快速找到下一个不超过K的边界,需要找m次。
这样复杂度就是 O(log(sum) * m * log(n)),当然最坏情况下还是 O(n * log(sum))。
五、最后
这里分享了四道二分相关的题,这四道题里除了前两道还算简单(赤裸裸的二分搜索),后两道就不容易想到了。
而实际场景中,都是像后两道题那样,并不是赤裸裸的二分题,而是一个实际问题,需要自己去构造出一个模型然后使用已有的算法去解决。
-EOF-
QQ算法群:165531769(不止算法)
给个好看
一起学习算法
以上是关于二分查找的高阶应用实战的主要内容,如果未能解决你的问题,请参考以下文章